Система показників абсолютного та відносного вимірювання ризику
| Показник | Формула розрахунку | Характеристика | |
| Абсолютне вимірювання ризику | |||
| Абсолютна величина ризику (абсолютний рівень втрат) | 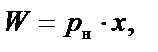 де W — величина ризику, pн — імовірність небажаних наслідків, х — величина цих наслідків
де W — величина ризику, pн — імовірність небажаних наслідків, х — величина цих наслідків
| Перевагою даного підходу є те, що в якості i-го параметра (Pі) можна використовувати широкий спектр показників, за якими підприємство прогнозує збитки у випадку реалізації певного ризику або групи ризиків | |
| Математичне сподівання | Для дискретної величини
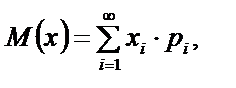 де хі — значення випадкової величини, і = 1, 2,…, рі — відповідні ймовірності.
де хі — значення випадкової величини, і = 1, 2,…, рі — відповідні ймовірності.
| Математичне сподівання, пов’язане з невизначеною ситуацією, є середньо- зваженим усіх можливих результатів, де ймовірність кожного з них використовується як частота або питома вага відповідного значення. | |
Продовження табл. 7.16
| Показник | Формула розрахунку | Характеристика |
Для обмеженого числа (n) можливих значень випадкової величини
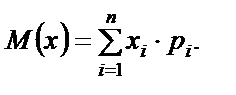 Для випадкової неперервної величини x
Для випадкової неперервної величини x
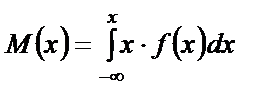 або або
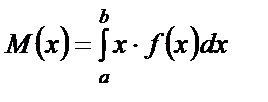 ,
якщо неперервна випадкова величина визначена на інтервалі [a, b], де f(x) — щільність ймовірності ,
якщо неперервна випадкова величина визначена на інтервалі [a, b], де f(x) — щільність ймовірності
| Сподіване значення вимірює результат, котрий середньому очікується. Імовірнісний зміст математичного сподівання конкретного параметра від проведення підприємницької діяльності полягає в тому, що воно приблизно дорівнює середньому арифметичному його можливих значень | |
| Дисперсія | Для випадкової величини X
 Для дискретної випадкової величини Х
Для дискретної випадкової величини Х
 Для неперервної величини Х
Для неперервної величини Х
 або або
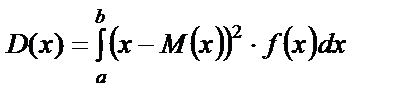
| Дисперсія — середньозважене з квадратів відхилень дійсних результатів від середніх очікуваних. Характеризує розсіювання значення випадкового параметра від його середнього прогнозованого значення |
| Середньоквадратичне відхилення | 
| Показує максимально можливе коливання певного параметра від його се- редньоочікуваної величини та дає можливість оцінити ступінь ризику з погляду ймовірності його здійснення (чим більша величина даної числової характеристики, тим ризикованішим є господарське рішення) |
Продовження табл. 7.16
| Показник | Формула розрахунку | Характеристика | |
Семіваріація
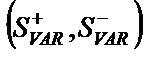
| 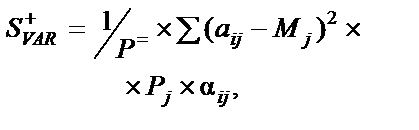 де Р+= — сумарна ймовірність настання тих зовнішньоекономічних умов, які дають ймовірність, більшу від середнього значення
де Р+= — сумарна ймовірність настання тих зовнішньоекономічних умов, які дають ймовірність, більшу від середнього значення
| Додатна семіваріація характеризує дисперсію тих значень прибутку, які більші від середнього. Чим більше значення вона має, тим більшим є очікуваний від варіанту рішення прибуток. Від’ємна семіваріація характеризує дисперсію тих значень прибутку, які менші від середнього. Чим менше від’ємна семіваріація, тим менші очікувані втрати | |
Семіквадратичне відхилення
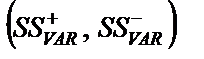
| 
| Додатне семіквадратичне відхилення абсолютного значення сподіваного прибутку; показує абсолютну відстань, на якій знаходиться значення прибутку, більше від середнього (математичного сподівання). Чим більше значення показника, тим більший ризик. Від’ємне семіквадратичне відхилення характеризує відхилення абсолютного значення очікуваних втрат (можливе збільшення втрат). Чим більше значення показника, тим менший ризик | |
| Відносне вимірювання ризику | |||
| Величина ризику у відносному вираженні | Розмір збитків, віднесений до конкретної бази, обраної безпосередньо підприємством, залежно від специфіки та виду оцінюваного ризику | Базою віднесення збитків можуть виступати: витрати на виробництво, вартість основних виробничих фондів, активи підприємства, прибуток, чисельність персоналу, вартість окремих ресурсів і т. д. | |
Закінчення табл. 7.16
| Показник | Формула розрахунку | Характеристика |
| Вибір тієї або іншої бази не має принципового значення, але необхідно віддавати перевагу показнику, що має високий ступінь достовірност | ||
| Коефіцієнт варіації K(х)VAR |  ,
де δ(х) — середньоквадратичне відхилення доходів,
M(x) — величина сподіваних доходів ,
де δ(х) — середньоквадратичне відхилення доходів,
M(x) — величина сподіваних доходів
| Порівнює ризикованість напрямів діяльності і конкретних ситуацій за ознаками (втратами), вираженими у різних одиницях виміру. Коефіцієнт варіації може змінюватися в межах від 0 до 100 %. Чим менша величина, тим більш стабільною є прогнозована ситуація і, відповідно, менший ступінь ризику здійснення напряму діяльності чи певного заходу |
| Коефіцієнт ризику (KR) | 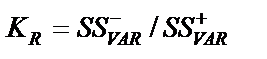
| Чим більше значення, тим більшим є ступінь ризику варіанту рішення |
7.3. Методи кількісного оцінювання
підприємницьких ризиків
Для кількісного визначення ступеня ризику на підприємстві в науковій та спеціальній літературі розглянуто безліч методів оцінювання, але найбільшого практичного застосування набули такі методи, як: статистичний, метод експертних оцінок, метод аналізу доцільності витрат, метод використання ана-
логів.
Статистичний метод використовується за стабільності внутрішнього та зовнішнього середовища діяльності підприємства. Для розрахунку ймовірностей виникнення витрат за даним методом проводиться аналіз статистичної інформації відносно результативності здійснення суб’єктом господарювання певних операцій за відповідний проміжок часу. Імовірність виникнення певного рівня втрат розраховується за формулою:
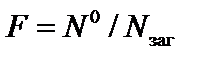 , (7.1)
, (7.1)
де F — імовірність виникнення певного рівня втрат;
N0 — число випадків настання конкретного рівня втрат;
Nзаг — загальна кількість випадків у статистичній вибірці, включаючи й успішні операції даного виду.
Сутність статистичного методу оцінки ризикованих подій базується на теорії ймовірностей розподілу випадкових величин. Маючи достатньо інформації про реалізацію визначених видів ризику в минулих періодах для конкретних видів підприємни-
цької діяльності, суб’єкт господарювання здатен оцінити ймовірність реалізації їх у майбутньому. Ймовірнісно-статистичний підхід передбачає використання як критеріїв таких характеристик випадкової величини, як: математичне сподівання, медіана, дисперсія. Вони визначаються функцією розподілу випадкового збитку, який відповідає розглядуваному ризику. Для розрахунку ступеня певного виду ризику необхідно знати закон його розподілу, тобто знати, за яких умов він може бути реалізований, як його реалізація відображатиметься на діяльності суб’єкта господарювання. Використовуючи описану вище методику, суб’єкти підприємницької діяльності можуть розрахувати ступінь ризику практично для будь-якого напряму діяльності, портфеля інвестицій чи замовлень. Прикладом використання статистичного методу служить оцінка галузевого ризику, або b-ризику, оцінка ризиків клієнта, розрахунок конкурентних ризиків. Статистичний метод дає можливість аналізувати та оцінювати різні «сценарії» реалізації конкретного виду діяльності.
У тих випадках, коли інформація обмежена, для кількісного аналізу ризику використовуються аналітичні методи, або стандартні функції розподілу ймовірностей, наприклад, нормальний розподіл або розподіл Гауса, метод показників (експоненціальний) розподілу ймовірностей, який доволі широко застосовують у теорії масового обслуговування. Ймовірнісна оцінка ризиків математично достатньо розроблена, але спиратися тільки на математичні розрахунки в підприємницькій діяльності не завжди доцільно, оскільки точність розрахунків багато в чому залежить від вихідної інформації.
Експертний метод (метод експертних оцінок) визначення ступеня ризику використовують за браку статистичної інформації в минулому періоді, або коли проводиться оцінка ризиків напряму підприємницької діяльності, що не має аналогів, а це, як правило, також не дає можливості аналізувати минулі показники. Він вважається більш суб’єктивним, порівняно з іншими методами. Експертне оцінювання ймовірності втрат проводиться за таким алгоритмом:
— формування цілей проведення експертної оцінки;
— постановка задачі;
— створення робочої групи для виконання обсягу робіт, передбачених етапами, що зазначені нижче;
— підбір членів експертної групи (керівники, провідні спеціалісти, зовнішні експерти, працівники страхових компаній); оптимальним складом групи експертів для підприємств середніх розмірів є чотири особи; визначення компетентності за формулою:
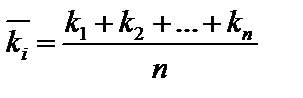 , (7.2)
, (7.2)
де 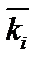 — середній коефіцієнт компетентності i-го експерта;
— середній коефіцієнт компетентності i-го експерта;
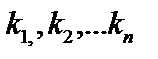 — значення коефіцієнтів компетентності, наданих іншими експертами і-му експерту, включаючи власну оцінку;
— значення коефіцієнтів компетентності, наданих іншими експертами і-му експерту, включаючи власну оцінку;
n — кількість експертів.
Економісти, що займаються подібними питаннями, пропонують використовувати матрицю компетентності (табл. 7.17) [46].
Таблиця 7.17
Дата добавления: 2016-04-22; просмотров: 723;
