Тригонометрическая интерполяция

Поскольку многие явления в природе имеют циклический характер, широкое практическое применение получила интерполяция дискретных периодических функций тригонометрическими полиномами вида:

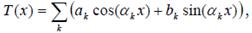
где

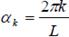- частота k-ой гармоники,

L- период,

a_k, b_k - коэффициенты разложения.

Такой подход позволяет представить сложную циклическую структуру в виде суперпозиции простых периодических функций (элементарных гармоник).

Рассмотрим таблично заданную на периоде Lфункцию y_i(x_i) с равномерным распределением узлов x_i = x₀ + ih,h=L/n , i = 0,…, n.

Тогда, если n - четно (n = 2m), существует единственный интерполяционный тригонометрический полином T_m(x)степениm = n /2, удовлетворяющий условиям T_m(x_i) = y_i, i = 0,…, n:

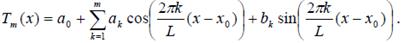
Коэффициенты разложения определяются следующим образом:

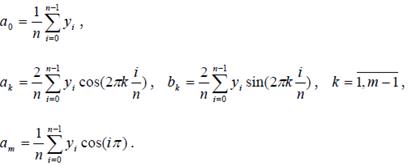
Отметим, что периодичность исходной функции y_i(x_i) предполагает, что y_{0 =} y_n. Если это условие не выполнено, то построенный тригонометрический полином будет удовлетворять условиям интерполяции во всех узлах, кроме последнего, т.е.

T_m(x_i) = y_i, i = 0,…, n – 1.

В последнем узле будет выполняться условие периодичности

T_m(x_n) = T_m(x₀).

КОНТРОЛЬНЫЕ ВОПРОСЫ

Вопрос 1. Когда возникает необходимость в использовании интерполяционных методов?

Вопрос 2. В чём сущность задачи интерполирования?

Вопрос 3. Поясните смысл терминов: интерполяция, экстраполяция и аппроксимация.

Вопрос 4. Как строится интерполяционный многочлен Лагранжа?

Вопрос 5. Как оценивается погрешность интерполяционной формулы Лагранжа?

Вопрос 6. Дайте определение понятий разделенной разности нулевого и первого порядков.

Вопрос 7. Объясните принцип построения интерполяционного полинома Ньютона.

Вопрос 8. В чем разница между глобальной и локальной разновидностями интерполяции?

Вопрос 9. Что такое сплайн-интерполяция?