Сплайн-интерполяция
Рассмотренная в предыдущих разделах вариант интерполяции, когда интерполяционный полином строится сразу по всем узлам интерполяции называется глобальной интерполяцией. При этом увеличение числа узлов автоматически приводит к повышению степени полинома, и как следствие, к проявлению его колебательных свойств (рис.8.2).
Поэтому обычно полиномиальную интерполяцию осуществляют максимум по 3-4 узлам. Интерполяцию по нескольким узлам табл. 8.1, называют локальной.
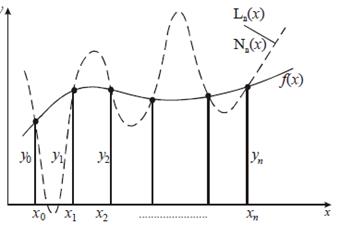
Рис. 8.2. Проявление колебательных свойств глобального интерполяционного полинома при большом числе узлов
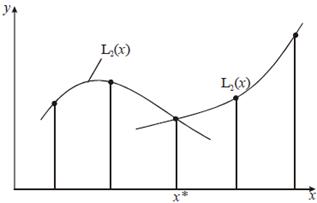
Рис. 8.3. Иллюстрация варианта локальной интерполяции по каждым трем узлам
Однако, такая локальная интерполяция с помощью полиномов Lnили Nnстрадает тем недостатком, что интерполирующая функция в узлах стыковки полиномов имеет непрерывность только нулевого порядка, т.е. интерполирующая функция принадлежит классу функций C0 (см. рис. 8.3 для Lnи Nn в узле x*).
От этих недостатков свободна сплайн-интерполяция, которая требует непрерывности в узлах стыковки локальных многочленов по производным соответственно порядка один, два, и т.д.
Определение. Сплайном - степени mдефекта r называется (m - r)раз непрерывно дифференцируемая функция, которая на каждом отрезке [xi – xi-1], i = 1,…, n представляет собой многочлен степени m.
В науке и технике наиболее распространены сплайны 3-й степени дефекта один, т.е.
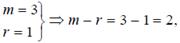
т.е. дважды непрерывно дифференцируемый многочлен 3-й степени на каждом отрезке [xi , xi-1], i = 1,…, n. Сплайны, удовлетворяющие условию интерполяции, называются интерполяционными.
Основным достоинством интерполяционного кубического сплайна дефекта один является следующее: этот сплайн обладает минимумом интегральной кривизны на всем заданном отрезке [a, b] по сравнению с другими интерполяционными функциями f *(x), т.е.
.
Геометрически это означает, что если тяжелую упругую нить повесить на ряд гвоздей, то она примет форму кубического сплайна дефекта 1, приведенную на рис. 8.4.
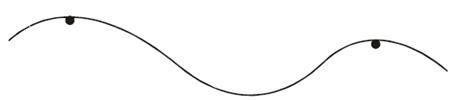
Рис. 8.4. Тяжелая упругая нить, геометрически представляющая собой кубические сплайны дефекта один
Рассмотрим алгоритм построения интерполяционного кубического сплайна S(x), i =1,…, n дефекта один в соответствии с табл. 8.2. Кубический полином Si(x) на отрезке [xi-1 , xi] имеет четыре неизвестных коэффициента. Количество отрезков в соответствии с табл. 8.2 равно n. Для определения 4×n коэффициентов можно использовать следующие условия в узлах интерполяции:
· условие интерполяции
S(xi) = yiдля i =1,…, n
· непрерывность сплайна
S(xi - 0) = S(xi + 0)для i =1,…, n-1
· непрерывность производных 1-го порядка
S’(xi - 0) = S’(xi + 0)для i =1,…, n-1
· непрерывность производных 2-го порядка
S”(xi - 0) = S”(xi + 0)для i =1,…, n-1
Таким образом, всего имеется (n+1) + 3(n-1) = 4n - 2условий. В качестве двух недостающих условий задают значения производных 1-го или 2-го порядка в узлах x0 и xn. Для вывода используем значения S”(x0) = S”(xn). В этом случае сплайн называется естественным.
Пусть S”(x) = q(x). Рассмотрим поведение функции q(x) на отрезке [xi-1 , xi] (см. рис. 8.5).
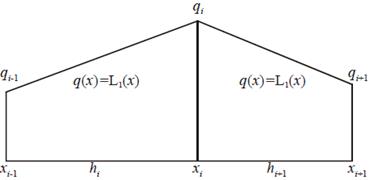
Рис. 8.5. Поведение функций S”(x) на элементарных отрезках
Поскольку сплайн является многочленом 3-й степени, то на каждом отрезке [xi-1 , xi], 2-я производная будет линейна. Найдем ее с помощью интерполяционного многочлена Лагранжа 1-й степени L1(x):
(8.18)
Выражение (8.18) уже удовлетворяет условиям непрерывности производных 2-го порядка. Действительно, подставим в (8.18) x = xi − 0, получим q(xi − 0) = qi.
Затем, записывая выражение (8.18) для отрезка xÎ[xi , xi+1]
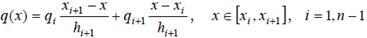
и подставляя в него xi + 0 вместо x, получим q(xi + 0) = qi, что и требовалось показать.
Для нахождения сплайна проинтегрируем дважды выражение (8.12), получим
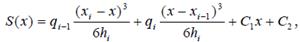(8.19)
где C1и C2найдем из удовлетворения значений сплайна (8.19) в узлах xi-1, xi условиям интерполяции
.
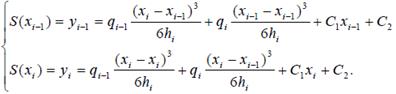Решая эту СЛАУ относительно C1и C2и подставляя их в (8.19), найдем следующее выражение для сплайна степени 3 дефекта 1:
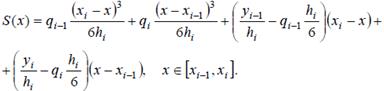(8.20)
В этом сплайне узловые значения для вторых производных qi пока неизвестны. Будем искать их из условий непрерывности первых производных в узлах xi.
Для нахождения производной S′(xi + 0) запишем (8.20) для отрезка [xi , xi+1]
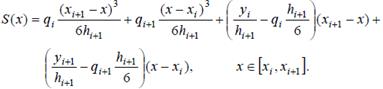(8.21)
Вычисляя из (8.20) и (8.21) производные первого порядка и подставляя в них значение x = xi, получим
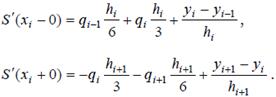
Приравняем эти выражения в соответствии с условиями непрерывности первых производных в узлах интерполяции xi, получим
(8.22)
q0 = qn = 0. (8.23)
Система (8.22) с заданными краевыми условиями (8.23) представляет собой СЛАУ относительно qi = S’’(xi), i = 1,…, n -1, имеет трехдиагональную матрицу и, следовательно, ее можно решать методом прогонки. Подставляя найденные qi,i = 0,…, n, в (8.21), получим кубические сплайны дефекта один на каждом отрезке xÎ[xi , xi+1], i = 1,…, n.
Таким образом, определяющими выражениями для определения кубических сплайнов дефекта один являются выражения (8.21), (8.22), (8.23).
Пример 8.4.Для заданной таблицы с шагом h = xi - xi-1 = 1 = const построить интерполяционный кубический сплайн дефекта один, выписав соответствующие уравнения на каждом отрезке xÎ[xi-1 , xi], i = 1,…, 4. Проверить непрерывность сплайна и его производных до второго порядка включительно в узле x* = 2.
Р е ш е н и е
Под заданной таблицей сформируем дополнительную строку для вторых производных сплайнов S’’(xi)≡ qi , которая заполняется по мере их вычисления (сразу можно вписать в нее q0 = q4 = 0).
Для узлов x1= 2; x2 = 3; x3 = 4с учетом q0 = q4 = 0 составляется СЛАУ (8.22) относительно неизвестных q1, q2, q3.
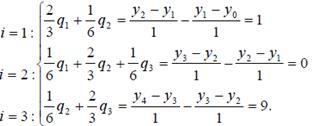
Прогоночные коэффициенты вычисляются по формулам
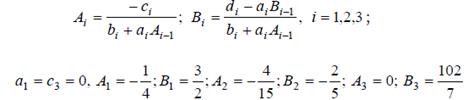
и значения
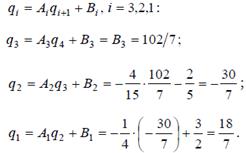
Заносим эти значения в дополнительную строку таблицы и для каждого из четырех интервалов выписываем уравнения сплайна (8.12).
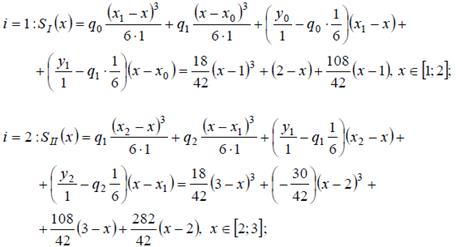
Проверим правильность построения сплайна для узла x* = 2. К данному узлу примыкают кривые S1(x) и S2(x).
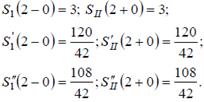
Дата добавления: 2016-04-22; просмотров: 2875;