Погрешность полиномиальной интерполяции

Ясно, что в узлах интерполяции погрешность интерполяционного полинома L_n(x)или N_n (x)равна нулю, т.е.

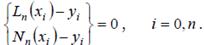
Погрешность L_n(x) - f(x) представляющая собой разность между значением интерполяционного многочлена L_n(x)и значением функции f(x) в точке x, не совпадающей с узлом интерполяции имеет вид:

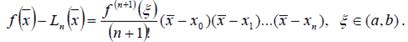(8.15)

Где 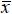- точка, в которой ищется погрешность (не совпадает с узлами интерполяции).

Поскольку точка ξÎ(a,b) неизвестна, то вместо погрешности, определяемой выражением (8.15) вводится верхняя оценка погрешности в виде

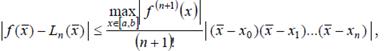(8.16)

которая обычно используется на практике.

Таким образом, погрешность интерполяции зависит как от величины соответствующей производной приближаемой функции, так и от расположения узлов. Минимизировать погрешность приближения достаточно гладкой функции на отрезке [a,b] полиномом можно, расположив узлы интерполяции следующим образом:

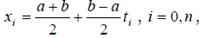
где

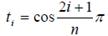- корни полинома Чебышева

H_n (x) = cos(n arccos(x))

или в рекуррентном виде

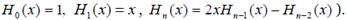
Отметим также, что такое расположение узлов интерполяции гарантирует сходимость интерполяционного полинома к приближаемой функции при повышении числа узла интерполяции (степени полинома), тогда как при равномерном распределении узлов в ряде случаев может наблюдаться расходимость (такая ситуация хорошо иллюстрируется известным примером Рунге, в котором функция

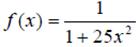
приближается интерполяционным полиномом на отрезке [-1,1]).

Пример 8.2.Построить интерполяционный полином Лагранжа, совпадающий с функцией f(x) = 3^x, xÎ[-1,1]в точках x₀ = -1, x₁ = 0, x₂ = 1. Вычислить значение сеточной функции и оценить погрешность интерполяции в точке x^* = 5,0.

Р е ш е н и е

Составим сеточную функцию и занесем ее в таблицу. Поскольку n=2, то необходимо построить интерполяционный полином L₂(x).

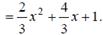(8.17)

Проверим условия интерполяции

L₂(-1) = 1/3; L₂(0) = 1; L₂(1) = 3.

Значение сеточной функции в точке x^* = 0,5 вычислим по интерполяционному многочлену (8.17)

y(0,5) = L₂(0,5) = 1,8333.

Верхнюю оценку погрешности интерполяционного многочлена определим в соответствии с выражением (8.16)

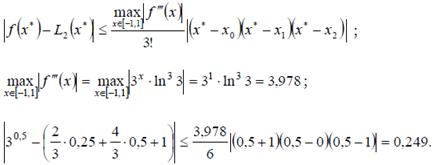
Поскольку функция f(x) = 3^x известна, то можно вычислить точное значение абсолютной погрешности в точке x^*= 0,5.

Пример 8.3.Составить интерполяционный полином Ньютона для заданной таблицы

Р е ш е н и е

Таблица задана с неравномерным шагом, поэтому для решения задачи воспользуемся многочленом Ньютона с разделенными разностями (8.14)

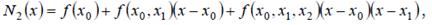
где

f(x₀) = y₀ = 1/3;

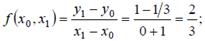
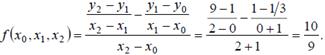
Таким образом,

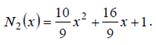
Условия интерполяции соблюдены:

N₂(-1) = 1/3; N₂(0) = 1; N₂(2) = 9.