Территориальные индексы

Территориальные индексы применяются для пространственных, межрегиональных сопоставлений различных показателей. Их расчет более сложен, чем расчет традиционных (динамических) индексов, рассмотренных ранее, по следующим причинам:

1) различия в структуре цен и количества товаров между странами гораздо значительнее, чем между периодами в рамках одной страны, что обусловлено особенностями экономики разных стран.

2) территориальные (международные) сопоставления нередко осуществляются одновременно для группы стран (например, стран ЕС или СНГ), поэтому необходимо согласовывать индексы, исчисленные для всей группы стран.

Для исчисления территориальных индексов применяются особые формулы, которые разработаны на основе положений двух теорий индексов: аксиоматической и экономической.

В аксиоматической теории индексов сформулирован ряд требований к индексам с точки зрения формальной логики (например, требования факторной пробы, обратимости во времени, тождественности и др.) Так, требование тождественности означает, что если цены в отчетном периоде не изменились по сравнению с ценами в базисном периоде, то общий индекс цен должен быть равен единице независимо от изменения физического объема. Другое требование этой теории ­­­­– пропорциональность индексов…

В экономической теории индексов содержится концептуальная основа для поиска «истинного» индекса. Так, истинный индекс цен можно получить, сопоставив расходы потребителей в текущем и базисном периодах при условии, что они обеспечивают равную полезность потребителям при разных ценах, т.е. фактические расходы потребителей сравниваются с условными, гипотетическими, которые при разных ценах в двух периодах обеспечивают одинаковую полезность. Это сравнение и должно обеспечить отыскание «истинного» индекса цен. Заметим, что экономическая теория индексов достаточно абстрактна, поскольку статистики не оперируют категорией полезности, а имеют дело с конкретными товарами и услугами. Тем не менее, теория выражает некий общий теоретический подход к разработке индексов.

В специальной литературе не прекращается дискуссия об обоснованности аксиоматической и экономической теорий индексов и о возможности применения положений этих теорий в статистической практике. Аксиоматическую теорию критикуют за то, что в ней предполагается отсутствие связи между изменением цен и изменением физического объема. Экономическую теорию критикуют за абстрактный характер, то есть за то, что невозможно использовать ее выводы в практической деятельности.

Основные требования к территориальным индексам:

1. Характерность весов, то есть для показателей двух стран А и Б в качестве весов должны использоваться цены (физический объем) этих стран А и Б (или средние из них), а не цены (физический объем) какой-либо третьей страны.

2. Независимость от выбора базисной страны (требование обратимости индексов во времени, адаптированное к территориальным сопоставлениям), то есть

I^А/Б I^Б/А = 1, (212)

где I^А/Б – индекс цен (физического объема) страны А по отношению к стране Б;

I^Б/А – индекс цен (физического объема) страны Б по отношению к стране А.

3. Транзитивность, то есть

I^А/Б = I^А/В : I^Б/В, (213)

где I^А/В – индекс цен (физического объема) страны А по отношению к стране В;

I^Б/В – индекс цен (физического объема) страны Б по отношению к стране В.

Суть требования транзитивности состоит в том, что индекс, полученный для некоторой пары стран А и Б путем прямого сопоставления их цен (физического объема), должен быть равен этому же индексу, полученному косвенным путем, то есть делением индекса I^А/В на индекс I^Б/В.

4. Аддитивность, то есть индексы цен (физического объема), рассчитанные для всей совокупности товаров и услуг, должны быть четко согласованы с индексами, исчисленными для всех групп этой совокупности.

5. Требование факторной пробы, то есть произведение индекса цен и индекса физического объема должно быть равно индексу стоимости:

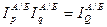. (214)

В теории и практике международных сопоставлений различают прямые парные и многосторонние сопоставления. Каждые имеют свою специфику, поэтому для их проведения используют различные формулы индексов.

Прямые парные сопоставления проводятся для какой-либо изолированной пары стран (например, для России и США), на которые не влияют показатели третьих стран. Для таких сопоставлений важным является требование характерности весов, факторной пробы и независимости от выбора базисной страны.

Многосторонние сопоставления проводятся одновременно для группы стран, поэтому особое значение приобретает требование транзитивности индексов.

Например, прямые парные сопоставления ВВП и паритетов покупательной способности (ППС) валют проводят в 4 этапа:

1) ВВП сопоставляемых стран А и Б подразделяется на однородные товарные группы (как правило, около 300 групп);

2) для каждой товарной группы подбирается несколько идентичных товаров-представителей с ценами, что дает возможность вычислить индивидуальные индексы цен для всех отобранных товаров-представителей (i₁, i₂, i₃, …, i_n);

3) для каждой товарной группы по индивидуальным индексам цен на товары-представители исчисляется средний индекс цен по формуле средней геометрической простой:

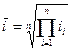, (215)

что связано с необходимостью обеспечить независимость индексов от выбора базисной страны (формула средней арифметической не обеспечивает этого требования) и с практическим отсутствием информации о весах товаров-представителей;

4) рассчитываются средние индексы цен (физического объема) для ВВП в целом по формулам Ласпейреса (199) и Пааше (201), в которых в качестве весов Q используются доли отдельных товарных групп в ВВП:

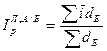, (216) 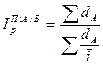; (217)

5) рассчитывается средний индекс цен (физического объема) по формуле Фишера (193);

6) определяется индекс физического объема ВВП стран А и Б путем делением индекса стоимости ВВП этих стран на средний индекс цен Фишера.

Еще один способ прямого парного сопоставления ВВП – это последовательно сопоставить ВВП двух стран А и Б соответственно в ценах стран А и Б, при этом получим 2 индекса физического объема по формулам Ласпейреса (186) и Пааше (188) и исчислить средний индекс физического объема по формуле Фишера (192).

Для проведения многосторонних сопоставлений ВВП и ППС разработаны формулы индексов, которые удовлетворяют требованию транзитивности: формулы ЭКШ, Гири-Камиса, Уолша и Джерарди.

Чаще других используется формула ЭКШ[61], которая представляет собой среднюю геометрическую из индексов Фишера для любой пары сравниваемых стран А и Б, исчисленных косвенным путем, т.е. через третью страну j:

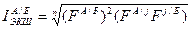, (218)

где 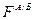– индекс Фишера для стран А и Б; 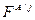– индекс Фишера для стран А и j; 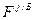– индекс Фишера для стран j и Б; n – число стран, участвующих в сопоставлении.

Недостатком формулы (218) является то, что она не удовлетворяет требованию аддитивности. Этого недостатка нет у формулы Гири-Камиса.

Формула Гири-Камиса позволяет исчислять средние международные цены на различные группы товаров, выраженные в единицах условной международной валюты, а также ППС валют всех стран, участвующих в многосторонних сопоставлениях, по отношению друг к другу и к условной международной валюте:

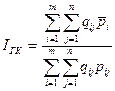, (219)

где q_ij– количество i-го товара в j-ой стране; p_ij– цена i-го товара в j-ой стране; 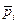– международная цена i-го товара.

Недостатком формулы (219) является то, что она не удовлетворяет требованию характерности весов.

Еще один метод территориальных сопоставлений, для которого разработана особая форма индекса, носит название метода Уолша, формула которого имеет следующий вид:

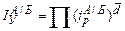, (220)

где 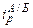– средний индекс цен для i-ой товарной группы в стране А по сравнению со страной Б; – средняя доля i-ой товарной группы для всей совокупности стран, принимающих участие в сопоставлении.

По формуле (220) рассчитывается средний геометрический индекс, взвешенный по средним весам для группы стран, участвующих в сопоставлении; в качестве этих средних весов выступают средние (для всей совокупности стран) доли товарных групп в соответствующих показателях (например, в ВВП). Формула (220) удовлетворяет требованиям транзитивности и независимости от выбора базисной страны, но не удовлетворяет требованию аддитивности, а также в меньшей мере, чем индексы ЭКШ, удовлетворяет требованию характерности весов.

В практике международных сопоставлений ВВП, проводимых в рамках ЕС, в течение нескольких лет применялся метод Джирарди, в основе которого лежит исчисление индексов физического объема ВВП различных стран с помощью оценки ВВП в средних международных ценах, получаемых по формуле средней геометрической простой. Этот метод похож на метод Гири-Камиса, однако, в отличие от него средние международные цены исчисляются здесь по формуле средней геометрической простой (а не по формуле средней арифметической взвешенной, как в методе Гири-Камиса).

При территориальном сопоставлении макроэкономических показателей широко применяется также метод цепных индексов, когда в рамках некоторой группы стран интересующий показатель (например, ВВП) сравнивается с этим показателем какой-либо одной базисной страны, тогда анализируемые показатели каждой из этой группы стран, кроме базисной, сравниваются с помощью цепных индексов, то есть по отношению к базисной стране.

[1] От лат. status – состояние, положение вещей; первоначально термин употреблялся в значении «политическое состояние»

[2] Эту деятельность на профессиональном уровне осуществляет государственная статистика – Федеральная служба государственной статистики (ФСГС) и система ее учреждений, организованных по административно-территориальному признаку, а также ведомственная статистика (на предприятиях, ведомствах, министерствах и т.д.). Информация ФСГС публикуется в специадльных печатных изданиях, а также в сети Интернет: www.gks.ru (или www.fsgs.ru)

[3] Термин «статистика» как параметр, как статистический критерий употребляется преимущественно в математической статистике, некоторые из них (χ², t и др.) рассмотрены в соответствующих темах данного курса лекций

[4] «There are three types of lies - lies, damn lies, and statistics» (Benjamin Disraeli, 1804 – 1881)

[5] « As a general rule, the most successful man in life is the man who has the best information »

[6] Аналогично общее количество школьных тетрадей измеряется в у.ш.т.(условные школьные тетради размером 12 листов), продукция кон­сервного производства измеряется в у.к.б. (условные консервные бан­ки емкостью 1/3 литра или 400 грамм); продукция моющих средств приво­дится к условной жирности 40%

[7] f – это начальная буква англ. слова frequency – частота

[8] В статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)

[9] Во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения»

[10] Часто встречается и другое название темпа изменения – темп прироста, что не совсем логично (см. предыдущую сноску)

[11] Обычно (в т.ч. и в дальнейшем в данном пособии) в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N-ю (последнюю)

[12] Для взвешенной средней сумма взвешенных отклонений равна нулю – доказать самостоятельно

[13] Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h

[14] Единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается

[15] От греч. «гистос» – ткань, строение

[16] От греч. слов «поли» и «гонос» – многоугольник

[17] При четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант

[18] Получите формулы и произведите их расчет (по аналогии с формулами для расчета квартилей) самостоятельно

[19] Максимально возможные значения показателей вариации: Л_max = ; ; ;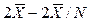

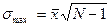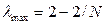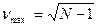
[20] Например, цена продажи американского доллара в коммерческих банках Н.Новгорода 26 июля 2007 года варьировала от 25,45 до 26,00 при средней цене 25,595 руб., тогда по формуле (32) 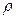= (26,00–25,45)/25,595 = 0,021, или 2,1%. Такая малая вариация вызвана тем, что при значительном различии курса доллара немедленно произошел бы отлив покупателей из «дорогого» банка в более «дешевые». Напротив, цена килограмма говядины в разных регионах России варьирует очень сильно – на десятки процентов и более. Это объясняется разными затратами на доставку товара из региона-производителя в регион потребитель.

[21] Прочие виды распределений изучаются дисциплиной «Теория вероятностей»

[22] Простой расчет возможен при наличии Excel из пакета Microsoft Office, где имеется функция, вычисляющая плотность (или интеграл) функции нормального распределения =НОРМРАСП(А;Б;В;Г), где параметры: А – значение X; Б – средняя арифметическая 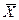; В – среднее квадратическое отклонение σ; Г – «0» для вычисления плотности (или «1» для вычисления интеграла) распределения

[23] Иногда за счет округлений при расчетах (использование функции плотности распределения вместо интеграла) может быть нарушено равенство сумм эмпирических и теоретических частот, что и произошло в нашем примере про ВО (∑f=35, ∑m=33,832)

[24] Практически приемлемая вероятность в экономических исследованиях, означающая, что в 5 случаях из 100 может быть отвергнута правильная гипотеза

[25] Основное условие для использования критерия Колмогорова – достаточно большое число наблюдений (N > 50)

[26] Названо по имени французского математика Симеона Пуассона (1781 – 1840), еще называют законом распределения редких явлений; возникает, когда значения признака выражены дискретно и являются результатом какого-либо редко возникающего события среди наблюдаемых единиц, причем с увеличением значений признака вероятность наступления события падает

[27] Важно не путать понятие «структурный сдвиг», оцениваемый в теме 8, где он представляет не величину самого изменения структуры, а его влияние на результативный показатель

[28] Индекс не удовлетовряет свойству независимости от раскола совокупности

[29] Существуют и другие показатели, о которых можно прочитать в специальной литературе

[30] Приведены наиболее простые функции, более сложные виды, такие как логарифмическая, логистическая и др. описаны в специальной литературе, например – [2]

[31] При расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»

[32] Понятие «уровень значимости» описано ранее на стр. 29

[33] Выравнивание по параболе рассмотрено в методических указаниях к теме на другом примере

[34] Используется при малом количестве уровней (n<30), в противном случае (n>30) вместо 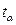используют коэффициент доверия t нормального закона распределения (Приложение 1)

[35] Попробуйте проделать данное задание самостоятельно (в случае затруднений обратитесь к методическим указаниям по данной теме)

[36] Выполните это задание дома самостоятельно (подсказка: продифференцировав и приравняв нулю уравнение учтите, что 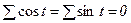и )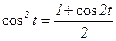

[37] Подобрать уравнение второй гармоники ряда Фурье по данным табл. 32 самостоятельно

[38] Проделайте данное задание самостоятельно

[39] Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо

[40] Термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака

[41] Термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного

[42] Множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция

[43] При измерении тесноты связи между рядами динамики это равнозначно отсутствию автокорреляции между уровнями ряда, т.е. прежде чем оценивать тесноту связи между рядами динамики, необходимо проверить каждый ряд на автокорреляцию – см. методические указания

[44] Проделать это самостоятельно

[45] Термин «регрессия» ввел в статистику Ф. Гальтон, который изучив большое число семей, установил, что в группе семей высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов, т.е. отклонение роста от среднего в следующем поколении уменьшается – регрессирует

[46] Параметры a₀ и a₁ можно получить не только методом подстановки как приводится далее, но и методом определителей 2-го порядка (проделать данное задание самостоятельно)

[47] Сумма эмпирических (2864,09) и выравненных по прямой линии (2864,115) значений должна совпадать, но в нашем случае этого не происходит из-за округлений расчетов до 3-х знаков после запятой

[48] В числителе – сумма последнего столбца, а в знаменателе – сумма предпоследнего столбца таблицы 45

[49] Коэффициент автокорреляции можно рассчитывать либо между соседними уровнями, либо между уровнями, сдвинутыми на другое число единиц времени (временной лаг) m; приведенные формулы с временным лагом m=1 (между соседними уровнями) являются самыми распространенными

[50] Формула (156) является тождественной формуле (155)

[51] См. тему 5 «Ряды динамики», метод аналитического выравнивания

[52] Остаточные величины обычно обозначают ε_t, но для того, чтобы различать их для разных рядов динамики x и y, приняты обозначения d_x и d_y

[53] По значению коэффициент контингенции всегда меньше коэффициента ассоциации

[54] Такая очередность изменения факторов (то есть 1-ый – экстенсивный, а 2-ой – интенсивный) применяется по умолчанию тогда, когда ее затруднительно точно установить

[55] В случае построения многофакторных мультипликативных индексных моделей бывает сложно точно определить очередность влияния факторов на результативный показатель, поэтому можно рекомендовать ставить на 1-ое место индекс того фактора, который сильнее всего изменился, на 2-ое место – индекс того фактора, который изменился слабее первого, но сильнее остальных и так далее в порядке убывания изменений индексов

[56] Самостоятельно догадайтесь и придумайте пример, когда эффект Гершенкрона выполняться не будет (подсказка – «эффект картошки»)

[57] Если зафиксировать веса на уровне базисного периода f₀, то получим менее распространенную формулу индекса фиксированного состава: 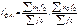или .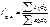

[58] При фиксировании индексируемой величины на уровне отчетного периода x₀ получается менее распространенная формула индекса структурных сдвигов: 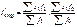или .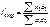

[59] В противном случае применяются формулы, приведенные в сносках к этим формулам. Для определения очередности влияния факторов рассчитываются и те, и другие формулы, а затем рассчитывается их средняя геометрическая величина (индексы Фишера). Сравнивая значения этих индексов Фишера, решается вопрос об очередности влияния факторов: какой из индексов показывает большее изменение, тот фактор и считают 1-ым.

[60] Выбор этой формулы вызван тем, что изменение структуры – это 1-ый фактор, и изменение самих цен – 2-ой (доказать это самостоятельно, воспользовавшись предыдущей сноской)

[61] В названии использованы начальные буквы фамилий трех статистиков, предложивших этот индекс: венгров Элтетэ и Кэвеша и поляка Шульца