Метод центру тяжіння композиції максимум-мінімум
Як повинне змінитися нечітке логічне виведення, якщо А/ задається не як конкретне значення, в як нечітка множина (наприклад, якщо у вище приведеному прикладі відомо, що „студент проводить у бібліотеці середню кількість часу”)? Для цього використовують відношення нечіткої імплікації:
Нечітким відношенням між множинами А та В називається нечітка підмножина їх декартового добутку. Тобто, якщо
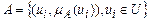 ,
, 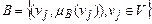 ,
,
то відношення А R В визначається як множина пар
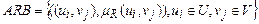 .
.
Відношення нечіткої імплікації А→В можна виводити по різному. Часто використовується формула min-імплікації:
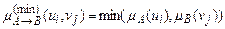 .
.
Для задання імплікації задають також й інші формули:
1) нечітке розширення класичної імплікації:
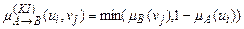 ;
;
2) нечітка імплікація Лукашевича:
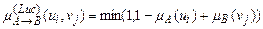 ;
;
Тепер ми можемо отримати множину В/ - нечітку множину висновків, які відповідають множині А/. Це є результатом композиції множини А/ й нечіткої імплікації:
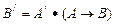
де 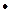 – знак композиції, що обчислюється за формулою
– знак композиції, що обчислюється за формулою
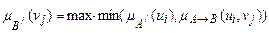 .
.
Але отримати лише множину В/ недостатньо, треба ще знайти конкретну числову відповідь (провести дефадзифікацію). Найчастіше за числову відповідь береться центр тяжіння знайденої нечіткої множини, який обчислюється за формулою
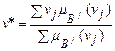 .
.
Увесь описаний метод нечіткого логічного виведення часто називають методом центру тяжіння композиції максимум-мінімум.
Повернемося до попереднього прикладу.
Ми задали функції належності для нечітких множин А („багато працює в бібліотеці”) таВ („високий рейтинг”) таким чином:
А={(3, 0); (6, 0.1); (9, 0.4); (12, 0.6); (18, 0.8); (21, 1); (27, 1)}
В={(59, 0); (72, 0.2); (84, 0.4); (91, 0.7); (96, 0.9); (100, 1)}
Нехай дано, що „студент працює в бібліотеці середню кількість часу”. Задамо нечітку множину А/ (середня кількість часу):
A/={(3, 0); (6, 0.2); (9, 0.7); (12, 1); (18, 0.6); (21, 0.2); (27, 0)}
Обчислимо відношення імплікації нечітких множин А та В:
| А/В | 0.2 | 0.4 | 0.7 | 0.9 | |||
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| 0.4 | 0.2 | 0.4 | 0.4 | 0.4 | 0.4 | ||
| 0.6 | 0.2 | 0.4 | 0.6 | 0.6 | 0.6 | ||
| 0.8 | 0.2 | 0.4 | 0.7 | 0.8 | 0.8 | ||
| 0.2 | 0.4 | 0.7 | 0.9 | ||||
| 0.2 | 0.4 | 0.7 | 0.9 |
Знайдемо композицію множини А/ та знайденого відношення А→В. Результатом буде нечітка множина В/:
| А/В | 0.2 | 0.4 | 0.7 | 0.9 | |||
| 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| 0.7 | 0.2 | 0.4 | 0.4 | 0.4 | 0.4 | ||
| 1.0 | 0.2 | 0.4 | 0.6 | 0.6 | 0.6 | ||
| 0.6 | 0.2 | 0.4 | 0.6 | 0.6 | 0.6 | ||
| 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | ||
| B/ | 0.2 | 0.4 | 0.6 | 0.6 | 0.6 |
Нарешті, проведемо дефадзифікацію отриманої множини В/:
v*=(72∙0.2 + 84∙0.4 + 91∙0.6 + 96∙0.6 + 100∙0.6)/(0.2 + 0.4 + 0.6 + 0.6 + 0.6) = 220.2/2.4 = 91.75 ≈92.
Отже, на основі проведеного розрахунку із застосуванням нечіткого композиційного правила виведення можна дійти висновку, що студент повинен отримати оцінку 92 бали.
Дата добавления: 2016-04-19; просмотров: 993;
