Функции нескольких переменных. Кратные интегралы. Теория поля.
Основные теоретические сведения
1. Частной производной первого порядка функции двух переменных 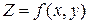 по аргументу
по аргументу 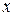 называется предел
называется предел
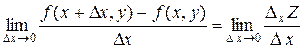 .
.
Обозначение: 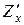 ,
, 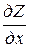 . Нахождение
. Нахождение 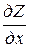 сводится к дифференцированию функции одной переменной
сводится к дифференцированию функции одной переменной 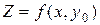 , полученной при фиксировании аргумента
, полученной при фиксировании аргумента 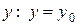
2. Скалярным полем 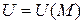 называется скалярная функция точки
называется скалярная функция точки 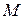 вместе с областью ее определения.
вместе с областью ее определения.
Скалярное поле 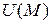 характеризуется градиентом
характеризуется градиентом
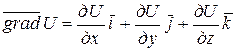
и производной по направлению 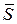 :
:
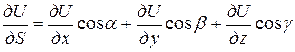 ,
,
где 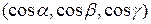 – координаты единичного вектора направления
– координаты единичного вектора направления 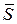 .
.
3. Вычисление двойного интеграла от функции 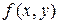 , определенной в области
, определенной в области 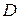 , сводится к вычислению двукратного интеграла вида
, сводится к вычислению двукратного интеграла вида
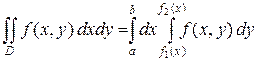 , (1)
, (1)
где область 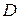 определяется условиями
определяется условиями 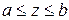 ,
, 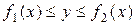 или вида
или вида
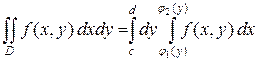 , (2)
, (2)
если область 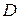 определяется условиями
определяется условиями 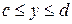 ,
, 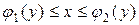 .
.
Переход от равенства (1) к (2) или обратно называется изменением порядка интегрирования.
4. Векторным полем 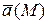 называется векторная функция точки
называется векторная функция точки 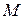 :
:
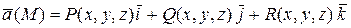 .
.
Векторное поле 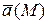 характеризуется скалярной величиной – дивергенцией:
характеризуется скалярной величиной – дивергенцией:
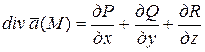
и векторной величиной – ротором:
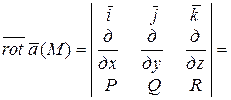
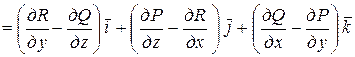 .
.
Векторное поле 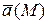 называется соленоидальным, если в каждой точке этой области
называется соленоидальным, если в каждой точке этой области 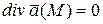 .
.
Векторное поле 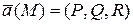 называется потенциальным в области
называется потенциальным в области 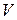 , если в каждой этой области
, если в каждой этой области 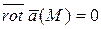 .
.
Для потенциального векторного поля 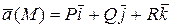 справедлива формула для нахождения потенциальной функции
справедлива формула для нахождения потенциальной функции
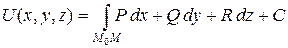 ,
,
где 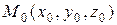 – фиксированная точка области
– фиксированная точка области 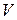 ,
, 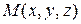 – любая точка области
– любая точка области 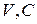 – произвольная постоянная.
– произвольная постоянная.
Потоком 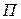 векторного поля
векторного поля 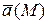 через двустороннюю поверхность
через двустороннюю поверхность 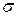 называется поверхностный интеграл
называется поверхностный интеграл
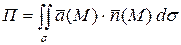 , (3)
, (3)
где 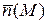 – единичный вектор нормали вдоль
– единичный вектор нормали вдоль 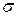 ,
, 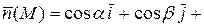
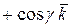 . Если поверхность
. Если поверхность 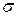 задается уравнением
задается уравнением 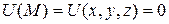 , то
, то
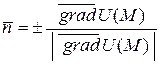 ,
,
причем знак в правой части берется так, чтобы получить нормальный вектор 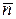 к выбранной стороне поверхности.
к выбранной стороне поверхности.
Для вычисления интеграла (3) удобно проектировать поверхность 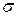 на одну из координатных плоскостей. Пусть, например,
на одну из координатных плоскостей. Пусть, например, 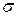 взаимно однозначно проектируется на
взаимно однозначно проектируется на 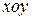 , тогда
, тогда
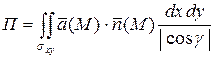 .
.
Если 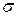 взаимно однозначно проектируется на
взаимно однозначно проектируется на 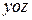 или
или 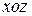 , то
, то
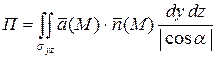 или
или 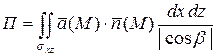 .
.
Иногда вычисление потока проводят методом проектирования 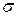 на все три координатные плоскости :
на все три координатные плоскости :
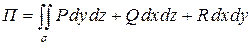 ,
,
каждое слагаемое вычисляется отдельно посредством проектирования 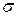 на соответствующую координатную плоскость.
на соответствующую координатную плоскость.
Формула Остроградского устанавливает связь между потоком векторного поля 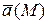 через замкнутую поверхность
через замкнутую поверхность 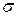 и дивергенцию поля :
и дивергенцию поля :
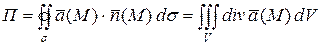 .
.
5. Циркуляция векторного поля 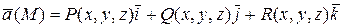 по замкнутой кривой
по замкнутой кривой 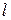 называется криволинейный интеграл
называется криволинейный интеграл
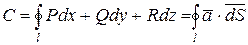 ,
,
где 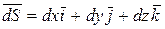 .
.
6. Формула Стокса устанавливает связь между циркуляцией векторного поля 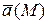 и его ротором:
и его ротором:
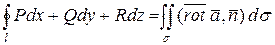 ,
,
где 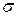 – поверхность, ограниченная замкнутым контуром
– поверхность, ограниченная замкнутым контуром 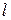 ,
, 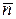 – единичный вектор нормали к этой поверхности. Направление нормали должно быть согласно с направлением обхода контура
– единичный вектор нормали к этой поверхности. Направление нормали должно быть согласно с направлением обхода контура 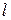 .
.
Пример 1.Найти наибольшее и наименьшее значения функции 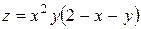 в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми 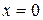 ,
, 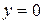 ,
, 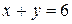 .
.
 Решение. Найдем стационарные точки, лежащие внутри данного треугольника:
Решение. Найдем стационарные точки, лежащие внутри данного треугольника:
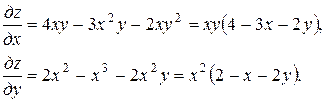
Приравнивая частные производные нулю, можно на 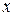 и
и 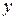 сократить, так как внутри треугольника
сократить, так как внутри треугольника 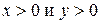 , тогда
, тогда
 .
.
Решение этой системы: 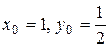 . Стационарная точка
. Стационарная точка 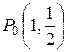 лежит внутри треугольника,
лежит внутри треугольника, 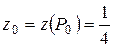 . На сторонах треугольника
. На сторонах треугольника 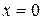 и
и 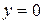 значение функции z равно нулю. Найдем наибольшее и наименьшее значения на стороне
значение функции z равно нулю. Найдем наибольшее и наименьшее значения на стороне 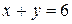 . На ней
. На ней 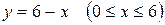 и
и
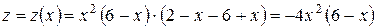 .
.
Стационарные точки находим из уравнения 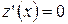 .
.
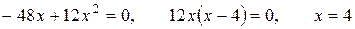 .
.
(т.к. х = 0 – граничная точка).
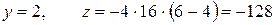 .
.
На концах интервала 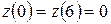 .
.
Таким образом, наибольшее и наименьшее значения функции z в данном треугольнике надо искать среди следующих ее значений:
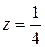 в точке
в точке 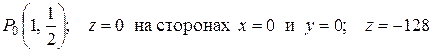 на стороне
на стороне 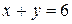 в точке (4, 2).
в точке (4, 2).
Сравнивая полученные значения видно, что наибольшее значение 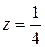 функция принимает внутри треугольника в точке
функция принимает внутри треугольника в точке 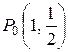 ; наименьшее значение z = - 128 – границе, в точке (4, 2).
; наименьшее значение z = - 128 – границе, в точке (4, 2).
Пример 2.Найти величину и направление наибольшего изменения функции 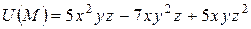 в точке
в точке 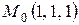 .
.
Решение. Находим частные производные функции U(M) в любой точке M(x, y, z) и в точке M0:
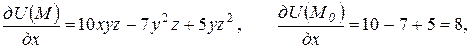
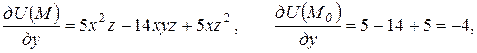
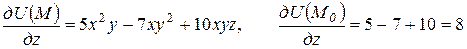 .
.
Тогда в точке 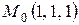 имеем
имеем 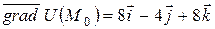 . Наибольшая скорость изменения поля в точке M0 достигается в направлении
. Наибольшая скорость изменения поля в точке M0 достигается в направлении 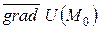
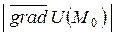 :
:
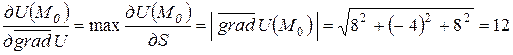 .
.
Пример 3.Вычислим работу силы 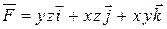 вдоль отрезка прямой АВ, если А(1, 1, 1) и В(2, 3, 4).
вдоль отрезка прямой АВ, если А(1, 1, 1) и В(2, 3, 4).
Решение. Запишем параметрические уравнения прямой АВ:
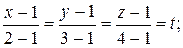
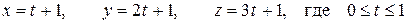 .
.
Тогда работа А силы 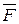 на пути АВ вычисляется по формуле
на пути АВ вычисляется по формуле
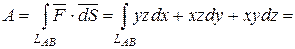
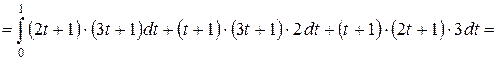
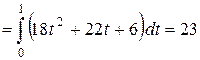 .
.
Пример 4. Вычислить циркуляцию векторного поля
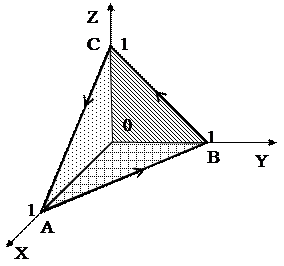
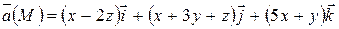 по контуру треугольника, полученного в результате пересечения плоскости
по контуру треугольника, полученного в результате пересечения плоскости 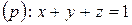 с координатными плоскостями при положительном направлении обхода относительно нормального вектора
с координатными плоскостями при положительном направлении обхода относительно нормального вектора 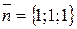 этой плоскости двумя способами: 1) используя определение циркуляции; 2) с помощью формулы Стокса.
этой плоскости двумя способами: 1) используя определение циркуляции; 2) с помощью формулы Стокса.
Решение. В результате пересечения плоскости (р) с координатными плоскостями получим треугольник АВС и укажем на нем положительное направление обхода контура АВСА.
1. Вычислим циркуляцию С данного поля по формуле:
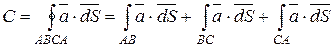 .
.
На отрезке АВ имеем:
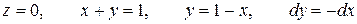 .
.
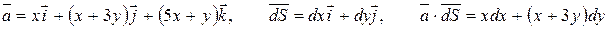 ,
,
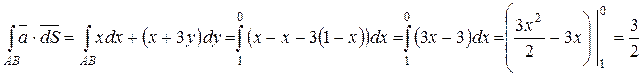 На отрезке ВС:
На отрезке ВС: 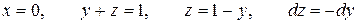 ,
,
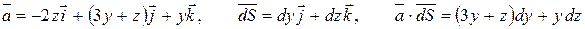 ,
,
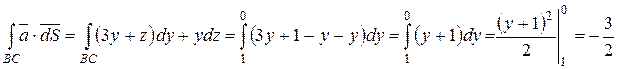
На отрезке СА: 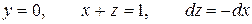 ,
,
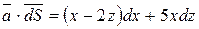 ,
,
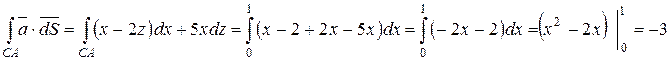 Следовательно,
Следовательно, 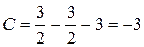 .
.
2. Вычислим циркуляцию данного поля с помощью формулы Стокса.
Для этого вычислим:
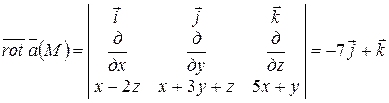 .
.
В качестве поверхности S в формуле Стокса возьмем боковую поверхность пирамиды ОАВС:
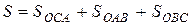 .
.
По формуле Стокса имеем:
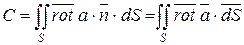 ,
,
где 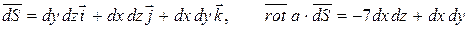 .
.
Следовательно,
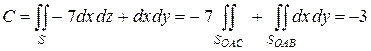 .
.
Дата добавления: 2016-02-16; просмотров: 2997;
