Задания для самостоятельной работы студента
1. Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.
2. Разобрать задачу-эталон.
3. Ответить на контрольные вопросы и тестовые задания в данном учебном пособии.
4. Решить ситуационные задачи.
Блок информации
| 1.Определение вариационного ряда | Вариационный ряд – это числовые значения признака, представленные в ранговом порядке с соответствующими этим значениям частотами. |
| 2.Основные обозначения вариационного ряда: | V – варианта, отдельное числовое выражение изучаемого признака; p - частота («вес») варианты, число ее повторений в вариационном ряду; n – общее число наблюдений (т.е. сумма всех частот, n=åp); Vmax и Vmin – крайние варианты, ограничивающие вариационный ряд (лимиты ряда); А – амплитуда ряда (т.е. разность между максимальной и минимальной вариантами, А= Vmax – Vmin). |
| 3. Виды вариационных рядов: | а) простой – это ряд, в котором каждая варианта встречается по одному разу (р=1); б) взвешенный – ряд, в котором отдельные варианты встречаются неоднократно (с разной частотой). |
| 4. Назначение вариационного ряда | Вариационный ряд необходим для определения средней величины (М) и критериев разнообразия признака, подлежащего изучению (s, СV). |
| 5. Средняя величина | Средняя величина - это обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность. |
| 6. Применение средних величин: | а) для оценки состояния здоровья – например, параметров физического развития (средний рост, средняя масса тела, среднее значение жизненной емкости легких и др.), соматических показателей (средний уровень сахара в крови, средняя величина пульса, средняя СОЭ и др.); б) для оценки организации работы лечебно-профилактических и санитарно-противоэпидемических учреждений, а также деятельности отдельных врачей и других медицинских работников (средняя длительность пребывания больного на койке, среднее число посещений на 1 час приема в поликлинике и др.); в) для оценки состояния окружающей среды. |
| 7. Методика расчета простой средней арифметической: | 1. Суммировать варианты: V1+V2+V3+…+Vn= åV; 2. Сумму вариант разделить на общее число наблюдений: M = åV/n. |
| 8. Методика расчета взвешенной средней арифметической (табл. 4.3.1) | 1. Получить произведение каждой варианты на ее частоту - Vp; 3. Найти сумму произведений вариант на частоты: V1p1 + V2p2 + V3p3 +...+ Vnpn = åVp; 3. Полученную сумму разделить на общее число наблюдений:M = åVp/n. |
| 9. Методика расчета среднеквадратического отклонения (см. табл. 4.3.1) | 1. Найти отклонение (разность) каждой варианты от среднеарифметической величины ряда (d = V – M);
2. Возвести каждое из этих отклонений в квадрат (d2);
3. Получить произведение квадрата каждого отклонения на частоту (d2p);
4.Найти сумму этих отклонений: d12p1+d22p2+d32p3+…+ dn2pn = åd2p;
5. Полученную сумму разделить на общее число наблюдений (при n<30 в знаменателе n-1):
åd2p/n;
6. Извлечь квадратный корень: 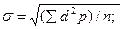 при n<30 при n<30 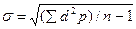
|
| 10.Применение среднеквадратического отклонения: | а) для суждения о колеблемости вариационных рядов и сравнительной оценки типичности (представительности) средних арифметических величин. Это необходимо в дифференциальной диагностике при определении устойчивости признаков; б) для реконструкции вариационного ряда, т.е. восстановления его частотной характеристики на основе правила «трех сигм». В интервале М±3s находится 99,7 % всех вариант ряда, в интервале М±2s – 95,5 % и в интервале М±1s – 68,3 % вариант ряда; в) для выявления “выскакивающих” вариант (при сопоставлении реального и реконструированного вариационных рядов); г) для определения параметров нормы и патологии с помощью сигмальных оценок; д) для расчета коэффициента вариации; е) для расчета средней ошибки средней арифметической величины. |
| 14. Коэффициент вариации (CV) | Коэффициент вариации - это процентное отношение среднеквадратического отклонения к среднеарифметической величине:
 CV = CV = 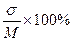 Коэффициент вариации – это относительная мера колеблемости вариационного ряда.
Коэффициент вариации – это относительная мера колеблемости вариационного ряда.
|
| 15. Применение коэффициента вариации | а) для оценки разнообразия каждого конкретного вариационного ряда и, соответственно, суждения о типичности отдельной средней (т.е. ее способности быть полноценной обобщающей характеристикой данного ряда). При СV <10 % разнообразие ряда считается слабым, при СV от 10 % до 20 % – средним, а при СV >20 % – сильным. Сильное разнообразие ряда свидетельствует о малой представительности (типичности) соответствующей средней величины и, следовательно, о нецелесообразности ее использования в практических целях.
б) для сравнительной оценки разнообразия (колеблемости) разноименных вариационных рядов и выявления более и менее стабильных признаков, что имеет значение в дифференциальной диагностике. 
|
Задача-эталон
Условие задачи. В городе N в 2007 году проведено измерение массы тела 7-летних мальчиков (данные представлены в табл. 4.3.1). По данным аналогичного исследования, выполненного в городе N в 1997 году, средняя масса тела 7-летних мальчиков составила 23,8 кг, s ± 3,6 кг.
Задание. 1. Вычислить среднюю арифметическую величину (М) и критерии разнообразия вариационного ряда (s,СV).
2. Оценить полученные результаты, сравнить их с данными предыдущего исследования, сделать соответствующие выводы.
Таблица 4.3.1.
Результаты измерения массы тела 7-летних мальчиков города N в 2007 г.
| Масса тела (в кг) V | Середина интервала (центральная варианта) V1 | Число мальчиков p | Vp | d=(V-M) | d2 | d2p |
| 15-18,9 | -7 | |||||
| 19 – 22,9 | -3 | |||||
| 23 – 26,9 | +1 | |||||
| 27 – 30,9 | +5 | |||||
| 31 – 34,9 | +9 | |||||
| n = 100 | åVp=2400 | åd2p=2188 |
Решение задачи
В сгруппированном вариационном ряду центральная варианта рассчитывается как полусумма начальных вариант соседних интервалов;
М = åVp /n = 2400/100 = 24,0 (кг);

 s = Ö åd2p /n = Ö 2188/100 = ± 4,68 (кг);
s = Ö åd2p /n = Ö 2188/100 = ± 4,68 (кг);
CV = (s /М)х100 = (4,68/24,0 х 100)= 19,5 %.
Выводы:
1. Средняя масса тела 7-летних мальчиков в г.N в 2007 году составляет 24,0 кг,
2. s = ±4,68 (кг).
3. Величина коэффициента вариации, равная 19,5 % свидетельствует о среднем разнообразии признака (приближающемся к сильному).
Таким образом, можно считать, что полученная средняя величина массы тела является достаточно представительной (типичной). По сравнению с 1997 годом, в 2007 году отмечается более значительная вариабельность массы тела у мальчиков 7 лет (±4,68 кг против 3,6 кг). Аналогичный вывод вытекает и из сопоставления коэффициентов вариации (CV в 1997году равен (3,6 /23,8 х 100 = 15,1 %).
Контрольные вопросы
1. Что такое вариационный ряд?
2. Для чего используются средние величины?
3. По каким критериям можно оценить разнообразие признака?
4. В каких случаях применяют среднеквадратическое отклонение?
5. Каково назначение коэффициента вариации?
6. Как оценить величину коэффициента вариации?
Тестовые задания
Выберите один или несколько правильных ответов:
1. Вариационный ряд – это:
а) числовые значения изучаемого признака статистической совокупности, расположенные в ранговом порядке;
б) числовые значения изучаемого признака, расположенные в ранговом порядке с соответствующими этим значениям частотами;
в) числовые значения изучаемого признака с соответствующими этим значениям частотами.
2. Средняя величина – это:
а) варианта с повторяющимся числовым значением;
б) варианта, имеющая наибольший «вес» (частоту) в вариационном ряду;
в) обобщающая числовая характеристика размера изучаемого признака.
3. Впишите недостающий вид вариационного ряда по частоте представленных в нем вариант:
а) простой;
б) __________________.
4. Средние величины применяются для оценки:
а) состояния здоровья населения;
б) организации работы и деятельности лечебно-профилактических учреждений в целом, отдельных его подразделений и врачей;
в) организации работы и деятельности всей системы здравоохранения;
г) состояния окружающей среды.
5. В каком вариационном ряду используются следующие методы расчета средней арифметической величины (подберите соответствующие ответы):
| Вариационный ряд: 1. простой вариационный ряд; 2. взвешенный вариационный ряд. | Методы расчета: а) М = (åVр)/n; б) М = åV/n. |
6. Укажите соответствующий алгоритм расчета для простых и взвешенных средних арифметических величин:
| Средняя величина: 1. простая средняя арифметическая величина; 2. взвешенная средняя арифметическая величина. | Алгоритм расчета: а) перемножить каждую варианту на соответствующую ей частоту (Vр); б) получить сумму произведений вариант на частоты (åVр); в) суммировать числовые значения вариант (åV); г) полученную åVр разделить на число наблюдений (n); д) полученную åV разделить на число наблюдений (n). |
7. Характеристиками разнообразия вариационного ряда являются:
а) лимиты ряда (Vmax и Vmin);
б) амплитуда ряда (А);
в) среднеквадратическое отклонение (s);
г) отклонение (разность) каждой варианты от среднеарифметической величины вариационного ряда (d = V – M);
д) коэффициент вариации (СV).
8. Каково значение сигмы для анализа вариационного ряда (укажите правильные ответы):
а) характеризует внутреннее разнообразие (колеблемость) вариационного ряда;
б) применяется для сравнительной оценки типичности средних арифметических величин;
в) позволяет оценить достоверность средней величины;
г) позволяет восстановить (реконструировать) вариационный ряд по частоте на основе правила “трех сигм”;
д) применяется для выявления “выскакивающих” вариант;
е) применяется для расчета коэффициента вариации (СV);
ж) применяется для вычисления ошибки репрезентативности средней арифметической (mM).
9. «Нормальное» распределение вариационного ряда означает:
а) распределение вариационного ряда по частоте на основе правила «трех сигм»;
б) что в пределах М±1s находится 68,3 % вариант ряда;
в) что в пределах М±2s находятся 95,5 % всех вариант;
г) что в пределах М±3s находятся 99,7 % всех вариант.
Ситуационные задачи
Задача 1
Результаты исследования здоровья студентов 2-х групп по характеристике частоты сердечных сокращений (ЧСС) показали одинаковую среднюю величину (85 уд/мин). Критерий разнообразия ЧСС в одной группе - 2 уд ара в минуту, в другой – 4 удара в минуту.
1. Определите, для какой группы средняя величина пульса при одинаковой средней частоте сердечных сокращений (М) и одинаковом числе студентов типичнее, т.е. лучше отражает состояние здоровья студентов.
2. Какой критерий разнообразия был использован для определения разнообразия признака?
Задача 2
При изучении физического развития школьников 7-го класса было установлено значительное разнообразие по росту (от 151 см до 170 см). Средняя величина роста этих мальчиков равна 160 см, σ= ±3 см.
1. Находятся ли крайние значения роста детей в пределах нормального распределения признака?
2. Какую методику (значение сигмы) Вы при этом использовали?
Задача 3
При медицинском осмотре студентов военно-медицинской академии изучены различные показатели крови, в т.ч. количество лейкоцитов колебалось в пределах 6000 -9500. Среднее значение числа лейкоцитов равно 7500, σ= ±0,5 тыс. лейкоцитов.
1. Какая величина в данном случае является «выскакивающей вариантой»?
2. Какая методика позволила определить ее?
Задача 4
В первые часы после инфаркта миокарда у больных изменяется целый ряд параметров, в том числе уровень артериального давления, количество лейкоцитов и ферментов крови.
1. Какой критерий необходимо применить для оценки разнообразия признаков?
2. Обоснуйте его применение.
Задача 5
При проведении всеобщей диспансеризации детского населения в городе Н. были получены результаты изучения физического развития детей (по массе тела). При этом получили следующие данные: средняя масса тела новорожденных детей составила 2,9 кг, σ ± 0, 3 кг; средняя масса тела детей 1-го года жизни – 12 кг , σ ± 1,0 кг.
1. Достаточно ли представленной в условии задачи информации для вывода о степени разнообразия (устойчивости) признака?
2. В какой группе более разнообразна масса тела?
Список литературы
Основная:
1.Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. – М.:ГЭОТАР – МЕД, 2002.- 520 с.
2. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению. – Часть I. Общественное здоровье. – М.: Медицина. – 2003. – 364 с.
3. Социальная медицина и организация здравоохранения (Руководство в 2-х томах). Миняев В.А., Вишняков Н.И. и др. - СПб, 1998. - 528 с.
4. Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. – Москва, 2000. – 432 с.
Дополнительная:
1. С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. –459 с. – С. 27-36.
4.4. Метод стандартизации
Введение
При изучении общественного здоровья и здравоохранения в научных или практических целях исследователю нередко приходится доказывать влияние факторных признаков на результативные при сравнении двух или более совокупностей. С этой целью применяется целый ряд статистических приемов.
При сравнении двух неоднородных совокупностей по какому-либо признаку (составу) применяются методы стандартизации (прямой, обратный, косвенный).
В данном учебном пособии рассматривается прямой метод стандартизации. Этот метод применяется при наличии полных сведений как о составе сравниваемых совокупностей, так и о распределении в них явления.
Цель изучения темы
На основе применения метода стандартизации уметь выявлять влияние факторного признака на результативный при изучении общественного здоровья и анализе деятельности медицинских учреждений.
По окончании изучения темы студент должен:
Уметь:
· вычислять стандартизованные показатели;
· сопоставлять интенсивные и стандартизованные показатели и делать соответствующие выводы;
· применять метод стандартизации при решении конкретных задач, связанных с изучением общественного здоровья и деятельности учреждений здравоохранения.
Знать:
· условия применения метода стандартизации;
· сущность и назначение метода;
· этапы расчета стандартизованных показателей.
Дата добавления: 2016-02-16; просмотров: 4330;
