Методы моделирования и экспериментального исследования радиоприемных устройств
Математическое моделирование радиоустройств (РУ) на ЭВМ является прогрессивным и весьма экономичным способом их исследования на ранних этапах проектирования, когда РУ, в частности РПУ, еще не создано «в металле» и натурные испытания не возможны.
Математическое моделирование — это исследование объекта с помощью математической модели, которая математическими формулами и соотношениями описывает наиболее важные черты оригинала.
Математическое моделирование называется машинным, если математическая модель реализована на ЦВМ (в виде цифровой модели), АВМ (в виде аналоговой модели) или АЦВМ (в виде гибридной аналого-цифровой модели). Математическое моделирование часто используется как составная часть полунатурного моделирования.
Задачи математического моделирования вытекают из задач, поставленных перед исследователем. Применительно к РПУ, можно выделить следующие задачи:
1) статистический синтез и анализ оптимальных РПУ в рамках пространственно-временной и временной фильтрации;
2) статистический анализ помехозащищенности оптимальных, квазиоптимальных и эвристических структурных схем РПУ;
3) проектирование РПУ в целом (в том числе автоматизированное) или их отдельных узлов.
Классификация методов математического моделирования.
Методы составления математических моделей РПУ и их звеньев довольно разнообразны и различаются по нескольким классификационным признакам.
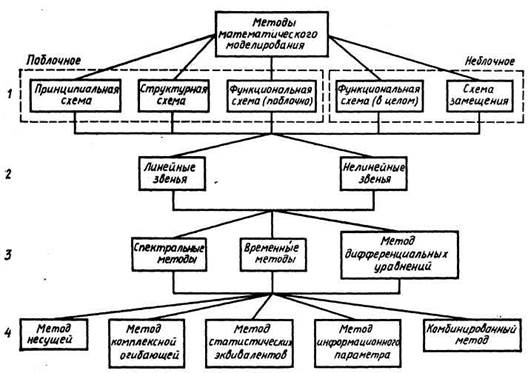
По типу схемы, на основе которой составляется математическая модель (уровень 1), различают: принципиальную, структурную, функциональную схемы и схему замещения. При поблочном моделировании применяют первые три схемы, при неблочном — последние две.
По типу моделируемого звена РПУ (уровень 2) различают линейные и нелинейные звенья. Последние подразделяются на безынерционные и инерционные (функциональные, нефункциональные). Функциональные инерционные нелинейные звенья могут быть представлены последовательным соединением безынерционного и инерционного нелинейных звеньев. В нефункциональных инерционных нелинейных звеньях такое разделение невозможно.
По методу математического описания преобразований сигналов в моделируемых звеньях РПУ (уровень 3) различают: спектральные методы (преобразования Лапласа и Фурье), временные методы (интеграл Дюамеля, ортогональные разложения) и метод дифференциальных уравнений.
По методу описания входных воздействий (уровень 4) различают пять функциональных методов: несущей, комплексной огибающей, статистических эквивалентов, информационного параметра, комбинированный.
Так, в качестве входных воздействий в модели могут фигурировать:
низкочастотный сигнал s(t) или модулированный сигнал (радиосигнал) uc[t, lc(t)];
комплексная огибающая 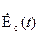 модулированного сигнала;
модулированного сигнала;
информационный параметр lc(t), заложенный в модулированный сигнал.
В методе несущей в качестве входного воздействия выбирают сигнал s (t) или радиосигнал uc[t, lc(t)].
В методе комплексной огибающей все сигналы и помехи постулируют в виде узкополосных сигналов и в качестве входных воздействий в модели берут их комплексную огибающую.
В методе статистических эквивалентов моделируемое радиозвено с входным радиосигналом uc[t, l(t)] и выходным эффектом z[t, l(t)] заменяют статистическим эквивалентом с входным воздействием l(t) и выходным сигналом zэ[t, l(t)], статистически адекватным (по математическому ожиданию, дисперсии и т. п.) реальному сигналу z[t, l(t)].
Метод информационного параметра применяют для моделирования следящих радиоустройств, выделяющих на выходе оценку 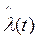 информационного параметра l(t), заложенного во входной радиосигнал uc[t, l(t)]. Суть метода сводится к замене следящего РУ с входным радиосигналом uc[t, l(t)] цепью автоматического регулирования с входным воздействием l(t) и тем же выходом
информационного параметра l(t), заложенного во входной радиосигнал uc[t, l(t)]. Суть метода сводится к замене следящего РУ с входным радиосигналом uc[t, l(t)] цепью автоматического регулирования с входным воздействием l(t) и тем же выходом 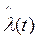 .
.
При комбинированном методе в качестве входного воздействия берут комплексную огибающую, но при моделировании используют и метод несущей.
Математическое описание сигналов и помех.
Для математического описания детерминированных колебаний s(t) или u(t) применяют спектральные и временные методы, а также метод дифференциальных уравнений.
Для математического описания случайных колебаний (квазидетерми-нированных радиосигналов, случайных сигналов и помех) применяют теорию вероятностей, широко используемую в статистической радиотехнике.
Математическое описание звеньев РПУ.
Для этого применяют основные соотношения из теории цепей. Так, стационарные линейные динамические звенья (ЛДЗ) описываются с помощью импульсной характеристики (ИХ) h (t), переходной характеристики (ПХ) g(t), передаточной функции (ПФ) К (р) и комплексной частотной характеристики (КЧХ) К(jω).
В рамках временного метода (интеграл Дюамеля) пользуются интегралом свертки, который связывает произвольные входное х (t) и выходное у (t) колебания ЛДЗ с помощью интеграла
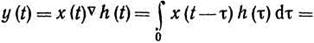
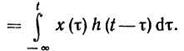
В спектральном методе Лапласа прибегают к изображениям входного X(р) и выходного Y(р) сигналов:

В спектральном методе Фурье применяют понятия комплексных спектров X(jω), Y(jω)входного и выходного сигналов соответственно:
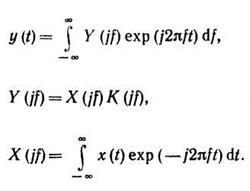
Нестационарные ЛДЗ описываются чаще всего временными методами с помощью двух типов импульсных характеристик:
а) ω(t, ξ)— реакция ЛДЗ в момент времени t на единичный импульс δ(t-t0), поданный в момент времени t0==ξ;
б) h(t, τ) — реакция ЛДЗ в момент времени t на единичный импульс, поданный на τс ранее. В этом случае имеем
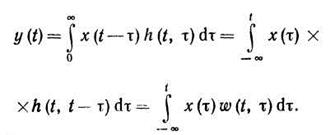
На основе вышеприведённых соотношений описываются все линейные звенья РПУ (входная цепь, УРЧ, УПЧ, УНЧ и т. д.) в рамках метода несущей. В рамках метода комплексной огибающей эти соотношения преобразуют для комплексных огибающих.
Безынерционные нелинейные звенья (БНЗ) с заданной «вольт-амперной характеристикой» у = G(х) описываются либо временным методом
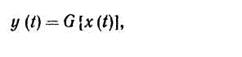
либо спектральным методом
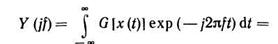
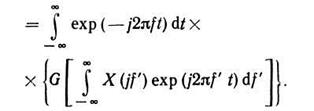
Безынерционные нелинейные радиозвенья (БНРЗ), состоящие из последовательного соединения БНЗ и узкополосного ЛДЗ, настроенного на n-ю гармонику (п = 0, 1, ...) входного узкополосного сигнала, описываются специальными методами (метод огибающей и фазы, метод контурных интегралов и др.), распространенными в статистической радиотехнике. Эти методы чаще всего применяются в рамках метода комплексной огибающей.
Типовые звенья РПУ, состоящие из последовательно включенных ЛДЗ (например, УПЧ), БНЗ (например, детектора или ограничителя) и ЛДЗ (например, УНЧ или УПЧ), анализируются чаще всего временными методами поблочно.
Следящие звенья РПУ обычно описываются в рамках временных методов либо системой интегро-дифференциальных уравнений, либо дифференциальным уравнением высокого порядка.
Методы составления цифровых моделей (методы оцифровывания математических моделей)
Общие методы оцифровывания.Методы оцифровывания аналоговых математических моделей сводятся к следующим операциям:
- замене аналоговых сигналов х (t), у (t) их решетчатыми функциями х [п], у [п], с шагом дискретизации Т;
- введению в цепи обратной связи следящих РТУ задержки на один шаг дискретизации z-1 так что вместе у [п] имеем у [п — 1];
- применению различных способов представления линейных инерционных звеньев в виде цифровых фильтров (способы скользящего суммирования, рекуррентных разностных уравнений и др.);
- замене дифференциальных уравнений разностными уравнениями с использованием интерполяционных методов Эйлера, Рунге — Кутта и др.
Методы составления цифровых моделей линейных динамических звеньев.
При цифровом моделировании ЛДЗ стремятся обеспечить максимальное совпадение выходных дискретных значений ЦФ уЦ[п] = у [п] и дискретных выборок у.А ×(пТ) = у (пТ) моделируемого аналогового фильтра. Существует ряд методов обеспечения равенства у [п] = у (пТ) с применением теории нерекурсивных и рекурсивных ЦФ.
Цифровые модели ЛДЗ на нерекурсивных ЦФ. Метод скользящего суммирования применяется при описании ЛДЗ интегралом Дюамеля и состоит в замене интегрирования суммированием:
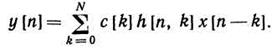
Здесь коэффициенты с [k] зависят от способа аппроксимации.
Метод инвариантности импульсной характеристики предусматривает (например, для стационарного ЛДЗ) выбор импульсной характеристики ЦФ h [k] в соответствии с равенством h [k] = Th (kT), где h (t) — импульсная характеристика моделируемого фильтра. Это соответствует цифровому алгоритму модели ЛДЗ:
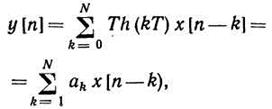
где ak = h [k] = Th (kT) — коэффициенты.
Этим алгоритмам соответствует цифровая модель нерекурсивного ЦФ (рис. а)
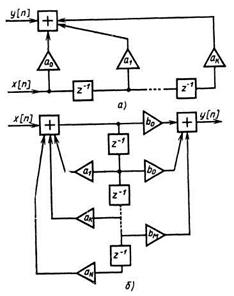
с передаточной функцией
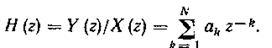
Цифровые модели ЛДЗ на рекурсивных ЦФ. Метод рекуррентных разностных уравнений предусматривает замену передаточной функции моделируемого фильтра
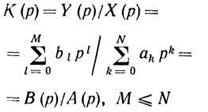
ее цифровым аналогом
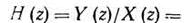
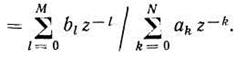
Это эквивалентно (при а0 = 1) заданию рекуррентного разностного уравнения цифровой модели ЛДЗ:
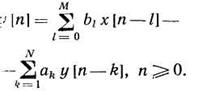
|
Метод билинейного z-преобразования предусматривает задание ПФ Н(z) путем подстановки
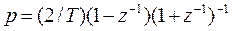
В передаточную функцию К (р) моделируемого ЛДЗ. Так, например, для инерционного ЛДЗ первого порядка К(p)=(1+pτ)-1 после подстановки p, из выражения выше, имеем Н(z) = (b0+b1z-1)(1+a1z-1), где b0 = b1 = T/(T+2τ), a1 = (T-2τ)/( T+2τ).
Метод согласованного z-преобразования используется, когда ПФ моделируемого ЛДЗ задана в виде
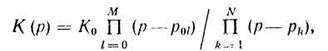
где p0l — нули; pk —- полюсы.
В этом случае Н (z) цифрового фильтра находят путем замены каждого сомножителя в числителе и знаменателе по формуле
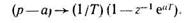
|
Если в ПФ моделируемого звена все полюсы простые, то, вычислив вычеты Am-= К(р) (р — pm)|P-Pm можно найти импульсную характеристику аналогового моделируемого ЛДЗ:
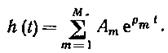
Подстановка этого выражения в выражение цифрового алгоритма ЛДЗ позволяет использовать цифровую модель нерекурсивного ЦФ с коэффициентами
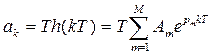
Наоборот, от модели на нерекурсивном ЦФ можно перейти к модели на рекурсивном ЦФ. Для этого надо подставить выражение для описания звена в выражение для алгоритма модели ЛДЗ и записать
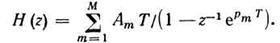
Приводя это выражение к форме, соответствующей цифровому аналогу модели, мы придем к цифровой модели рекурсивного ЦФ.
Цифровые модели комплексных ЛДЗ. В рамках метода комплексной огибающей приходится составлять цифровые модели комплексных линейных фильтров, имеющих обычно нереализуемую в аналоговом виде импульсную характеристику 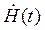 , связывающую комплексные огибающие на входе и выходе интегралом
, связывающую комплексные огибающие на входе и выходе интегралом
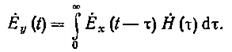
Тогда методом скользящего суммирования нетрудно получить соответствующую цифровую модель комплексного ЦФ:
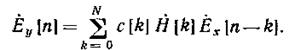
Часто комплексные огибающие разбивают на действительную и мнимую части:
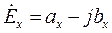

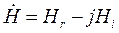
Тогда приходим к уравнениям
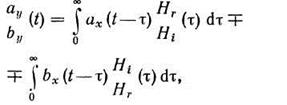
|
соответствующим модели ЦФ, соответствующей структуре
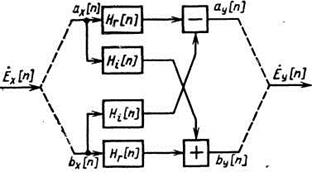
и описываемо соотношениями
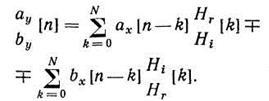
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Анализ шумовых характеристик цепей | | | Одноконтурные перестраиваемые входные цепи. |
Дата добавления: 2016-04-14; просмотров: 2102;
