Метод кусочно-линейной аппроксимации

Лекция N 40

В соответствии с определением данного метода, расчет нелинейной цепи с его использованием включает в себя в общем случае следующие основные этапы:

1. Исходная характеристика нелинейного элемента заменяется ломаной линией с конечным числом прямолинейных отрезков.

2. Для каждого участка ломаной определяются эквивалентные линейные параметры нелинейного элемента и рисуются соответствующие линейные схемы замещения исходной цепи.

3. Решается линейная задача для каждого отрезка в отдельности.

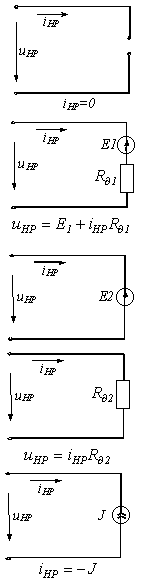
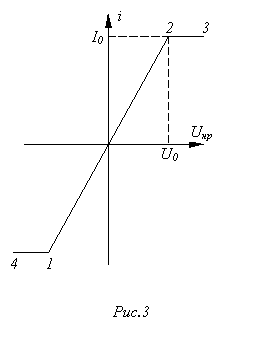
Пусть вольт-амперная харак-теристика (ВАХ) нелинейного резистора имеет форму, представленную на рис. 1. Заменяя ее ломаной линией 4-3-0-1-2-5, получаем приведенные в табл. 1 расчетные эквивалентные схемы замещения и соответ-ствующие им линейные соотношения.

Расчет каждой из полученных линейных схем замещения при наличии в цепи одного нелинейного элемента и произвольного числа

линейных не представляет труда. В этом случае на основании теоремы об активном двухполюснике исходная нелинейная цепь сначала сводится к схеме, содержащей эквивалентный генератор с некоторым линейным внутренним сопротивлением и последовательно с ним включенный нелинейный элемент, после чего производится ее расчет. При наличии в цепи переменного источника энергии рабочая (изображающая) точка будет постоянно скользить по аппроксимирующей характеристике, переходя через точки излома. Переход через такие точки соответствует мгновенному изменению схемы замещения. Поэтому задача определения искомой переменной сводится не только к расчету схем замещения, но и к определению моментов “переключения” между ними, т.е. нахождению граничных условий по времени. Анализ существенно усложняется, если в цепи имеется несколько нелинейных элементов. Главная трудность в этом случае связана с тем, что заранее не известно сочетание линейных участков, соответствующее заданному входному напряжению (току). Искомое сочетание линейных участков всех нелинейных элементов определяется перебором их возможных сочетаний. Для любого принятого сочетания параметры схемы известны, и, следовательно, могут быть определены напряжения и токи для всех элементов. Если они лежат в пределах соответствующих линейных участков, то принятое сочетание дает верный результат. Если хотя бы у одного нелинейного элемента переменные выходят за границы рассматриваемого линейного участка, то следует перейти

Таблица 1. Кусочно-линейная аппроксимация ВАХ нелинейного резистора

Участок аппроксимирующей кривой	Схема замещения	Параметры элементов	Граничные условия
0 - 1 1 - 2 2 - 5 3 - 0 2 - 5

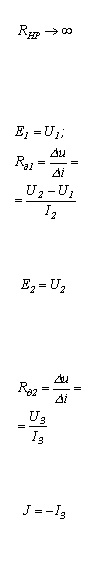
к другому сочетанию. Необходимо отметить, что всегда имеется единственное сочетание линейных участков характеристик нелинейных элементов, соответствующее изменению входного сигнала в некоторых пределах.

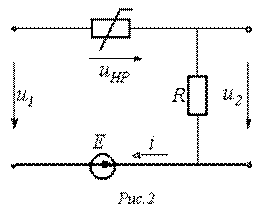
В качестве примера определим напряжение 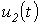в цепи на рис. 2, в которой 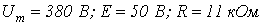. ВАХ нелинейного резистора приведена на рис. 3, где .

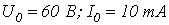Решение

1. В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением

,

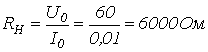на участке 2-3-источником тока с током 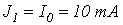и на участке 4-1-источником тока с током .

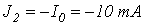2. На основании данной эквивалентной замены для тока на участке 1-2 ВАХ можно записать:

(1)

откуда

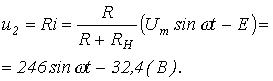
При движении изображающей точки по участку 2-3 ВАХ имеем

,

при движении по участку 1-4 ВАХ-

.

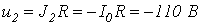3. Определяем интервалы движения изображающей точки по отдельным участкам ВАХ. Для точки излома 1 на основании (1) справедливо уравнение

или

.

Отсюда получаем два значения мгновенной фазы питающего напряжения на одном периоде, соответствующих точке 1: 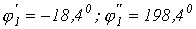. Первое значение определяет переход изображающей точки с участка 4-1 на участок 1-2, второе – с участка 2-1 на участок 1-4.

Аналогично записываем для точки 2 излома ВАХ

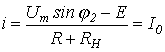
или

откуда 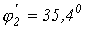(значение, соответствующее переходу с участка 1-2 на участок 2-3) и 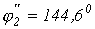(значение, соответствующее переходу с участка 3-2 на участок 2-1).

Таким образом, получаем для одного периода питающего напряжения

;

;

;

;

.

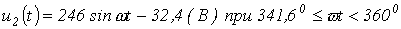
В соответствии с периодичностью синусоидальной функции данные решения повторяются через 360°n.

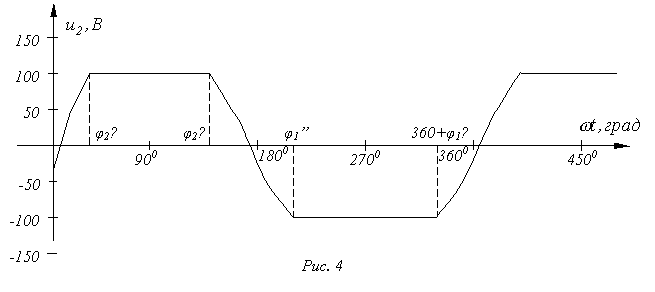
На рис. 4 представлен график зависимости искомой величины.