Главные направления и главные диаметры

Определение. Неасимптотическое направление линии второго порядка называется главным, если оно перпендикулярно диаметру, сопряжённому с хордами, имеющими это направление. Этот диаметр называется главным диаметром линии второго порядка. Он является осью симметрии линии.

Теорема 1. Координаты 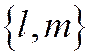вектора (ненулевого), имеющего главное направление относительно линии второго порядка, заданной общим уравнением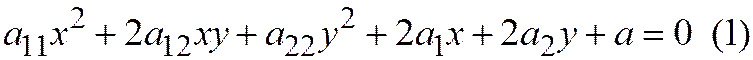

относительно ДПСК определяется из системы:

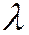где - отличный от нуля корень квадратного уравнения .

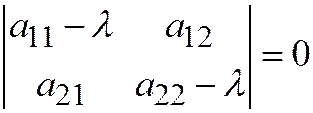Или 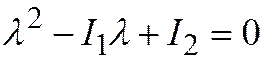, где , .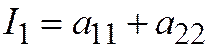

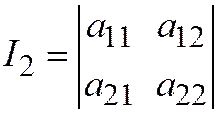Доказательство. Пусть ненулевой вектор 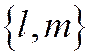не имеет асимптотического направления линии (1). Тогда уравнение диаметра, сопряжённого с хордами линии (1) параллельными вектору 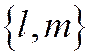. Имеет вид: 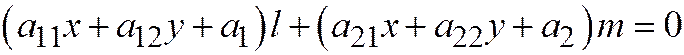, или

.

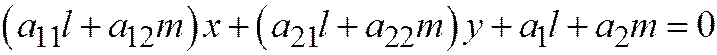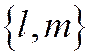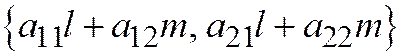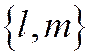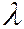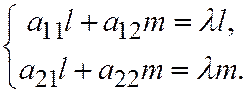Так как система координат прямоугольная, то этот диаметр перпендикулярен хордам, параллельным ненулевому вектору тогда и только тогда, когда ненулевые векторы и коллинеарны, т.е. тогда и только тогда, когда существует такое число , что (2)

В этих соотношениях 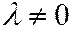, т.к. в противном случае мы имели бы 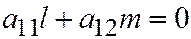; 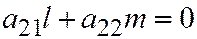, откуда: 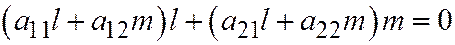, или 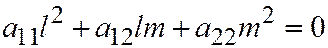, т.е. вектор 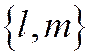имел бы асимптотическое направление.

Далее, переписывая систему (2) в виде

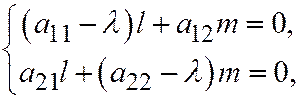и замечая, что она имеет ненулевое решение 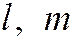, заключаем, что 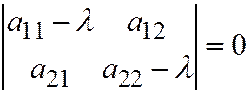. (3) Обратно, уравнение (3) всегда имеет действительные корн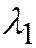и и 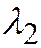. В самом деле, переписывая его в виде: 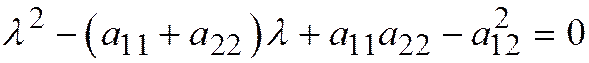, находим дискриминант :

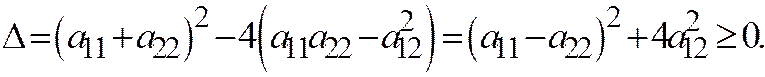Случай 1. 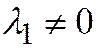, 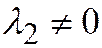и 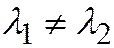(эллипс действительный или мнимый, гипербола, две пересекающиеся прямые, действительные или мнимые).

В этом случае система (2) при 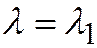принимает вид: 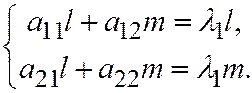(4). И, в силу условия:

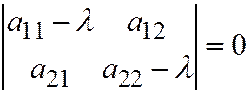имеет ненулевое решение 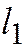, 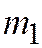. Из соотношения (4) для этого решения, которые принимают вид: 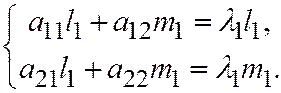(5). Находим (первое уравнение умножим на 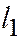, второе на 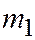и сложим):

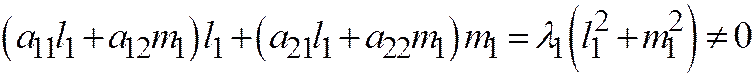или .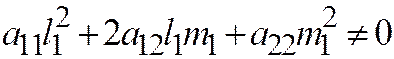

Значит, это решение не имеет асимптотического направления линии (1), а в силу соотношений (4) ненулевой вектор 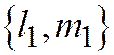имеет главное направление линии (1).

Аналогично при 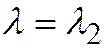из системы (2) находим ненулевой вектор 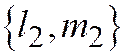, такой что 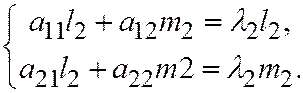(6). Также имеющий главное направление относительно линии (1).

Докажем, что векторы 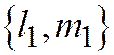и 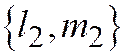перпендикулярны. Из соотношений (5) и (6) находим (в системе (5) первое уравнение умножим на 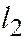, второе на 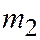, а в системе (6) на 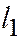и ):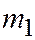

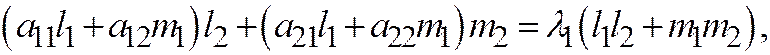
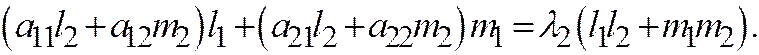Левые части этих равенств одинаковые, значит: 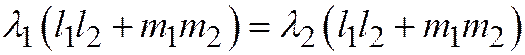, или

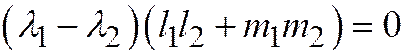, откуда, т.к. 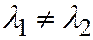: 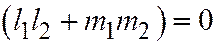. т.е. векторы 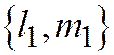и 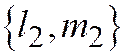взаимно перпендикулярны.

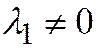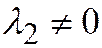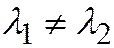Отсюда также следует, что в случае , и система (2) при 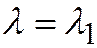имеет ненулевое решение, но не может иметь двух линейно независимых решений (то же и при 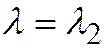). Иначе говоря, линия имеет два и только два взаимно перпендикулярных и главных диаметра.

Случай 2. 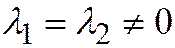(окружность действительная, нулевая или мнимая). В этом случае асимптотических направлений нет и любое направление является главным; уравнение диаметра:

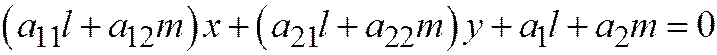, сопряжённого хордам, параллельным ненулевому вектору 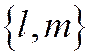принимает вид:

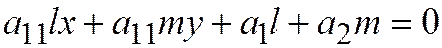и является уравнением прямой, перпендикулярной вектору , .

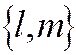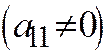Главным диаметром в этом случае является любая прямая 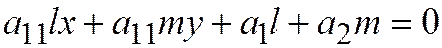, проходящая через центр линии.

Случай 3. , 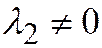(парабола, две параллельные или совпадающие прямые).

В этом случае 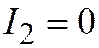. Система (2) при 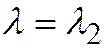имеет ненулевое решение 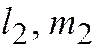; вектор 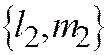не имеет асимптотического направления линии (1) и имеет главное направление.

При 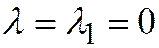система (2) принимает вид:

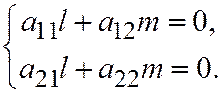Эта система имеет ненулевое решение 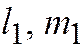, однако вектор 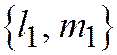имеет асимптотическое направление, т.к. из соотношений 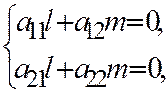следует, что .

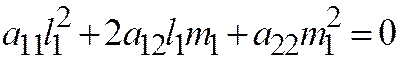Векторы 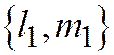, 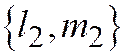и здесь ортогональны (в силу того, что 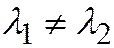, доказательство дано выше).

Отсюда следует, что система 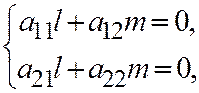в этом случае имеет одно ненулевое решение, но не имеет двух линейно независимых решений.