Метод сортировки по глубине

Удаление невидимых линий и граней

Общие замечания

Удаление невидимых линий производится до проецирования объекта.

Алгоритмы удаления невидимых граней могут быть условно поделены на два класса в зависимости от принципов, заложенных для их реализации. Первый класс – это алгоритмы, работающие в пространстве объекта. Это означает, что для определения видимости данной грани сравнивается ее взаимное расположение со всеми остальными гранями в трехмерной сцене. Пусть N – количество граней в трехмерной сцене. Для построения трехмерной сцены в этом случае необходимо сравнить положение каждой грани с оставшимися, что требует порядка N² операций. Например, пусть количество граней в трехмерной сцене N = 1000, тогда время работы алгоритмов этого класса порядка 1,000,000 операций.

Другой класс алгоритмов – алгоритмы, работающие в пространстве изображения, основан на нахождении точки ближайшей грани, которую пересекает луч зрения, проходящий через заданную точку на растре. Поскольку число точек на растровом экране фиксировано, то алгоритмы этого класса менее чувствительны к увеличению количества объектов в трехмерной сцене. Пусть n - число точек на растровом экране. Тогда количество операций, необходимых для построения трехмерной сцены будет порядка n´N. Например, для экранного разрешения 320´200 точек, n = 64000, тогда количество операций для N = 1000 граней будет порядка 64,000,000. Выбор класса алгоритма может зависеть от особенностей конкретной задачи, а также от способов реализации алгоритма.

Определение видимости или не видимости точки по сути сводится к проверке, лежат ли две точки на одном проекторе (см. рисунок …).

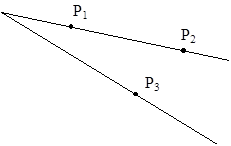
Рисунок … Проверка взаимной видимости точек

Если проекция параллельная, то проверка сводится к сравнению координат

x₁ = x₂, y₁ = y₂;

Если проекция центральная, то проверки становятся значительно сложнее:

, .

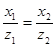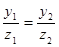Те же самые вычисления придется повторить для новой точки P₃.

Для эффективного решения задачи удаления невидимых ребер/граней преобразуем видимый объем, как показано на рис. 33.

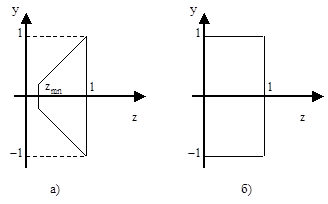
Рис. 33. Изменение видимого объема при перспективном преобразовании: а) до преобразования; б) после преобразования.

Это достигается с помощью матрицы

,

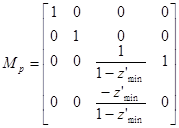которая носит название перспективного преобразования. После применения матрицы M_p нормированный видимый объем становится прямоугольным параллелепипедом, что позволяет перейти от центральной перспективной к параллельной проекции. Легко проверить, что, например,

.

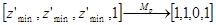При выполнении различных операций по выявлению перекрывающих друг друга граней широко используют ограничивающие грань тела (оболочки). В качестве оболочек чаще всего используют параллелепипеды с гранями, параллельными координатным плоскостям. Если такой ограничивающий грань параллелепипед задан координатами своих диагональных углов (x_min, y_min, z_min) и (x_max, y_max, z_max), то проверка пересечения оболочек двух граней сводится к простой процедуре проверки пересечения трех промежутков: от x_min до x_max, от y_min до y_max и от z_min до z_max. Если хотя бы один из этих промежутков не пересекается с аналогичным промежутком для оболочки другой грани, то оболочки граней не пересекаются и, следовательно, грани тоже не пересекаются. Грани, оболочки которых пересекаются, могут как пересекаться, так и не пересекаться, и в этом случае проводят более сложные вычисления.

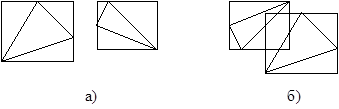
Рисунок. … Многоугольники и их оболочки: а) оболочки не пересекаются, следовательно многоугольники не пересекаются; б) оболочки пересекаются, а многоугольники нет.

Метод Z – буфера

Рассмотрим алгоритм удаления невидимых граней с использованием z-буфера. Этот алгоритм часто используется в современных приложениях компьютерной графики. Он работает в пространстве изображения и применяется в таких популярных графических библиотеках как OpenGL и Direct3D.

Алгоритм работает в параллельной проекции. Пусть размеры окна вывода или экрана составляют X точек в ширину и Y точек в высоту. В качестве z-буфера заведем двумерный прямоугольный массив чисел по размерности совпадающий с окном вывода или экрана, т.е. X 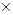Y. В z-буфере будут храниться текущие значения z-координат каждого пиксела.

В начале работы алгоритма в z-буфер заносятся значения, соответствующие бесконечности. Каждая грань трехмерного объекта, представленная в виде многоугольника, преобразуется в растровую форму. При разложении в растр для каждой точки многоугольника вычисляется значение ее z-координаты. Если z-координата оказалась меньше чем текущее значение в z-буфере, то в z-буфер заносится z-координата точки, и на экране рисуется точка цветом текущего многоугольника. После разложения в растр всех многоугольников изображение трехмерной сцены построено.

Рассмотрим способ ускоренного вычисления z-координат при разложении многоугольников в растр. Запишем уравнение плоскости, образуемой многоугольником в пространстве:

.

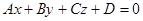Выразим z-координату точки:

.

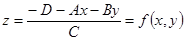Пусть

.

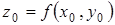Найдем z-координату для соседней точки

.

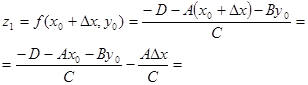
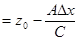Для соседнего пиксела на экране Dx = 1, тогда

,

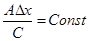отсюда следует, что z₁ = z₀ – Const. Таким образом, вычисление z-координаты соседнего пиксела сводится к одной операции вычитания.

Метод сортировки по глубине

Рассмотрим далее алгоритм удаления невидимых граней методом сортировки по глубине (авторы: Ньюэлл, Ньюэлл, Санча). Часть этого метода работает в пространстве объекта, а часть в пространстве изображения. Он также работает для параллельной проекции, то есть с учетом того что произведено перспективное преобразование.

Метод состоит из трех основных шагов:

1. Упорядочение всех многоугольников в соответствии с их наибольшими z-координатами.

2. Разрешение всех неопределенностей, которые возникают при перекрытии z-оболочек многоугольников.

3. Преобразование каждого из многоугольников в растровую форму, производимое в порядке уменьшения их наибольшей z-координаты.

Ближайшие многоугольники преобразуются в растровую форму последними и закрывают более отдаленные многоугольники, так как изображаются поверх предыдущих. Реализация пунктов 1 и 3 достаточно очевидна. Рассмотрим подробнее пункт 2.

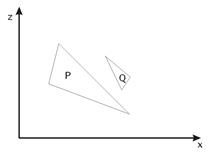
Рис. 35. 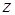-оболочки треугольников P и Q – пересекаются.

Пусть многоугольник P после упорядочения находится в конце списка, то есть является наиболее удаленным. Все многоугольники Q чьи z-оболочки перекрываются с z-оболочкой P должны проходить проверку по пяти тестам (шагам). Если на некотором шаге получен утвердительный ответ, то дальнейшие проверки прекращаются, и многоугольник P сразу преобразуется в растровую форму.

Пять тестов:

1. x-Оболочки многоугольников не перекрываются, поэтому сами многоугольники тоже не перекрываются.

2. y-Оболочки многоугольников не перекрываются, поэтому сами многоугольники тоже не перекрываются.

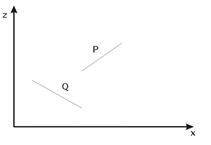
3. P полностью расположен с той стороны от плоскости Q, которая дальше от точки зрения (этот тест дает положительный ответ как показано на рис. 36 а).

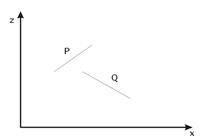
4. Q полностью расположен с той стороны от плоскости P, которая ближе к точке зрения. Этот тест дает положительный ответ как показано на рис. 36 b).

5. Проекции многоугольников на плоскости xOy, то есть на экране, не перекрываются (это определяется сравнением ребер одного многоугольника с ребрами другого).

а) b)

Рис. 36. Взаимные расположения треугольников в пространстве;
а) – положительный ответ в тесте 3; б) – положительный ответ в тесте 4.

Если во всех пяти тестах получен отрицательный ответ, то P – действительно закрывает Q. Тогда меняем P и Q в списке местами. В случае, как показано на рис. 37, алгоритм зацикливается.

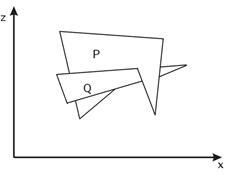
Рис. 37. Случай взаимного расположения многоугольников, когда алгоритм сортировки по глубине зацикливается.

Для избежания зацикливания вводится ограничение: многоугольник, перемещенный в конец списка (т.е. помеченный), не может быть повторно перемещен. Вместо этого многоугольник P или Q разделяется плоскостью другого на два новых многоугольника. Эти два новых многоугольника включаются в соответствующие места упорядоченного списка, и алгоритм продолжает работу.

Алгоритм художника

В алгоритме художника пространство разбивается плоскостью на два полупространства, одно содержит наблюдателя, второе не содержит. Первыми рисуются объекты второго полупространства, вторыми - с первого.