Отрицательный модус
Схема: Если А, то В Символически: ((А→В)  ~В)→ ~А
~В)→ ~А
~ В
~ А
Правильность условно-категорического умозаключения в конечном счете определяется объективным взаимоотношением между причиной и следствием, выражением которого и выступают эти умозаключения. Если есть причина (основание), то есть и следствие, а если нет следствия, то нет и причины. Основание неправильности умозаключений, этого вида в неоднозначности взаимосвязи причины и следствия: одно и то же следствие может быть результатом действия многих причин, а одна и та же причина может вызывать много различных следствий.
Разделительно-категорическое умозаключение – это умозаключение, в котором одна из посылок - разделительное суждение, а вторая посылка и заключение – категорические суждения. В зависимости от вида категорической посылки – утвердительная она или отрицательная – выделяют два модуса разделительного категорического умозаключения: (1) утверждающе–отрицающий и (2) отрицающе-утверждающий. При утверждающе-отрицающем модусе мысль направляется от утверждения одной из мыслимых альтернатив разделительной посылки к отрицанию другой. Например: «Облигации могут быть предъявительскими (А) или именными (В). Данная облигация предъявительская (А), следовательно, она не именная (~В)». При этом, должно быть выполнено требование: разделительная посылка должна представлять строгую дизъюнкцию, т.е. альтернативы должны исключать друг друга, как в данном примере.
Правильные формы утверждающе-отрицающего модуса разделительно-категорического умозаключения можно символически записать так: ((А  В)
В)  А)→ ~В; ((А
А)→ ~В; ((А  В)
В)  В)→ ~А
В)→ ~А
В отрицающе-утверждающеммодусе разделительно-категорического умозаключения мысль следует от отрицания одного из вариантов разделительной посылки к утверждению другого. Например: «Суждения могут быть простыми или сложными. Суждение «Все цветы - растения» - простое, следовательно, оно не сложное». Условием правильности этого модуса разделительно-категорического умозаключения является необходимость полной дизъюнкции, т.е. в разделительном суждении должны быть перечислены все рассматриваемые альтернативы. В случае нарушения этого условия в рассуждении возможны логические ошибки.
Правильные логические формы отрицающе-утверждающего модуса разделительно-категорического умозаключения символически можно записать так:
((А  В)
В)  ~А)→ В; ((А
~А)→ В; ((А  В)
В)  ~В)→ А
~В)→ А
Условно-разделительное умозаключение – это умозаключение с несколькими условными и одной разделительной посылками, заключение же может быть разделительным или категорическим суждением. Например:
Если вред причинен личности гражданина (А), то он подлежит возмещения в полном объеме (С)
Если вред причинен имуществу гражданина (В), то он подлежит возмещения в полном объеме (С)
Но вред причинен или личности (А) или имуществу гражданина (В)
В любом случае он подлежит возмещению в полном объеме (С).
Символически: 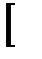 ((А→С)
((А→С)  (В→С))
(В→С))  (А
(А  В)
В)  → С
→ С
Еще пример: «Если ты будешь говорить правду (А), то тебя возненавидят богатые (С). Если ты будешь лгать (В), то тебя возненавидит простой народ (D). Но ты должен говорить правду (А) или лгать (В). Значит тебя возненавидят богатые (С) или возненавидит простой народ (D)».
Символически: 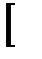 ((А→С)
((А→С)  (В→D))
(В→D))  (А
(А  В)
В)  → С
→ С  D
D
Правила, которым подчиняются условно-разделительные умозаключения, складываются из вышеотмеченных правил (требований) условно-категорического и разделительно-категорического умозаключений. Поэтому мы ограничимся тем, что выразим символически правильные формы условно-разделительных умозаключений:
(1) 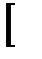 ((А→С)
((А→С)  (В→С))
(В→С))  (А
(А  В)
В)  → С
→ С
(2) 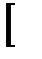 ((А→С)
((А→С)  (В→D))
(В→D))  (А
(А  В)
В)  → (С
→ (С  D)
D)
(3) 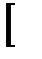 ((А→В)
((А→В)  (А→С))
(А→С))  (~В
(~В  ~С)
~С)  → ~А
→ ~А
(4) 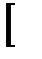 ((А→С)
((А→С)  (В→D))
(В→D))  (~С
(~С  ~D)
~D)  → (~А
→ (~А  ~В)
~В)
Определение правильности умозаключений из сложных суждений основывается на знании их правильных форм и сопоставлении логической формы проверяемого умозаключения с правильной формой данного вида умозаключения.
Для проверки правильности умозаключений из сложных суждений, не сводимых к перечисленным видам, используется табличный метод, основанный на том, что между посылками и заключением в дедуктивном умозаключении должно существовать отношение логического следования, означающее, что заключение не может быть ложным, если все посылки истинны.
Возьмем умозаключение: «Студенты этого факультета способны и прилежны. Если они прилежны, то регулярно занимаются. Значит, если они не занимаются регулярно, то они способны». Проверим, правильно ли оно. Для этого символически выразим его форму: ((А  В)
В)  (В→С))├ (~С→А), где А обозначает «студент этого факультета способен», В – «студент этого факультета прилежен», С – «студент регулярно занимается», знак «├» обозначает «следует» (перед ним записываются посылки, после него – заключение).
(В→С))├ (~С→А), где А обозначает «студент этого факультета способен», В – «студент этого факультета прилежен», С – «студент регулярно занимается», знак «├» обозначает «следует» (перед ним записываются посылки, после него – заключение).
Построим общую таблицу для этого умозаключения:
| № | А | В | С | ~С | А  В В
| В→С | ~С→А |
| и | и | и | л | и | и | и | |
| и | и | л | и | и | л | и | |
| и | л | и | л | и | и | и | |
| и | л | л | и | и | и | и | |
| л | и | и | л | и | и | и | |
| л | и | л | и | и | л | л | |
| л | л | и | л | л | и | и | |
| л | л | л | и | л | и | л |
В этой таблице для нас интересны строки, где обе посылки: (А  В) и (В→С) вместе истинны. Это строки: 1, 3, 4, 5. Смотрим, не получается ли заключение (~С→А) ложным хотя бы в одной из этих строк. Нет, заключение везде в этих строках тоже истинно. Значит умозаключение правильно.
В) и (В→С) вместе истинны. Это строки: 1, 3, 4, 5. Смотрим, не получается ли заключение (~С→А) ложным хотя бы в одной из этих строк. Нет, заключение везде в этих строках тоже истинно. Значит умозаключение правильно.
Дата добавления: 2016-04-14; просмотров: 1143;
