Виды простых суждений
По характеру признака, выражаемого предикатом суждения, выделяют три вида простых суждений:
1. Атрибутивные – суждения, в которых признак связан с наличием или отсутствием свойства. Например: «Москва – столица России», «Студенты, как правило, находчивые люди».
2. Реляционные или с отношением – это суждения, в которых признак связан с наличием или отсутствием отношения. Например: «Лето этого года теплее лета прошлого года», «Иван выше Петра», «2 в степени три равно 8».
3. Экзистенциальные или существования– это суждения, в которых выражено существование или несуществование объектов. Например: «Да, были люди в наше время», «Безвыходных ситуаций нет».
Особое значение в логике имеет деление простых суждений на виды по характеру связки (ее качеству) и характеру субъекта (его количеству, объему).
Виды суждений по качеству. Качество суждений – одна из важнейших его логических характеристик. Под ним понимается самая общая логическая форма простых суждений: утвердительная или отрицательная. Определяется качество суждений характером связки: какая она – утвердительная или отрицательная. В зависимости от этого суждения делятся на утвердительные и отрицательные. В утвердительных суждениях раскрывается наличие какой-либо связи между субъектом или предикатом. Общая формула: «S есть Р». Например: «Студенты сдали экзамен по логике», «Киты – млекопитающие». В отрицательных суждениях, наоборот, раскрывается отсутствие той или иной связи между субъектом или предикатом. Общая формула: «S не есть Р». Например: «Студенты не сдали экзамен по логике», «Киты не рыбы». Важно уяснить, что частица «не» в отрицательных суждениях относится к связке. Если же она входит в состав предиката (или субъекта), то это означает, что предикат (субъект) выражен отрицательным (а не положительным) понятием, в целом же суждение будет утвердительным. Например: «Некоторые законы бездействуют», «Профсоюзы независимы».
Виды суждения по количеству. Количество суждений – другая важнейшая характеристика суждений. Под количеством понимается логический объем субъекта. В зависимости от этого выделяются общие, частныеи единичные суждения.
Общие суждения – это суждения, в которых предикат относится ко всему объему субъекта суждения. Показателем количества (объема) субъекта выступает кванторное слово, которое в русском языке для общих суждений выражается словами: «все», «всякий», «каждый» (если суждение утвердительное) или «ни одни», «никто», «никакой» (если суждение отрицательное) и называется квантором общности – «  ». Формулы общих суждений: «Все S есть Р», «Ни одно S не есть Р». Например: «Все адвокаты - юристы», «Никто не хотел умирать». В мыслительной практике кванторное слово нередко опускается. В этом случае для определения количественной характеристики суждения его мысленно следует восстановить, поставив перед субъектом слово «каждый», если суждение утвердительное, или слово «ни один», если суждение отрицательное.
». Формулы общих суждений: «Все S есть Р», «Ни одно S не есть Р». Например: «Все адвокаты - юристы», «Никто не хотел умирать». В мыслительной практике кванторное слово нередко опускается. В этом случае для определения количественной характеристики суждения его мысленно следует восстановить, поставив перед субъектом слово «каждый», если суждение утвердительное, или слово «ни один», если суждение отрицательное.
Частные суждения – это суждения, в которых предмет относится лишь к части объема субъекта, лишь к некоторым его элементам. И в этом случае показателем объема субъекта выступает кванторное слово, называемое в современной логике квантором существования и обозначаемое символом «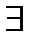 ». В русском языке он выражается такими словами как: некоторые, не все, большинство, часть и т.п. Например: «Некоторые войны справедливы», «Большинство студентов учатся добросовестно».
». В русском языке он выражается такими словами как: некоторые, не все, большинство, часть и т.п. Например: «Некоторые войны справедливы», «Большинство студентов учатся добросовестно».
Единичные суждения – это суждения, в которых субъект выражен единичным понятием, для которых в русском языке используются собственные имена или слово «это». Например: «Это – картина Шишкина», «Московский Кремль – самый красивый в мире», «Уголовный кодекс РФ давно не пересматривался». Нередко в этих случаях субъект может быть выражен собирательным понятием, например: «Большая медведица – созвездие», «Солнечная система – не единственная планетная система в нашей Галактике».
Количественная характеристика суждений имеет важное значение для уточнения, определенности наших мыслей в практике мышления. Не уточнив количество суждения нельзя осуществить ни опровержение, ни доказательство исходного суждения, ибо в зависимости от изменения количественной характеристики суждения изменяются способы его доказательства и опровержения. Так, при использовании в дискуссии, споре суждения «Человек имеет преступные наклонности», необходимо уточнение его количественной характеристики, путем приведения к одному из видов: «Этот человек имеет преступные наклонности», «Некоторые люди имеют преступные наклонности» или «Все люди имеют преступные наклонности». Понятно, что способы доказательства для них будут разными.
Суждения, у которых количество и качество может быть точно определено, называются категорическими[6] суждениями.
Качество и количество суждений тесно связаны. Поэтому в логике большое значение придается объединенной классификации категорических суждений по их количеству и качеству. При этом, единичные суждения приравниваются к общим на том основании, что те и другие высказываются обо всем объеме субъекта (Объем субъекта единичных суждений состоит из одного элемента).
Возможны четыре вида категорических суждений: общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные. Еще в средневековье в логике были введены буквенные обозначения этих четырех видов категорических суждений. Они происходят от гласных букв, входящих в латинские слова affirmo – утверждаю и nego – отрицаю. Общеутвердительные суждения получили обозначение А, общеотрицательные – Е, частноутвердительные – J, частноотрицательные – О.
Общеутвердительное суждение (А) – это суждение общее по количеству (характеру субъекта) и утвердительное по качеству (характеру связи), т.е. суждение по логической форме: «Все S есть Р». Например: «Все адвокаты - юристы», «Каждый студент нашей группы получает стипендию».
Общеотрицательное суждение (Е) – общее по количеству и отрицательное по качеству, т.е. суждение по форме: «Ни одно S не есть Р». Например: «Ни один студент нашей группы не получает стипендию».
Частноутвердительное суждение (J) – частное по количеству и утвердительное по качеству, т.е. суждение по форме: «Некоторые S есть Р». Например: «Некоторые студенты нашей группы получают стипендию».
Частноотрицательноесуждение (О) – частное по количеству, отрицательное по качеству, т.е. по форме: «Некоторые S не есть Р». Например: «Некоторые студенты нашей группы не получают стипендию».
Чтобы в практике мышления правильно оперировать суждениями, необходимо знать распределенность в них терминов – субъекта и предиката. Распределенным считается термин, взятый в полном объеме, нераспределенным – если он мыслится не в полном объеме, а частично. Полный объем понятия означает, что данное понятие полностью включается или полностью исключается из объема другого понятия.
В общеутвердительных суждениях (А): «Все S есть Р» субъект распределен, а предикат не распределен. В общеутвердительных суждениях субъект в полном объеме включается в предикат. Это означает, что общеутвердительное суждение дает информацию обо все объеме субъекта, но лишь о части объема предиката. Поэтому субъект (как понятие) распределен, а предикат нераспределен.
В общеотрицательных суждениях (Е): «Ни одно S не есть Р» - субъект и предикат распределены, поскольку каждый из терминов исключен из другого. Иными словами, суждение дает информацию обо всем объеме субъекта и обо всем объеме предиката, поэтому оба термина распределены.
В частноутвердительном суждении (J): «НекоторыеSестьР» - субъект и предикат не распределены. Субъект и предикат такого суждения только частично включаются один в другой. Суждение дает информацию лишь о части объемов своих субъекта и предиката, т.е. они оба не распределены.
В частноотрицательномсуждении (О): «НекоторыеSне естьР» - субъект нераспределен, а предикат – распределен. В таком суждении предикат в полном объеме исключен из той части объема субъекта, о которой идет речь. На этом основании предикат в частноотрицательном суждении считается распределенным, а субъект нераспределенным.
Итак: субъект распределен (берется в полном объеме) в общих суждениях, в предикат распределен в отрицательных.
3. сложные суждения: логическая структура и виды
Сложные суждения – это суждения, образованные их простых посредством той или иной логической связи. Структура сложных суждений отличается от структуры простых суждений.Основными структурообразующими элементамиздесь выступают не понятия (термины – субъект и предикат), а самостоятельныепростые суждения, внутренняя субъектно-предикатная структура которых уже не учитывается. Связь между элементами сложного суждения осуществляется с помощью логических союзов: «и», «или»; «если...то...»; «если и только если..., то»; «неверно, что...», которые близки к соответствующим грамматическим союзам, но полностью с ними не совпадают. Главное их отличие состоит в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков.
Эти типы связи простых суждений выражаются соответствующими логическими связками: конъюнкцией («и»), дизъюнкцией («или»), строгой дизъюнкцией(«либо, ...либо»), импликацией («если..., то»), эквиваленцией(тогда и только тогда, когда...», отрицанием («неверно, что...»). Логические связки обозначают символами: 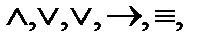 ~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
~ соответственно. Каждый из этих логических союзов, за исключением отрицания, является бинарным, т.е. соединяет только два суждения, независимо от того простые они или сами, в свою очередь, сложные, имеющие внутри себя собственные союзы.
Сложные суждения рассматриваются в логике только с точки зрения их истинностных значений, которые зависят от истинностных значений простых суждений, входящих в него, а также от характера связи этих суждений. Характер связи определяется смыслом логических союзов, который состоит в ответе на вопрос: при каких условиях сложное суждение будет истинно, а при каких – ложно. Иначе говоря, при каких сочетаниях истинности и ложности простых суждений, входящих в сложное, данный логический союз дает истинную связь, а при каких - ложную. Смысл логических союзовможно определить с помощью, так называемой истинностной таблицы, в которой на входе (см. Табл.1, столбцы 1,2) выписываются все возможные комбинации истинностных значений простых суждений (входящих в рассматриваемое сложное), а на выходе (Таблица 1 – столбцы 3 – 9) – значения сложного суждения, образованного из данных простых с помощью соответствующего логического союза.При этом, исходные простые суждения обозначают буквами: А,В,С,D..., а значения истинности символами: «и» - истино; «л» - ложно.
Таблица 1.
| NN | |||||||||
| А | В | А  В В
| А  В В
| А  В В
| А 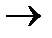 В В
| А  В В
| ~А | ~В | |
| 1. | и | и | и | и | л | и | и | л | л |
| 2. | и | л | л | и | и | л | л | л | и |
| 3. | л | и | л | и | и | и | л | и | л |
| 4. | л | л | л | л | л | и | и | и | и |
Дата добавления: 2016-04-14; просмотров: 1177;
