Изменение давления при отклонении потока на малые углы.

Ударная адиабата

В случае изоэнтропического течения справедливо:

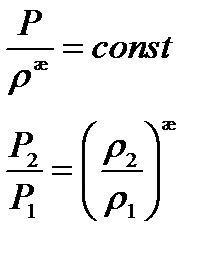
Во время скачка течение не является изоэнтропическим, тогда:

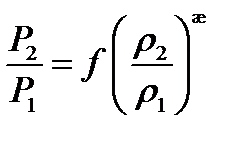
Найдем эту функцию:

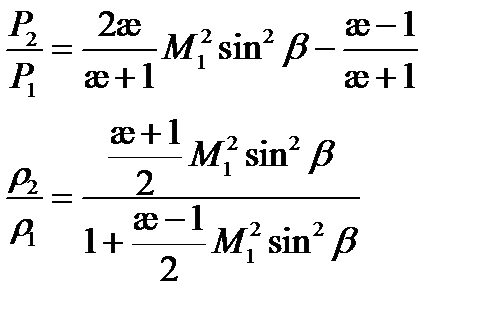
Выразим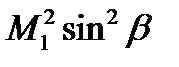

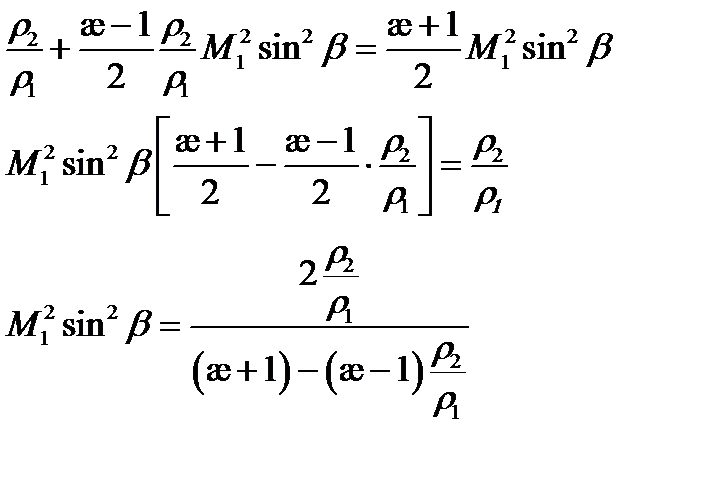
Подставим это выражение в отношение давлений:

Приведем к общему знаменателю

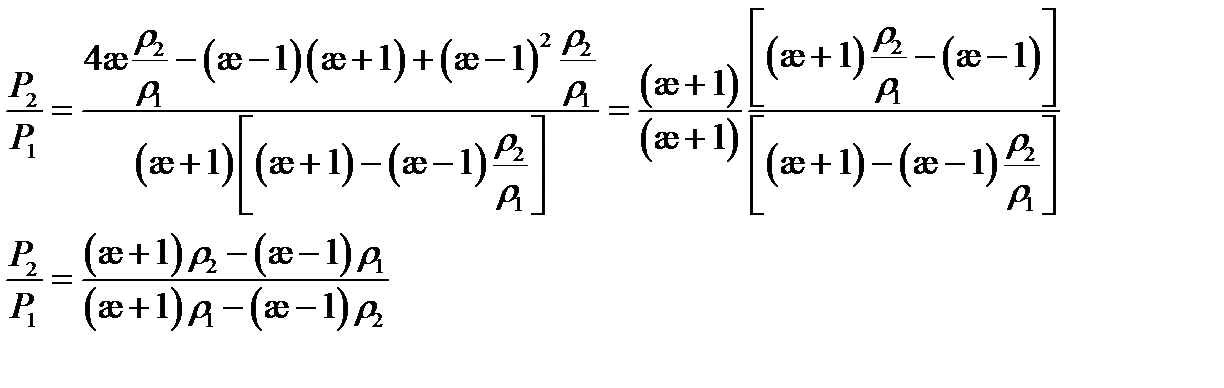
Ударная поляра.

Запишем кинематические связи между скоростями до и после скачка:

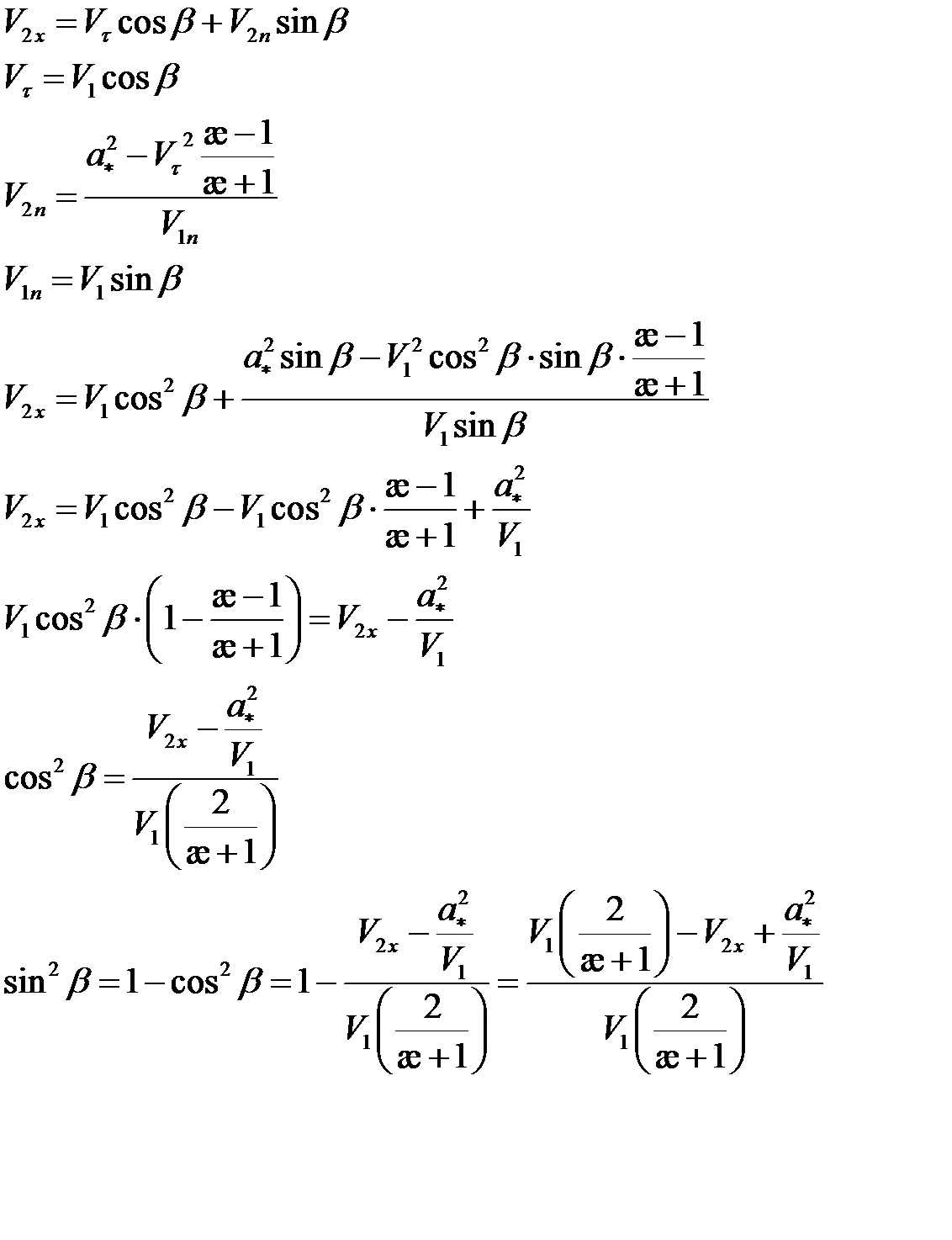
Зная синус и косинус можем найти .

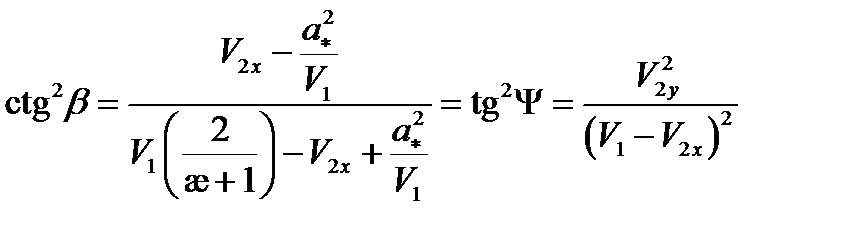
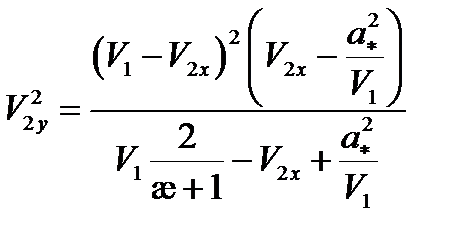- строфоида

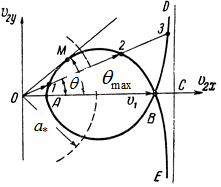
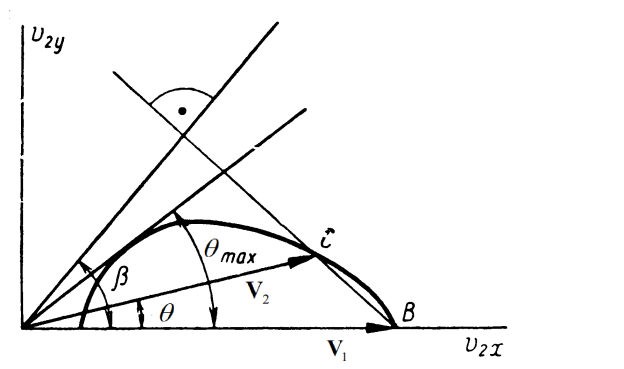Чтобы определить угол наклона скачка надо опустить перпендикуляр на продолжение секущей BC

Где θ – угол клина

Область внутри круга дает дозвуковую скорость после скачка уплотнения, а область вне круга – сверхзвуковую.

Зависимость угла наклона скачка от угла поворота потока.

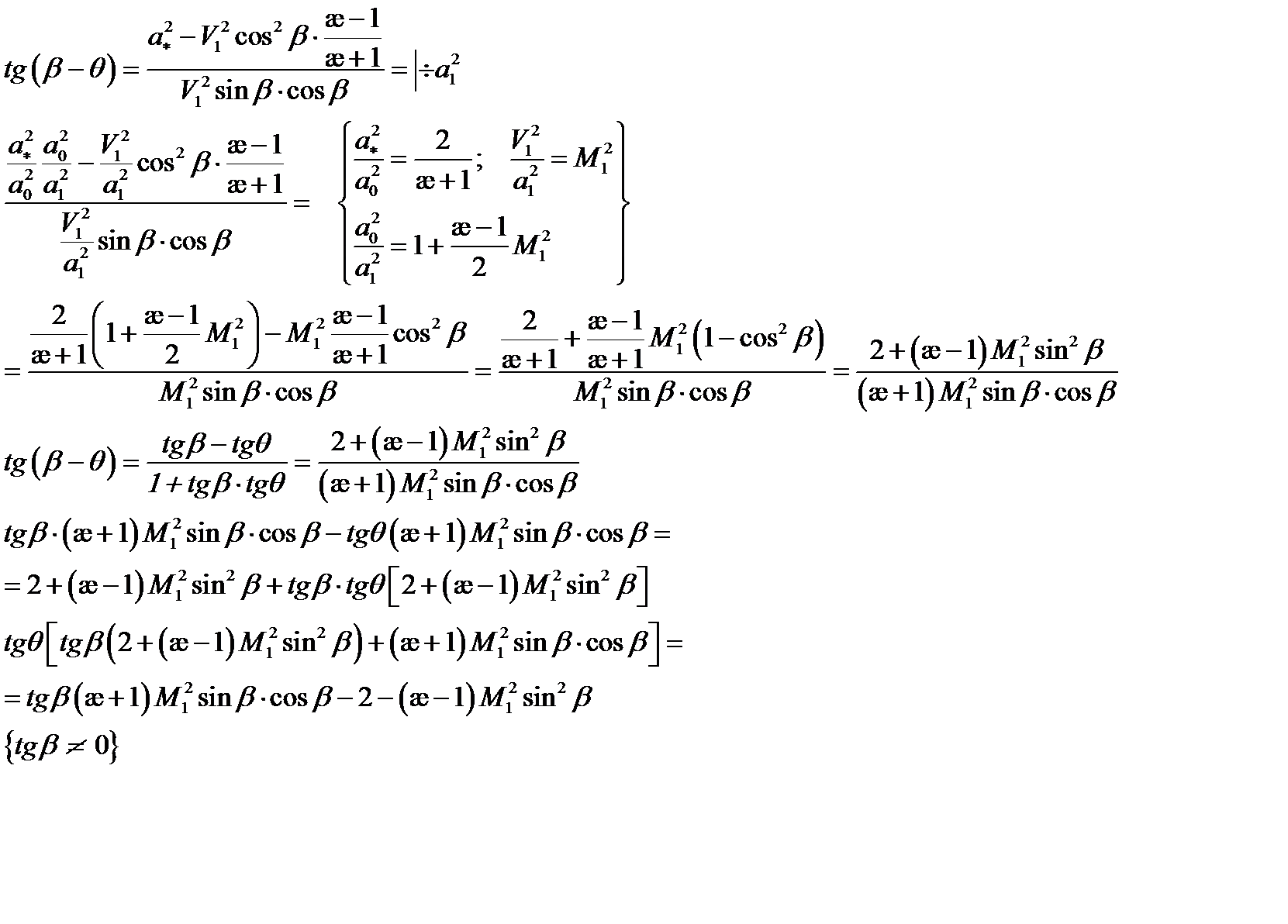
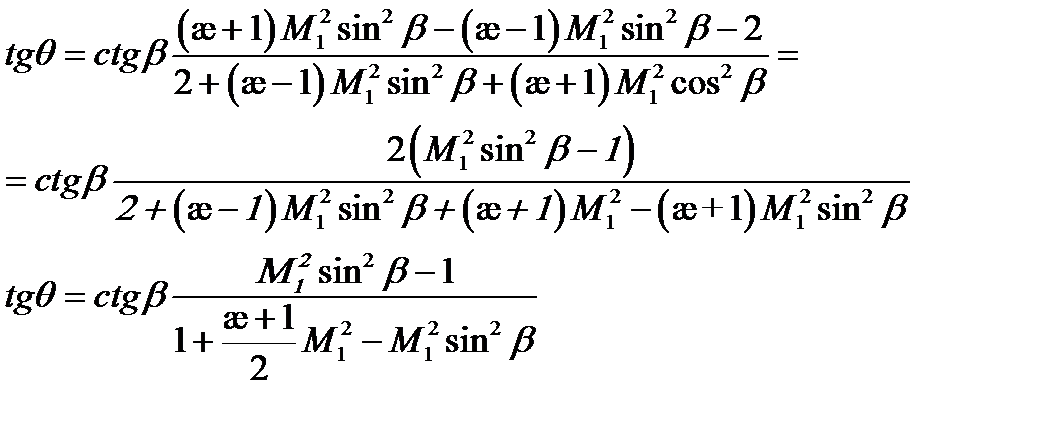
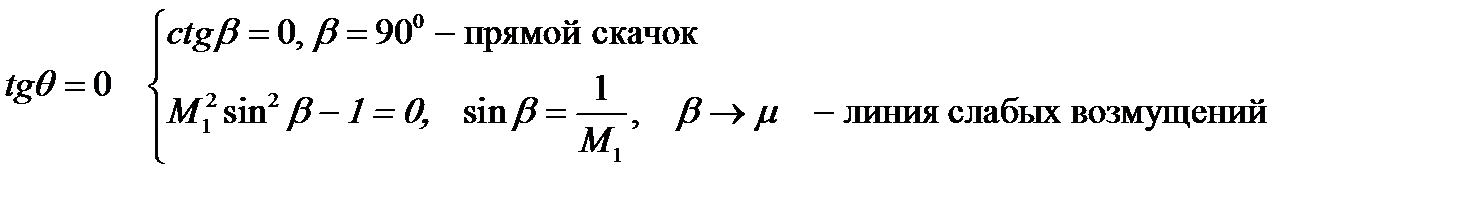
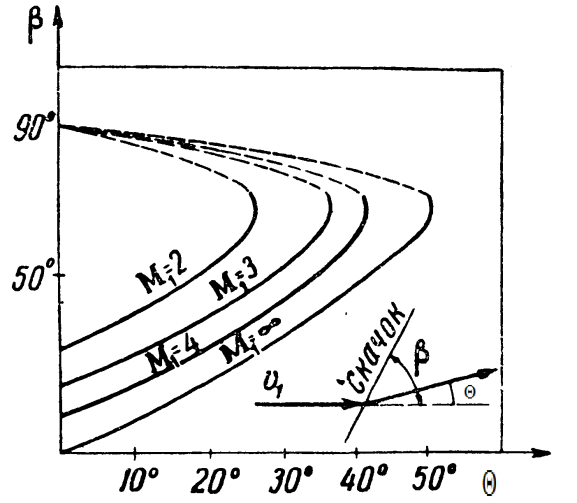
Для каждого значения Маха существует θ_max(M₁)

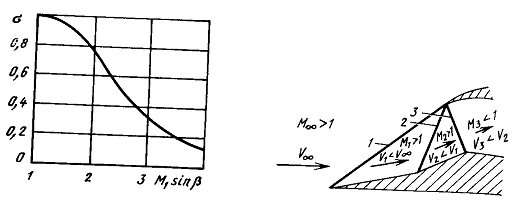
Многоскачковые воздухозаборники.

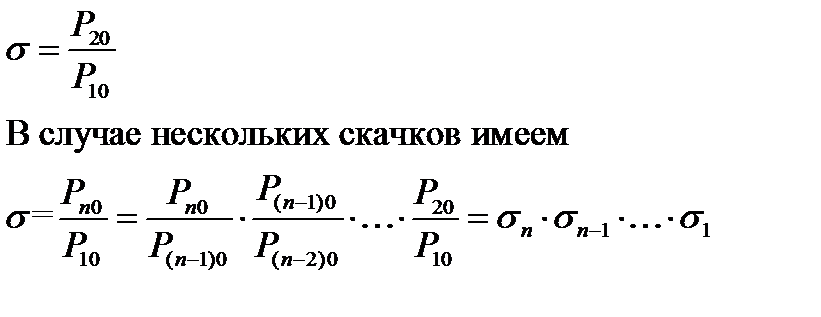
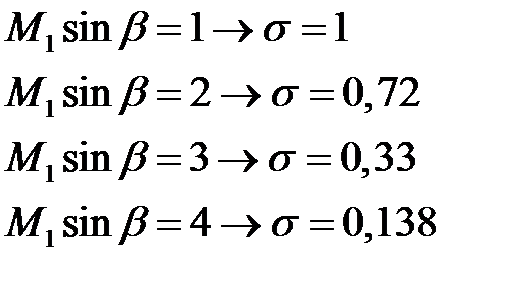
Если угол 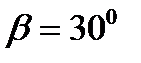то при М₁=4 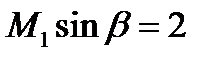, а следовательно

Достигается значительное уменьшение необратимых потерь.

Изменение давления при отклонении потока на малые углы.

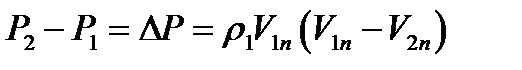
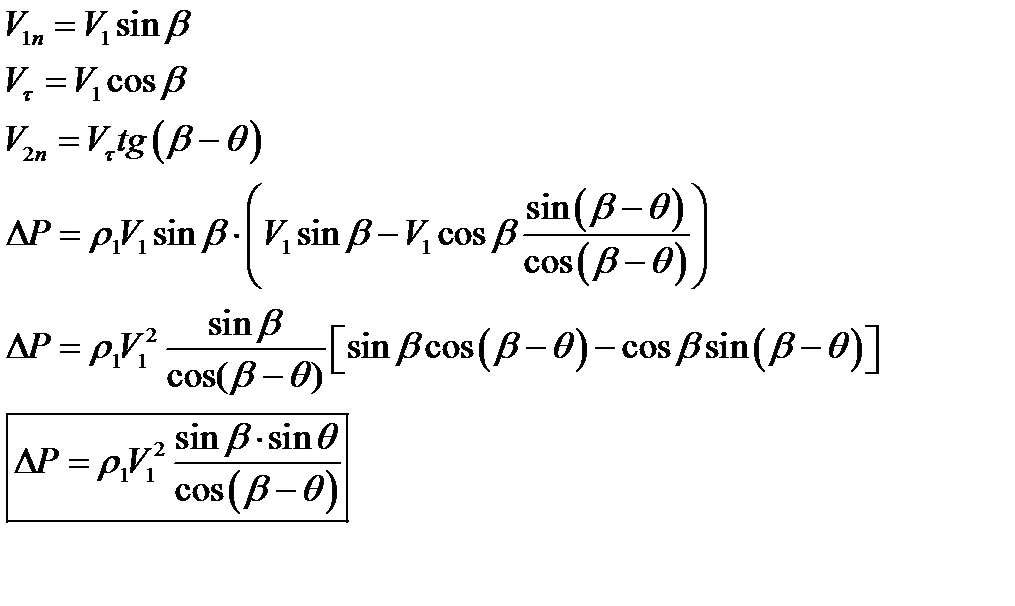
Если

При малых углах отклонения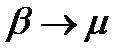

+ ставится если происходит обтекание внутреннего тупого угла.

− ставится если происходит обтекание внешнего тупого угла.