Мультипликативные эффекты, порождаемые государством. Мультипликатор государственных расходов. Налоговый мультипликатор. Мультипликатор сбалансированного бюджета.

На первом этапе анализа бюджетно-налоговой политики нам предстоит выяснить, как наш отказ от одного из допущений кейнсианской модели (относительно роли государства), повлияет на результаты, полученные при анализе этой модели.

Рис. 13.2

G

G

0 Y

(а) Рассмотрим воздействие изменения G на уровень национального доходаY

DG

DY

A

0 Y₁ Y₂ Y

=

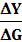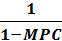
DY = 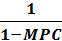DG

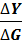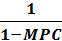K = = (1)

o K в данном случае – мультипликатор государственных расходов:

G↑Þ Y↑

G↓Þ Y↓

(б) Рассмотрим воздействие изменения T на уровень национального доходаY (рисунок 13.4).

Введем в уравнение планируемых совокупных расходов (следовательно, и в уравнение равновесия) чистые налоги T, предположив (временно), что все чистые налоги автономны, т.е. не зависят от дохода Y (T = Ta):

Y = AE

Y= Ca +MPC×(Y – T) + I + G

Y = MPC×Y + A

A = Ca - MPC×T + I + G

o Увеличение налогов уменьшает располагаемый доход на величину DT и, следовательно, уменьшает потребительские расходы по каждому уровню дохода, т.е. сдвигает кривую AE вниз на величину MPC×DT:

o В результате доход (выпуск) сокращается на величину DY:

DY = 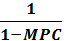(– MPC×DT)

Рис. 13.4

AE Y = AE

A₁ = Ca - MPC× T + I +G AE₁ = MPC×Y + A₁

AE₂ = MPC(Y – DT) + A₁

e₁

e₂

- MPC×DT

A DY

0 Y₂ Y₁ Y

DY= 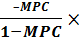DT

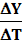
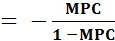(2)

o Выражение - 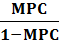называется мультипликатором налогообложения или налоговым мультипликатором. Знак «минус» означает,

что доход изменяется в направлении, противоположном изменению налогов:

T↑ÞY↓

T↓ÞY↑

(Подчеркнем, что рост трансфертов увеличивает уровень дохода, так как сокращает величину чистых налогов Т).

Как показывают уравнения (1) и (2) мультипликатор государственных расходов по абсолютной величине больше налогового мультипликатора, так как MPC в числителе налогового мультипликатора, как нам известно, меньше 1 в числителе мультипликатора государственных расходов.

Мультипликатор сбалансированного бюджета (Теорема Хаавельмо)

Итак:

· Рост государственных расходов вызывает мультипликативный рост дохода (выпуска).

· Рост налогов вызывает мультипликативное уменьшение дохода (выпуска).

Возникает вопрос:

Как изменится доход (выпуск) при сбалансированном бюджете (DG = DT)?

Условие равновесия на товарном рынке:

Y = Ca + MPC(Y – T) + I + G

Если Ca = const., I = const., MPC = const., то

DY = MPC(DY - DT) + DG.

Так как в условиях сбалансированного бюджета DG = DT, заменим DT на DG:

DY = MPC(DY - DG) + DG, или

DY - MPC×DY = – DG× MPC + DG, или

DY(1 - MPC) = DG(1 - MPC) Þ

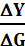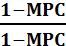= = 1 (3) Þ

∆Y = ∆G

Таким образом, мультипликатор сбалансированного бюджета равен 1.

Суть теоремы Хаавельмо:

Увеличение госрасходов при условии их финансирования за счет повышения налогов (автономных) на такую же величину (∆T =∆G) приведет к росту национального дохода (Y) на ту же величину:∆Y =∆G.

Это объясняется тем, что мультипликатор государственных расходов К по абсолютному значению больше налогового мультипликатора.

(в) Поскольку подоходный налог составляет большую часть доходов государственного бюджета, введем ставку налогообложения t (Ta – автономные налоги):

Y = Ca +MPC×(Y – tY – Ta) + I + G

Y = MPC (1 - t) Y - MPC×Ta + Ca + I + G

· если Ta, Ca, I, = const., то:

DY - MPC(1 - t)DY = DG

DY[1 – MPC(1 – t)] = DG

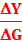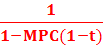= = K

· если Ca, I, G = const., то:

DY - MPC(1 - t)DY = - MPC×DTa

DY[1 – MPC(1 – t)] = - MPC×DTa

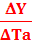= - = н.м.

Т.о., введение ставки подоходного налога:

· уменьшает значение мультипликатора автономных расходов K:

K = 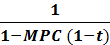(1a)

· уменьшает абсолютную величину значения налогового мультипликатора:

налоговый мультипликатор = - 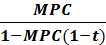(2a)

Это объясняется тем, что величина мультипликативного изменения AE зависит непосредственно не от национального дохода Y, а от располагаемого личного дохода Y(1 - t).

Еще раз сравним мультипликатор государственных расходов K и налоговый мультипликатор.

Очевидно, что K по-прежнемуимеет большее значение по абсолютной величине:

> -

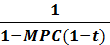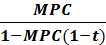
Из этого соотношения следуют два важных вывода.

ВЫВОД:

РОСТ ГОСУДАРСТВЕННЫХ РАСХОДОВ НА ВЕЛИЧИНУ XВЫЗОВЕТБОЛЬШИЙПРИРОСТ НАЦИОНАЛЬНОГО ДОХОДА, ЧЕМ СНИЖЕНИЕ РАЗМЕРА НАЛОГООБЛОЖЕНИЯ НА ТУ ЖЕ ВЕЛИЧИНУ X:

G + X Þ Y↑↑

T – X Þ Y↑

Если |∆G| = | - ∆T|, то |∆Y_(G)| > |∆Y_(-T)|

С этой точки зрения на спаде предпочтительнее использовать ↑G, при инфляции спроса - ↑T, так как при сокращении госрасходов национальный доход сократится больше, чем при увеличении налогов на ту же величину.

РЕКОМЕНДАЦИИ ДЛЯ ВЫБОРА ИНСТРУМЕНТОВ

БЮДЖЕТНО-НАЛОГОВОЙ ПОЛИТИКИ:

· НА ФАЗЕ СПАДА (ДЛЯ БОРЬБЫ С БЕЗРАБОТИЦЕЙ) предпочтительнее увеличивать госрасходы.

· НА ФАЗЕ БУМА (ДЛЯ БОРЬБЫ С ИНФЛЯЦИЕЙ) предпочтительнее увеличивать налоги.

(При этом надо иметь в виду, что бюджетно-налоговая политика как средство борьбы с инфляцией чревата опасными последствиями: проведение сдерживающей политики может привести к сокращению национального дохода (Y), т.е. борьба с инфляцией может привести к спаду и, следовательно,к росту безработицы.)