ОСНОВНОЙ ЗАКОН ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

Пусть твердое тело вращается вокруг неподвижной оси z (рис.1). При таком движении все точки тела описывают окружности, центры которых лежат на оси вращения. Поскольку векторы перемещения , скорость и ускорение различны для различных точек тела, для характеристики вращательного движения удобнее использовать угол поворота j, угловую скорость w , угловое ускорение e, одинаковые для всех точек твердого тела.

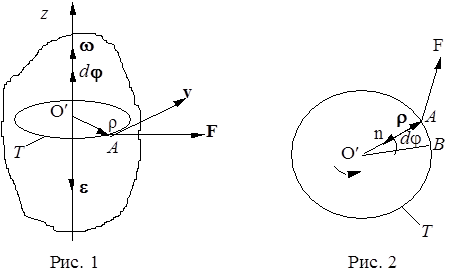
Рассмотрим движение точки A . Она движется по окружности Т, центр которой O¢ распологается на оси z . Для определения угла поворота j вектора r, определяющего положение точки А , введем неподвижную линию О¢B. Пусть rза время dt поворачивается на угол dj, в указанном направлении (рис.2). Представим малый угол поворота в виде вектора djнаправленного вдоль оси, и его направление определим следующим образом: если смотреть с конца вектора dj , вращение на угол dj видно происходящим против направления движения часовой стрелки.

Векторная величина

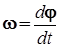(1)

называется угловой скоростью. Она направлена вдоль оси, вокруг которой вращается тело, в сторону вектора dj. Изменение вектора угловой скорости со временем характеризуется величиной

e= 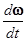, (2)

которую называют угловым ускорением.

Направление вектора e совпадает с направлением приращения вектора угловой скорости dw. Если dw > 0, то eи w направлены в одну сторону, а при dw < 0 эти векторы направлены в противоположные стороны.

Векторы линейных и угловых параметров связаны между собой соотношениями

u = [wr] ,

a_t = [er] , (3)

a_n = w² n ,

где a_t и a_n – тангенциальная и нормальная составляющие ускорения, n– единичный вектор, направленной по нормали к центру кривизны траектории .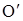

Чтобы твердое тело с закрепленной осью привести во вращательное движение, необходимо хотя бы в одной из его точек приложить внешнюю силу, не проходящую через ось вращения и не параллельную ей. Моментом силы F, приложенной в точке А перпендикулярно оси z , называется вектор

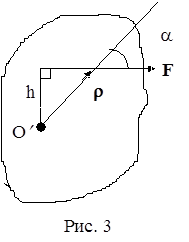
М_z = [rF], (4)

где r – вектор, указанный на рис.1 и 2. Его модуль определяется формулой

M_z =r F sin a. (5)

Здесь a - угол между векторами r и F, а величина h = r sin a - плечо силы (рис. 3). В частном случае a =p/2 получается

h = r, M_z = rF . (6)

Моментом инерции материальной точки относительно оси z называется произведение ее массы m_i на квадрат расстояния r_i от материальной точки до оси вращения

J_i = m_i r_i ² . (7)

Для определения момента инерции тела относительно оси его мысленно разбиваем на множество мелких частей. Момент инерции тела относительно оси z равен сумме моментов инерции его частей, то есть

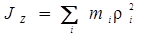. (8)

Основной закон динамики вращательного движения твердого тела вокруг неподвижной оси z записывается в виде

M_Z = e J_Z . (9)

Этот закон может быть проверен с помощью маятника Обербека.

Если сравнить (9) со вторым законом Ньютона для материальной точки

F = am , (10)

можно увидеть их сходство. Если в (10) заменить линейное ускорение aугловым ускорением e, массу m моментом инерции J_Z и силу моментом силы, то получится уравнение (9). Поэтому можно говорить, что инертность тела во вращательном движении характеризуется его моментом инерции.

Описание установки

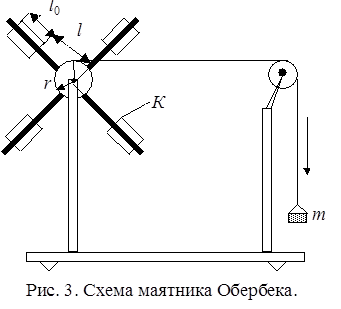
Маятник Обербека (рис.3) представляет собой крестовину из четырех стержней с делениями, прикрепленных ко втулке с осью. На стержни надеваются цилиндры К массой M, которые могут быть закреплены на разных расстояниях l от оси вращения. Шкив радиусом r насажен на ось вращения маятника. На шкив наматывается нить, перекинутая через блок. На конце нити подвешивается груз массой m. Под действием груза нить разматывается и приводит маятник в равноускоренное вращательное движение. Положение груза определяется по шкале с делениями.

Момент силы М_z, под действием которого маятник приводится во вращательное движение, определяется по формуле

M_z = F_нr , (11)

где F_н – сила натяжения нити, r – радиус шкива. Для определения силы натяжения нити запишем второй закон Ньютона P – F_н = m a , где P =mg – сила тяжести груза. Отсюда следует

F_н = m g - ma = m (g - a) . (12)

Из (11) и (12) следует

M_z = m (g – a) r .(13)

Ускорение падения груза, определяется формулой

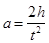(14)

где h – высота, с которой падает груз, t – время, в течение которого падает груз с высоты h. Подставив (14) в (13), получим

M_z = m 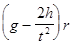. (15)

С таким же тангенциальным ускорением движутся все точки шкива, находящиеся на расстоянии r от оси вращения. Поэтому угловое ускорение шкива равно

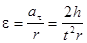. (16)