Задачи средней трудности. В1. 1. На веревочной петле в горизонтальном положении висит стержень

В1. 1. На веревочной петле в горизонтальном положении висит стержень. Нарушится ли равновесие, если справа от петли стержень согнуть?

2. Допустим, что стержень с одной стороны утолщен. Одинаковы ли массы частей стержня справа и слева от петли.

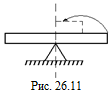В2.Однородная балка длины l и веса Р уравновешена на трехгранной призме. Изменится ли равновесие, если отрезать четвертую часть балки и положить ее на укороченный конец балки вровень с отрезком (рис. 26.11)? Если равновесие изменится, то какую силу и к какому концу балки нужно приложить, чтобы равновесие восстановилось?

В3.Бревно длиной 12 м можно уравновесить в гори­зонтальном положении на подставке, отстоящей на 3,0 м от его толстого конца. Если же подставка находится в 6,0 м от толстого конца и на тонкий конец сядет рабочий мас­сы 60 кг, бревно будет снова в равновесии. Определить мaccу бревна.

В4.Рельс длины 10 м и массы 900 кг поднимают на двух параллельных тросах. Найти силу натяжения тросов, если один из них укреплен на конце рельса, а другой – на расстоянии 1 м от другого конца.

В5.Труба массы 2,1 т имеет длину 16 м. Она лежит на двух подкладках, расположенных на расстояниях 4 и 2 м от ее концов. Какую минимальную силу надо приложить поочередно к каждому концу трубы, чтобы приподнять ее за тот или другой конец?

В6. Чему равны силы, действующие на подшипники А и В (рис. 26.12), если масса вала 10 кг, масса шкива 20 кг, |АВ| = 1,0 м, |ВС| = 0,40 м?

Рис. 26.12 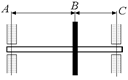Рис. 26.13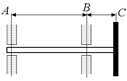

В7. Чему равны силы давления вала на подшипники А и В (рис. 26.13), если масса вала 7,0 кг, масса шкива 28 кг, |АВ| = 70 см, |ВС| = 10 см?

В8.Однородная горизонтальная балка заложена в стену так, что опирается на нее в точках А и В (рис. 26.14). Вес балки Q = 600 Н, вес груза на ее конце Р = 500 Н; размеры указаны на чертеже. Най­ти реакции стены в точках А и В.

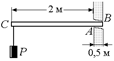
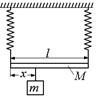
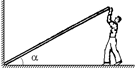
Рис. 26.14 Рис. 26.15 Рис. 26.16

В9. Однородная балка массы М и длины l подвешена за концы на двух пружинах (рис. 26.15). Обе пружины в ненагруженном состоянии имеют одинаковую длину, но жесткость левой пружины в п раз больше жесткости правой. На каком расстоянии х от левого конца балки надо подвесить груз массы т, чтобы она приняла горизонтальное положение? Считать, что п = 2.

В10.Рабочий удерживает за один конец доску, масса которой 40 кг, так, что доска образует угол 30° с гори­зонтальным направлением (рис. 26.16). Какую силу при­кладывает рабочий в случае, когда эта сила направлена перпендикулярно доске?

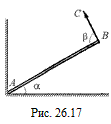В11.Тяжелая однородная доска, вес которой Р и длина l упирается одним концом в угол между стенкой и полом. К другому концу доски привязан канат (рис. 26.17). Определить натяжение каната ВС, если угол между доской и канатом b = 90°. Как меняется натяжение каната с увеличением угла a между доской и полом, если угол b остается постоянным?

Задачи трудные

С1. Шарик А укреплен на конце невесомого стержня длины l = 1,0 м, который может свободно поворачиваться вокруг оси О (рис. 26.18). Под действием силы тяжести стержень начал поворачиваться. Найти плечо В равнодействующей всех сил, действующих на шарик, относительно точки О в момент, когда стержень проходит горизонтальное положение.

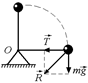
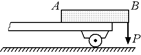
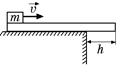
Рис. 26.18 Рис. 26.19 Рис. 26.20

С2.Однородная балка лежит на платформе так, что один конец ее свешивается с платформы (рис. 26.19). Длина свешивающегося конца равна 0,25 длины балки. На конец балки в точке В действует сила Р. При значении Р = 300 кгс противоположный конец балки А начинает подниматься. Чему равен вес балки Q?

С3.При взвешивании на неравноплечих рычажных весах вес тела на одной чашке получился равным Р₁ = 3,0 кгс, на другой Р₂ = 3,4 кгс. Определить истинный вес тела.

С4. Шайба массы т = 1,2 кг лежит на конце доски длины l = 1,5 м, противоположный конец которой выступает на h = 0,5 м за край стола (рис. 26.20). Масса доски М = 2,4 кг, коэффициент трения между доской и шайбой k = 0,40, относительно стола доска не проскальзывает. Какую минимальную скорость υ, нужно сообщить шайбе в направлении к краю стола, чтобы доска опрокинулась.

С5. Плоскую шайбу массы т = 10 кг толкнули вверх по доске длины l = 3,0 м, опирающейся на уступ на расстоянии h = 1,0 м от конца. Масса доски М = 20 кг, доска составляет угол a = 30° с горизонтом, трение между доской и шайбой отсутствует. Какую скорость υ₀ следует сообщить шайбе, чтобы нижний конец доски оторвался от пола?

С6.На правой чашке больших рычажных весов стоит человек, который уравновешен грузом, положенным на другую чашку. К середине правого плеча весов в точке С привязана веревка (рис. 26.21). Нарушится ли равновесие, если человек, стоящий на чашке весов, начнет тянуть за веревку с силой F < Р под углом a к вертикали? Вес человека Р, длина коромысла АВ = l. Весы равноплечие. Весом веревки пренебречь.

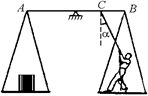
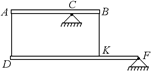
Рис. 26.21 Рис. 26.22

С7. Невесомый стержень АВ шарнирно укреплен в точке С и связан двумя нитями с однородным стержнем DF, шарнирно укрепленным в точке F (рис. 26.22). АС = 2а, СВ = a, DF = 4а, вес стержня DF равен Р. Найти натяжения нитей.

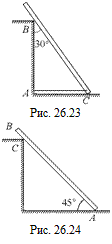С8. Однородная балка опирается о гладкий пол и о выступ В, находящийся на высоте 3,0 м над полом (рис. 26.23). Балка образует угол 30° с вертикалью и удерживается веревкой АС, протянутой у самого пола. Вычислить натяжение веревки, реакцию пола и реакцию выступа В. Вес балки 600 Н, длина 4,0 м.

С9.Однородный стержень АВ опи­рается о шероховатый пол и о гладкий выступ С (рис. 26.24). Угол наклона стержня равен 45°, расстояние АС равно 0,75 АВ. При каком коэффициенте трения стержень будет находиться в равновесии в указан­ном положении?

С10.Решить задачу С9, считая, что пол гладкий, а выступ шероховатый.

С11.У стены стоит лестница. Коэффициент трения лестницы о стену k₁ = 0,40, коэффициент трения лестницы о землю k₂ = 0,50. Центр тяжести лестницы находится на середине ее длины. Определить наименьший угол a, который лестница может образовать с горизонтом, не соскальзывая.

С12.Лестница длиной l = 4 м приставлена к гладкой стенке под углом к полу a = 60°. Максимальная сила трения между лестницей и полом F_тр = 200 Н. На какую высоту h может подняться по лестнице человек массой т = 60 кг, прежде чем лестница начнет скользить? Массой лестницы пренебречь.

С13.Лестница, вес которой Р и длина l, прислонена к гладкой вертикальной стене под углом a = 30°. Центр тяжести лестницы находится на вы­соте h от пола (рис. 26.25). Человек тянет лестницу за середину в го­ризонтальном направлении с силой F. Какой минимальной величины должна быть сила F, чтобы человек смог отодвинуть верхний конец лестницы от стены? Трение о пол настолько велико, что нижний конец лестницы не скользит.

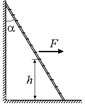
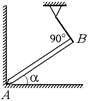
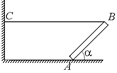
Рис. 26.25 Рис. 26.26 Рис. 26.27

С14.Кубик стоит у стены так, что одна из его граней образует угол a с полом. При каком значении коэффициента трения кубика о пол это возможно, если трение о стенку пренебрежимо мало?

С15. Однородный стержень АВ опирается одним концом в угол и удерживается за другой конец нитью (рис. 26.26). Вес стержня равен Р, а угол его наклона к горизонту равен a. Найти натяжение нити, а также давление стрежня на пол и на стену.

С16.Однородный стержень АВ опирается о шероховатый пол и удерживается в равновесии горизонтальной нитью ВС (рис. 26.27). Коэффициент трения между стержнем и полом равен 0,50. При ка­ком наклоне стержня возможно это равновесие?

С17.Нижний конец В стержня АВ укреплен шарнирно (рис. 26.28). К верхнему концу А привязана веревка АС, удержи­вающая стержень в равновесии. Найти натяжение веревки, если вес стержня Р, ÐАВС = =ÐВСА = a. Точки В и С находятся на одной вер­тикали.

С18.Стержень АО длиной 60 см (рис. 26.29) и массой 0,40 кг, укрепленный шарнирно в точке О, поддерживается нитью АС, образующей угол 45° со стерж­нем. В точке В (|АВ| = 20 см) подвешен груз массой 0,60 кг. Найти силу натяжения нити и силу реакции в точке О.

С19. Один конец горизонтальной доски упирается в стенку, к другому концу привязана нить (рис. 26.30). Второй конец нити привязан к той же точке выше доски так, что нить образует со стенкой угол a. При каком наименьшем угле a будет сохраняться равновесие, если коэффициент трения между доской и стенкой k = 0,6.

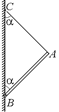
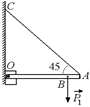
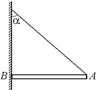
Рис. 26.28 Рис. 26.29 Рис. 26.30

С20. Один конец доски АВ массы т₁ = 0,80 кг упирается в стенку, второй конец доски удерживается нитью, закрепленной выше доски так, что нить образует со стенкой угол a = 30° (рис. 26.31). Какую минимальную массу т₂ необходимо подвесить к концу доски в точке крепления нити так, чтобы доска сохраняла горизонтальное положение?

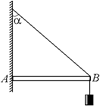
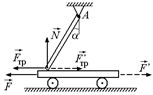
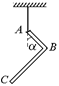
Рис. 26.31 Рис. 26.32 Рис. 26.33

С21. Стержень АВ, шарнирно закрепленный в точке А, опирается концом В на платформу (рис. 26.32). Какую минимальную силу F надо приложить, чтобы сдвинуть платформу с места? Масса стержня т, коэффициент трения стержня о платформу k и угол, образуемый стержнем с вертикалью, равен a. Трением качения колес платформы и трением в осях пренебречь.

С22.Однородные стержни АВ и ВС скреплены друг с другом в точке В (рис. 26.33). Стержень АВ вдвое короче и вдвое легче стержня ВС, угол ABC прямой. Найти угол a.

С23.Однородный брусок, у которого сторона АВ (рис. 26.34) значительно меньше, чем ВС, находится на по­верхности стола. Будем дей­ствовать по линии KL (точ­ки K и L являются середи­нами соответствую 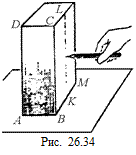щих ре­бер) с силой, параллельной поверхности стола (напри­мер, карандашом), постепен­но перемещая точку прило­жения силы от K к L. Если действовать вблизи точки K, то брусок придет в посту­пательное движение, а ес­ли вблизи точки L, то он опрокинется. Можно найти та­кую точку приложения силы, когда наблюдается переход от поступательного движения к опрокидыванию. Измерив расстояние d от этой точки до точки K и длину а ребра АВ, можно определить коэффициент трения между бруском и столом. Докажите, что коэффициент трения определяется формулой 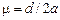. Определите таким методом коэффи­циент трения, используя, например, спичечный коробок.

С24.Каков должен быть минимальный коэффициент трения k_min материала стенок куба о горизонтальную плоскость, чтобы его можно было опрокинуть через ребро горизонтальной силой, приложенной к верхней грани? Чему должна быть равна приложенная сила F? Масса куба М.

С25.Какой минимальной силой F_min можно опрокинуть через ребро куб, находящийся на горизонтальной плоскости? Каков должен быть при этом минимальный коэффициент трения k куба о плоскость? Масса куба М.