Система предпочтительных чисел.

Теоретической базой для современной стандартизации является система предпочтительных чисел. Предпочтительными называются числа, которые рекомендуется выбирать преимущественно перед всеми другими при назначении величин параметров для вновь создаваемых изделий.

В науке и технике широко применяются ряды предпочтительных чисел, на основе которых выбирают предпочтительные размеры. Ряды предпочтительных чисел нормированы ГОСТ 8032 – 84, который разработан на основе рекомендаций ИСО. По этому стандарту установлено четыре основных десятичных ряда предпочтительных чисел (R5, R10, R20, R40) и два дополнительных (R80, R160), применение которых допускается только в отдельных, технически обоснованных случаях. Эти ряды построены в геометрической прогрессии со знаменателем φ, равным:

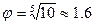• для ряда R5 (1.00; 1.60; 2.50; 4.00; …),
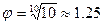• для ряда R10 (1.00; 1.25; 1.6; 2.00; …),
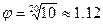• для ряда R20 (1.00; 1.12; 1.25; 1.40; …),
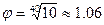• для ряда R40 (1.00; 1.06; 1.12; 1.18; …),
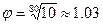• для ряда R80 (1.00; 1.03; 1.06; 1.09; …),
• для ряда R160 (1.00; 1.015; 1.03; 1.045; …).

Они являются бесконечными как в сторону убывания, так и в сторону возрастания значений.

Номер ряда предпочтительных чисел указывает количество членов ряда в десятичном интервале (от 1до10). При этом число 1.00 не входит в десятичный интервал как завершающее число предыдущего десятичного интервала (от 0.10 до1.00).

Допускается образование специальных рядов путем отбора каждого второго, третьего или n-ого числа из существующего ряда. Так образуется ряд R10/3, состоящий из каждого третьего значения основного ряда, причем начинаться он может с первого, второго или третьего значения, например:

R10 1.00; 1.25; 1.6; 2.00; 2.50; 3.15; 4.00; 5.00; 6.30; 8.00; 10.00; 12.50; …

R10/3 1.00; 2.00; 4.00; 8.00; …

R10/3 1.25; 2.50; 5.00; 10.00; …

R10/3 1.6; 3.15; 6.30; 12.50; …

Можно составлять специальные ряды с разным φ в различных интервалах ряда.

Геометрическая прогрессия имеет ряд полезных свойств, используемых в стандартизации:

1. Отношение двух соседних членов прогрессии постоянно.
2. Произведение или частное любых двух членов прогрессии является членом той же прогрессии. Это свойство используется при увязке между собой стандартизованных параметров в пределах одного ряда. Геометрические прогрессии позволяют согласовывать между собой параметры, связанные не только линейной, но и квадратичной, кубической и другими зависимостями.

По ГОСТ 8032 – 84 допускается в технически обоснованных случаях производить округление предпочтительных чисел путем применения рядов R' и R” вместо основных рядов R. В ряду R' отдельные предпочтительные числа заменены величинами первой степени округления, а в ряду R” – второй степени округления.

В радиоэлектронике часто применяются предпочтительные числа, построенные по рядам Е. Они установлены Международной электротехнической комиссией (МЭК) и имеют следующие значения знаменателя геометрической прогрессии:

• для ряда Е3 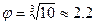; для ряда Е6 ;
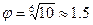• для ряда Е12 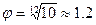; для ряда Е24 .

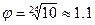При стандартизации иногда применяют ряды предпочтительных чисел, построенные по арифметической прогрессии. Арифметическая прогрессия положена в основу рядов размеров в строительных стандартах, при установлении размеров изделий в обувной и швейной промышленности и т. п.

Для выбора номинальных линейных размеров изделий (диаметров, длин, высот и т. п.) на основе рядов предпочтительных чисел разработан ГОСТ 6636 – 69 «Нормальные линейные размеры» для размеров от 0.001 до 100000 мм. Ряды в этом стандарте обозначены как Ra5, Ra10, Ra20, Ra40 и Ra80.

Государственный стандарт на предпочтительные числа имеет большое общепромышленное значение, и его необходимо применять во всех отраслях народного хозяйства при установлении параметров, числовых характеристик и количественных показателей всех видов продукции. Использование предпочтительных чисел способствует ускорению процесса разработки новых изделий, так как упрощает расчеты и облегчает выбор рациональных параметров и числовых характеристик в процессе проектирования.