Методы проецирования земной поверхности
Для составления топографических карт и планов точки земной поверхности проецируют на поверхность референц-эллипсоида или на плоскость. Проецирование на поверхность референц-эллипсоида выполняется вдоль отвесных линий. Четырехугольник аbcd, полученный проецированием на сферическую поверхность эллипсоида, называют горизонтальной проекцией четырехугольника ABCD местности (рис. 2.4).
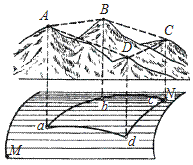 Рис. 2.4
Рис. 2.4
| 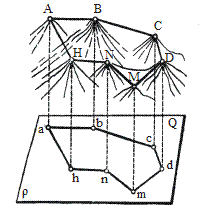 Рис. 2.5
Рис. 2.5
|
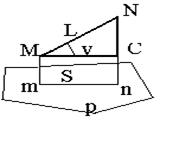 Рис. 2.6
Рис. 2.6
|
При проецировании небольших по площади участков местности, основную уровенную поверхность можно принимать за плоскость. В таком случае отвесные линии можно считать параллельными между собой и горизонтальная проекция практически преобразуется в ортогональную. Согласно рис. 2.5 отрезки ab, bc, cd,…являются ортогональными проекциями соответствующих линий AB, BC, CD,…, углы abc, bcd,…– ортогональными проекциями соответствующих углов ABC, BCD,…, а плоский многоугольник abcd – ортогональной проекцией пространственного многоугольника ABCD. Положение точек и линий местности АВ,ВС,… в ортогональной проекции определяется длинами горизонтальных проложений ab,bc,…и горизонтальными углами между ними.
Длина ортогональной проекции линии местности MN на горизон-тальную плоскость p называется горизонтальным проложением S этой линии (рис. 2.6) и вычисляется из прямоугольного треугольника MNC по формуле S = L×cos ν.
Угол ν между линией местности MN и ее ортогональной проекцией на горизонтальную плоскость S = mn,измеряют непосредственно и называют углом наклона линии. Ортогональные проекции линий на плоскость при ν ≠ 0 всегда меньше соответствующих им отрезков на физической поверхности Земли.
Дата добавления: 2016-04-11; просмотров: 1124;
