Отражение от неплоских поверхностей.

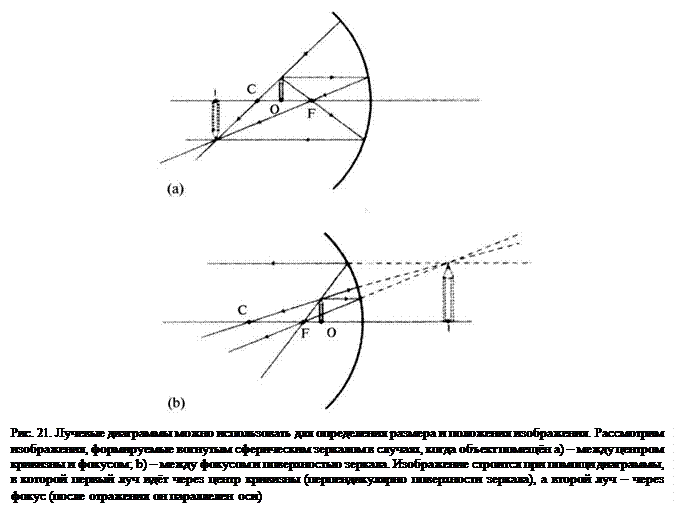
До сих пор мы рассматривали только плоские поверхности, изменяющие направление распространения луча и позволяющие создать одно или несколько изображений, но не изменяющие размер изображения. В случае изогнутой поверхности размер изображения можно уменьшить или увеличить. Эту особенность изогнутых поверхностей использовали в отражающем телескопе и отражающем микроскопе. Отражение лучей от изогнутых поверхностей иллюстрирует рис. 21. Лучи, перпендикулярные поверхности, отражаются по первоначальному пути. Лучи параллельные оптической оси после отражения сферическим или параболическим зеркалом сойдутся в одной точке на оптической оси, называемой фокусом. Положение изображения может быть определено по точке пересечения лучей. Отметим, что изображения двух объектов, расположенных с различных сторон от точки фокуса, совершенно различны (рис. 21). Обратим также внимание на то, что изображение точки, помещённой в фокус сферического зеркала, находится на бесконечности. Поэтому, если в фокус сферического зеркала поместить яркий источник света, образуется нерасходящийся (коллимированный) луч света, как в прожекторе.

Интерференция волн.

Если два некогерентных источника интенсивностью I₁ и I₂ поместить близко друг к другу, их интенсивности складываются и I_t = I₁ + I₂. Для источников, излучающих свет изотропно (одинаково), суммарная интенсивность освещения на расстоянии r даётся уравнением:

I_r = I_t / 4p r², (14)

Обычно источники света являются некогерентными, поскольку миллиарды волн, излучаемых точечными источниками, не связаны по фазе. Поэтому полная интенсивность равна средней интенсивности этих волн. Если световой луч разделить на два пучка, они будут когерентными. Если до объединения в некоторой точке лучи пройдут одинаковый оптический путь, они будут иметь одинаковую фазу. В других точках они будут иметь некоторую разницу фаз (рис. 22). Разница длины пройденного пути dl и разница фаз q связаны формулой (3).

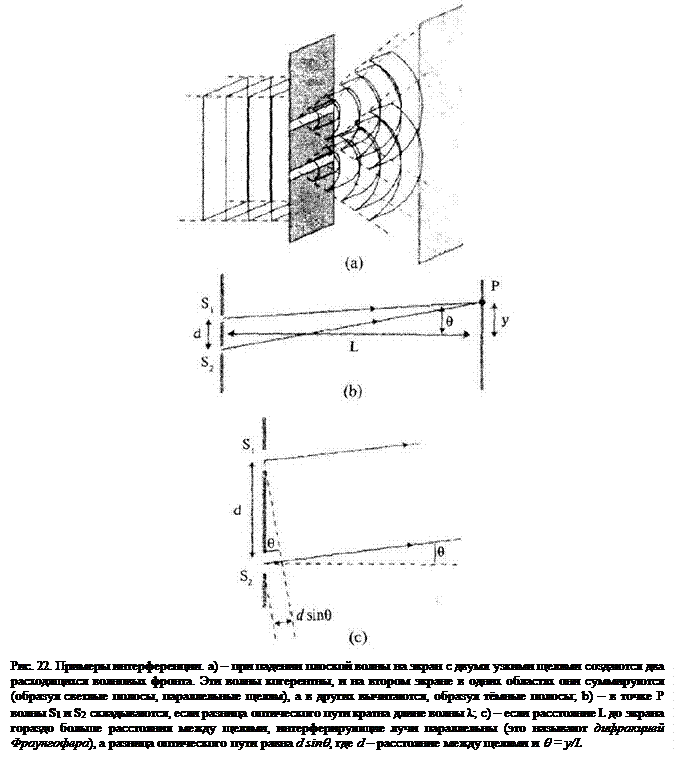
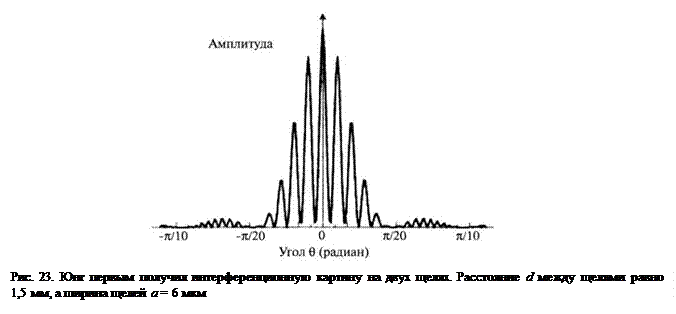
Классической иллюстрацией интерференции является эксперимент Юнга, в котором монохроматический источник (излучающий свет длиной волны l), пройдя через две узкие параллельные щели, создаёт когерентные световые волны. В результате на экране (рис. 22, а) появляются чередующиеся светлые и тёмные полосы. Светлые полосы соответствуют областям, где волны складываются в фазе, а тёмные – областям, где разность фаз равна 180°, и они вычитаются. Пусть амплитуды двух когерентных волн равны I₁ и I₂. При сложении интерферирующих волн суммарная амплитуда равна I₁ + I₂, а при вычитании – |I₁ – I₂| (рис. 23). Амплитуда суммарной волны в точке P даётся формулой:

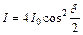, (15)

где , d – расстояние между щелями и q – угол с осью симметрии.

В интерферометре Майкельсона две когерентные волны создают с помощью посеребрённой светоделительной пластинки, через которую половина пучка проходит, а половина отражается. После деления лучи проходят различный оптический путь, а затем объединяются и создают систему интерференционных полос, как показано на рис. 24. Интерферометры играют важную роль во многих областях физики.

Светофильтры.

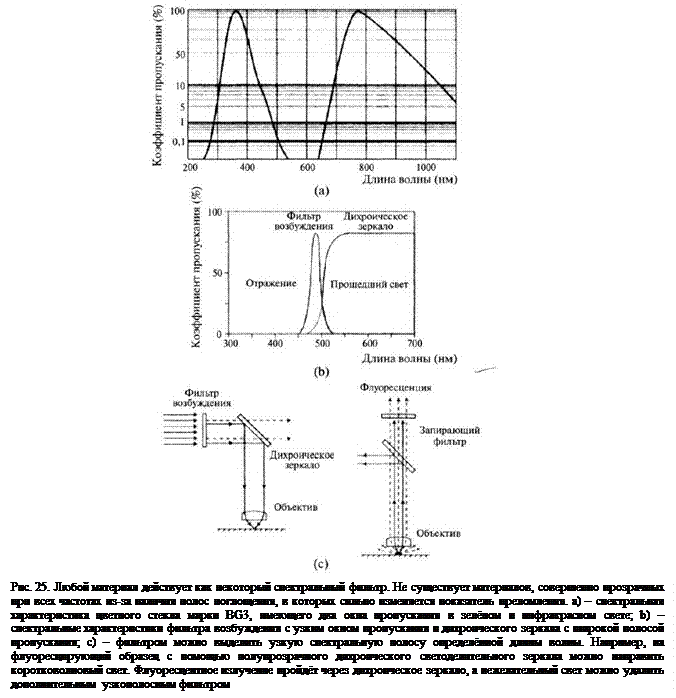
В оптических системах часто требуется монохроматический свет (одной длины волны). В театрах для получения различных цветов мощные софиты, дающие широкополосный белый свет, закрывают цветной плёнкой. Типичные спектральные характеристики светофильтров из желатина или цветного стекла показаны на рис. 25, а. Отметим, что данные светофильтры пропускают инфракрасный свет. Спектральные характеристики других светофильтров показаны на рис. 25, b, а их использование иллюстрирует рис. 25, c. Во флуоресцентной микроскопии используют «светофильтры возбуждения», выделяющие узкую спектральную полосу, а также «запирающие светофильтры», пропускающие лишь длинноволновое флуоресцентное излучение, но не пропускающие возбуждающий свет. Длина волны возбуждающего света всегда немного короче длины флуоресцентного излучения.

В исследовательской работе часто возникает потребность в узкополосных светофильтрах, пропускающих свет лишь в очень узкой полосе длин волн. Для их создания можно использовать интерференцию. Такой светофильтр можно сделать, напылив на стеклянную подложку последовательно полупрозрачное металлическое покрытие, тонкий слой диэлектрика типа криолита, снова слой металла и, наконец, закрыть систему второй стеклянной пластинкой. Если толщина диэлектрической плёнки равна d, а показатель преломления n, то при нормальном падении будут складываться волны, длина которых определяется формулой:

, (16)

где m – порядок интерференции (m = 1, 2, 3, …).

Если диэлектрическая плёнка достаточно тонкая, то в оптическом диапазоне максимальное пропускание будут иметь лишь несколько длин волн l_int. Нежелательные интерференционные максимумы можно удалить с помощью подходящего цветного стекла или желатинового светофильтра. В настоящее время можно изготовить светофильтр с очень узким диапазоном пропускания практически для любой длины волны оптического диапазона. Наиболее узкополосные светофильтры имеют ширину порядка 1,5 нм. Спектральные характеристики (коэффициент пропускания) типичных светофильтров показаны на рис. 25, b, а их использование в микроскопе иллюстрирует рис. 25, c.

В микроскопии часто используют нейтральные светофильтры. На рис. 26 показаны спектры пропускания таких светофильтров. Коэффициент пропускания нейтрального светофильтра постоянен во всём оптическом диапазоне, и его используют для уменьшения интенсивности луча. Нейтральный светофильтр можно изготовить вакуумным напылением металлической плёнки на стеклянную подложку. Светофильтры часто устанавливаются в перемещающиеся рамки или во вращающемся диске, в которых можно разместить несколько светофильтров с различными коэффициентами пропускания.

Дифракция.

Дифракция тесно связана с интерференцией. Классически её описывают как результат взаимодействия различных областей одного светового фронта, а интерференцию – со взаимодействием различных волн. Гюйгенс предположил, что световой фронт можно рассматривать как набор мельчайших вторичных когерентных источников, показанных на рис. 27. Ширина щели (сотни микрон) должна намного превышать длину волны света. После прохождения монохроматического света через щель на экране будет наблюдаться ряд светлых и тёмных полос (рис. 28).

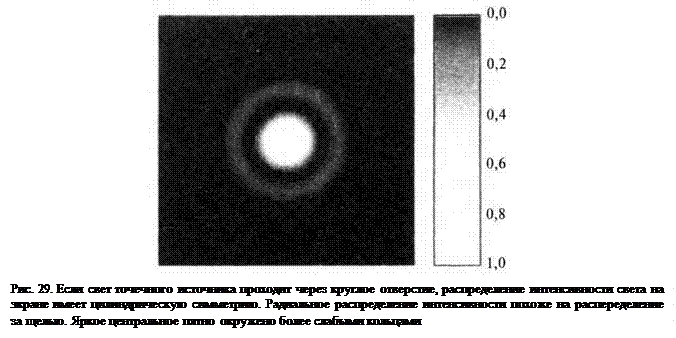
Оптические линзы имеют круглую форму, поэтому в микроскопии важнейшее значение имеет описание амплитуды световой волны за круглым отверстием. Распределение интенсивности за щелью очень похоже на радиальное распределение интенсивности за круглым отверстием. Изображение круглого отверстия на экране показано на рис. 29. Яркий дифракционный кружок в центре изображения круглого отверстия называют кружком Эри. Этот кружок окружен более слабыми кольцами.

Поглощение света.

Некоторые материалы прозрачны, и свет в них распространяется практически без поглощения. Прозрачность материала определяется степенью поглощения света. Человеческий глаз воспринимает только очень узкую часть электромагнитного спектра в диапазоне длин волн от 380 нм (фиолетовый цвет) до 750 нм (красный). «Прозрачность» материала отражает нашу субъективную оценку малых потерь в видимом диапазоне света. При других длинах волн тот же материал может быть совершенно непрозрачным. Аналогично, непрозрачный в оптическом диапазоне материал может быть совершенно прозрачным в другом диапазоне длин волн.

Существует несколько различных процессов, ответственных за поглощение света, но все они могут быть описаны простой математической моделью, показанной на рис. 30. Эта модель предполагает, что при прохождении света через тонкий слой материала толщиной dl его интенсивность уменьшается на величину, пропорциональную интенсивности падающего пучка и толщине слоя:

dI = –kIdl. (17)

Константу k называют коэффициентом поглощения (зависящим от длины волны). Интегрируя это уравнение, получим закон Бера-Ламберта:

I(l) = I₀e^–^k⁽^l⁾^L. (18)

Иногда поглощение описывают оптической плотностью материала W:

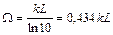, (19)

где L – толщина образца.

Хотя стекло совершенно прозрачно в видимом диапазоне, в ультрафиолетовой области оно имеет полосы поглощения, в которых сильно возрастает показатель преломления. Следовательно, величины коэффициента поглощения нужно относить к определённой длине волны. Доля света, прошедшего через плоскопараллельную пластину толщиной L, описывается формулой:

Т = (1–R₁)e^–^kL(1–R₂), (20)

где R₁ и R₂ – коэффициенты отражения на передней и задней поверхностях пластины.

Помимо поглощения, прозрачность материала зависит от степени рассеяния света. Рассеяние вызывается вариацией показателя преломления материала на неоднородностях размером меньше длины волны, например, на примесях, дефектах и т.д. Обратим внимание, что рассеяние влияет на интенсивность прошедшего светового луча совершенно аналогично поглощению. Следовательно, оно может быть описано уравнением, аналогичным формуле (20). Если N – количество рассеивающих центров в единице объёма и s_S – поперечное сечение одного центра, уменьшение интенсивности света описывается экспоненциальным законом:

(z) = I₀exp(–Ns_Sz), (21)

Джордж Стокс обнаружил, что в люминесцирующих материалах длина волны вторичного люминесцентного излучения выше длины волны падающего света. Этот эффект называют «сдвигом Стокса». Уже Максвелл понял, что этот эффект противоречит электромагнитной теории света, а объяснили его только после появления квантовой теории.

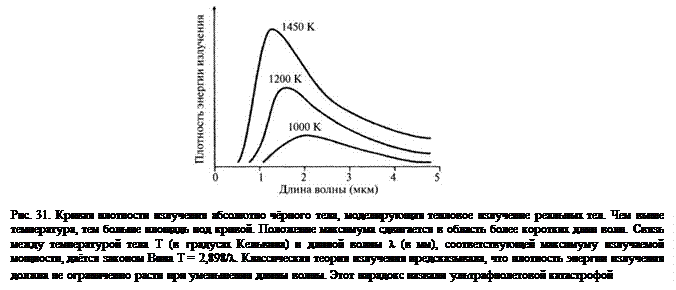
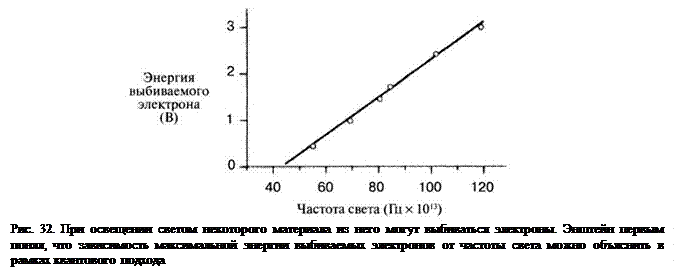
Квантовую теорию разрабатывали в течение первой четверти двадцатого столетия. Для объяснения формы спектральной кривой интенсивности излучения чёрного тела, показанной на рис. 31., Планк выдвинул гипотезу, что энергия колебаний молекул имеет вид дискретных уровней. Он также предположил, что энергия самого низкого колебательного уровня равна E_min = hf, где f – частота собственных колебаний электрических зарядов материала и h – постоянная Планка. Для объяснения фотоэффекта Энштейн предположил, что свет также излучается дискретными импульсами, которые он назвал «фотонами», и энергия фотона равна: E = hv, где v – частота света. Объяснение фотоэффекта (рис. 32) явилось триумфом фотонной теории света.

<2 3 4 5 6 78>

Дата добавления: 2016-04-11; просмотров: 1372;