Диффузное отражение.

Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения характерен, например, для гипса, песка, бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности (рис. 4.30)

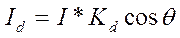
где I - интенсивность источника света, K_d— коэффициент, который учитывает свойства материала поверхности. Значение K_d находится в диапазоне от 0 до 1. Интенсивность отраженного света не зависит от расположения наблюдателя.

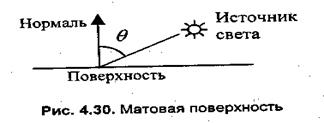
Матовая поверхность имеет свой цвет. Наблюдаемый цвет матовой поверхности определяется комбинацией собственного цвета поверхности и цвета излучения источника света.

При создании реалистичных изображений следует учитывать то, что в природе, вероятно, не существует идеально зеркальных или полностью матовых поверхностей. При изображении объектов средствами компьютерной графики обычно моделируют сочетание зеркальности и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузной и зеркальной компонент;

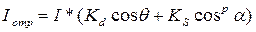
где константы K_d и K_S определяют отражательные свойства материала.

Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов q и a. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:

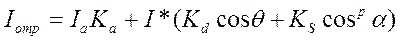
где I_a — интенсивность рассеянного света, К_a — константа.

Можно еще усовершенствовать модель отражения, если учесть то, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использование такого правила вызывает сложности; поэтому на практике часто реализуют модель, выражаемую эмпирической формулой:

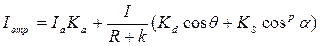
где R — расстояние от центра проекции до поверхности, k — константа.

Как определить цвет закрашивания точек объектов в соответствии с данной! моделью? Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости. Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонент. Коэффициенты K_а и K_d различны для разных компонент — они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент K_S будет одинаковым для всех компонент цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонент.

Метод Гуро

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней — такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации— чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяций цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа.

1. Вычисляются нормали к каждой грани (как векторное произведение ребер).

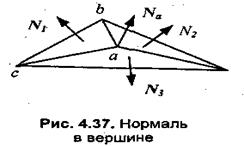
2. Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 4.37).

3. На основе нормалей в вершинах вычисляются значения интенсивностей в вершинах согласно выбранной модели отражения света ( Cosθ как скалярное произведение нормированных векторов нормали и освещения).

4. Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.

Вектор нормали в вершине (а) равен

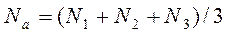
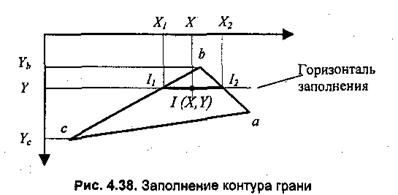
Определение интерполированных значений интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пикселя) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис, 4.38).

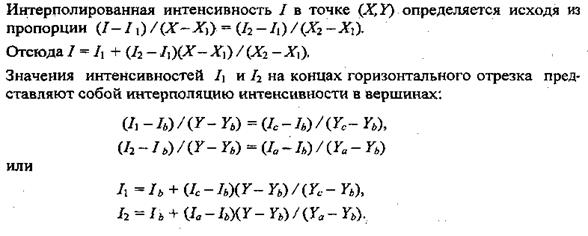
Метод Фонга

Аналогичен методу Гуро, но при использовании метода Фонга для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей.

1 Определяются нормали к граням (как векторное произведение ребер).

2 По нормалям к граням определяются нормали в вершинах. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали.

3 По направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света ( Cosθ как скалярное произведение нормированных векторов нормали и освещения).

Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'a, N'b, N'с, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям Na, Nb, Nс в вершинах а, b и с (рис. 4.39).

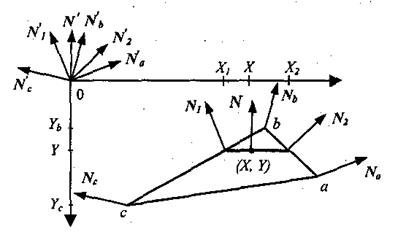
Рис. 4.39. Интерполяция векторов нормалей.

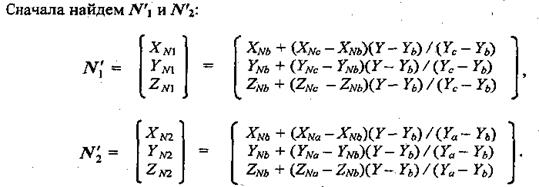
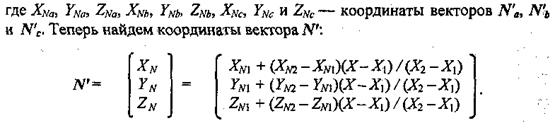
Вектор N' параллелен вектору N для нормали в точке (X, У), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.

Метод Фонга сложнее, чем метод Гуро. Для каждой точки (пикселя) поверхности необходимо выполнять намного больше вычислительных операций. Тем не менее, он дает значительно лучшие результаты, в особенности при имитации зеркальных поверхностей.

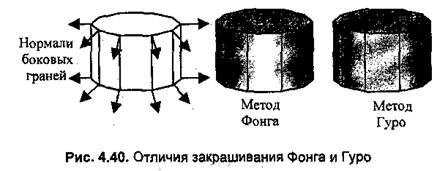Общие черты и отличия методов Гуро и Фонга можно показать на примере; цилиндрической поверхности, аппроксимированной многогранником (рис. 4.40). Пусть источник света находится позади нас. Проанализируем закрашивания боковых граней цилиндра.

На рис. 4.40 на закрашенной поверхности показаны черным цветом ребра граней— это сделано для иллюстрации особенностей закрашивания, на самом деле после закрашивания никакого черного каркаса не будет, и поверхность выглядит гладкой.

Основные отличия можно заметить для закрашивания передней грани. Она перпендикулярна направлению лучей света. Поэтому нормали в вершинах этой грани располагаются симметрично - они образовывают попарно равные по абсолютной величине углы с лучами света. Для метода Гуро это обуславливает одинаковые интенсивности в вершинах передней грани. А раз интенсивности одинаковые, то и для любой точки внутри этой грани интенсивность одинакова (для линейной интерполяции). Это обуславливает единый цвет закрашивания. Все точки передней грани имеют одинаковый цвет, что, очевидно, неправильно.

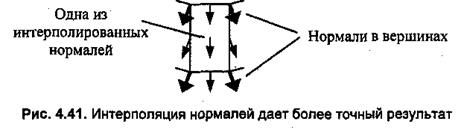Метод Фонга дает правильное закрашивание. Если интерполировать векторы нормалей передней грани, то по центру будут интерполированные нормали, параллельные лучам света (рис. 4.41).

По методу Фонга центр передней грани будет светлее, чем края.