Связь проницаемости мембран с растворимостью проникающих веществ в липидах.

Законы Фика.

Прохождение многих незаряженных веществ через мембраны подчиняется законам диффузии.

Процесс диффузии был впервые количественно описан Фиком.

Первый закон Фика поток вещества J в направлении оси х пропорционален движущей силе (градиенту концентрации dc/dx)

J=-Ddc/dx,(1)

где D — коэффициент диффузии, см^² с^-1; размерность потока — моль • см^2с^-1

Уравнение нернста-планка

J=-uRT*(dC/dx)-uCZF*(dфи/dx)

F - число Фарадея,
Z - валентность иона,
T - абсолютная температура,
R - газовая постоянная,
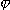- электрический потенциал на мембране.

Из сопоставления и видно, что D = RTu, где R— газовая постоянная, Т — абсолютная тем­пература, U — подвижность вещества в рассматриваемой среде. В случае стацио­нарной диффузии через тонкие мембраны dc/dx = const. Если на краях мембраны толщиной h поддерживаются постоянные концентрации (с’1 и c’₂), связанные с кон­центрациями в омывающих растворах (с1 и с2) соотношениями с’1 = гаммаc1 и с'₂ = гамма с 2, где гамма — коэффициент распределения, то поток равен

J=-D dc/dx = D(c₂ - ci)гамма/h = P(c2 – c1).

Здесь p = Dгамма/h = uRTгамма/h— проницаемость мембраны для данного вещества, см * с^-1; коэффициент у отражает липофильность вещества; и — подвижность вещества в мембране.

В общем случае нестационарной диффузии концентрация вещества в любой точке по оси х изменяется во времени.

элементарный объем с площадью 5 = 1 см² и толщиной dx

в точке х поток J, a в точке (х + dx) поток J + (dJ/dx)dx,

dJ/dx — градиент потока в напра­влении оси х.

Количество вещества, накапливающегося в рассматриваемом объеме за единицу времени, равно —{dJ/dx)dx. Количество вещества, накапливающегося в элементарном объеме, можно выразить как результат изменения концентрации во времени dc/dt, умноженной на объем V = S dx. Приравнивая эти два разных выражения, описывающие накопление вещества в объеме, получаем так называемое уравнение непрерывности

-дJ/дx = дс/дt. (2)

Подставляя (1) в (2), получаем выражение для второго закона Фика:

дc/дt = Dд²c/дx².

описывает изменение концентрации растворенного вещества в зависимости от координаты х и времени.

решение имеет вид C=c0/2(ПиDt)^0.5 exp(-x^2/4Dt) (3)

c0 — общее количество вещества, нанесенного в начальный мо­мент времени

t = 0 в точке х = 0

с — концентрация в точке х в любой момент t

Профили концентрации вещества по координате х для двух различных моментов времени, описываемые уравнением (3), приведены на рис1

Для выпуклых участков кривой д²с/дх² < 0 и, по уравнению дc/дt = Dд²c/дx²., dc/dt < 0, т. е. концентрация вещества уменьшается во времени. На удаленных от центра участках кривой d²c/dx² > 0. Следовательно, dc/dt > 0, т. е. концентрация вещества в этих участках во времени повышается. Полученный результат отражает извест­ный факт, что диффузия всегда направлена на выравнивание концентрационных градиентов.

.Профиль C, достигаемый к моменту времени t, хар пар-тром х с черточкой. C вещества на расстоянии х с черточкой умень­шается в е раз по сравнению с концентрацией в начальной точке, если показатель экспоненты в уравнении (3) равен единице: х с черточкой^2 /4Dt = 1.

Формула выше характеризует время, необходимое для диффузии, увеличивается пропорционально квадрату расстояния.

Связь проницаемости мембран с растворимостью проникающих веществ в липидах.

Коэффициент диффузии определяется размером и формой молекул. Для малых молекул в воде D ~ 10 ^-5 см^2 • с^-1. Для сферических частиц уравнение Стокса—Эйнштейна, связывающее коэффициент диффузии с радиусом частиц г и вязкостью среды ню:

D=k_Б* Т/6Пи*r*ню

Малые гидрофильные молекулы могут проникать через поры в мембране

Для проникновения неэлектролитов из воды в гидрофобную часть мембраны или узкую мембранную пору необходима частичная или полная дегидратация мо­лекул, затраты энергии на преодоление взаимодействий полярных групп моле­кулы (—СООН, —ОН, —NH2) с диполями воды. Например, значения энергии акти­вации, полученные для проникновения этиленгликоля, глицерина и эритрита через искусственные фосфолипидные мембраны, а также через мембраны изолированных клеток, близки к значениям энергии дегидратации этих соединений. Необходимость дегидратации молекул является причиной сильной температурной зависимости ко­эффициента проницаемости мембран для ряда неэлектролитов. Хотя через биоло­гические мембраны диффундируют самые разные соединения, в то же время даже сравнительно небольшие молекулы аминокислот и моносахаридов практически не проникают через мембраны большинства клеток за счет простой диффузии.