Сортировка модифицированным методом простого выбора
Этот метод основывается на алгоритме поиска минимального элемента. В массиве А(1..n) отыскивается минимальный элемент, который ставится на первое место . Для того, чтобы не потерять элемент , стоящий на первом месте , этот элемент устанавливается на место минимального . Затем в усеченной последовательности, исключая первый элемент, отыскивается минимальный элемент и ставится на второе место и так далее n-1 раз пока не встанет на свое место предпоследний n-1 элемент массива А, сдвинув максимальный элемент в самый конец.
Рассмотрим алгоритмическое решение задачи на примере сортировки некоторого массива значений по возрастанию. В соответствии с вышеописанным методом нам необходимо несколько раз выполнять операции поиска минимального элемента и его перестановку с другим элементом, то есть потребуется несколько раз просматривать элементы массива с этой целью. Количество просмотров элементов массива согласно описанию модифицированного метода простого выбора равно n-1, где n- количество элементов массива. Таким образом, можно сделать вывод, что проектируемый алгоритм сортировки будет содержать цикл, в котором будет выполняться поиск минимального элемента и его перестановка с другим элементом.
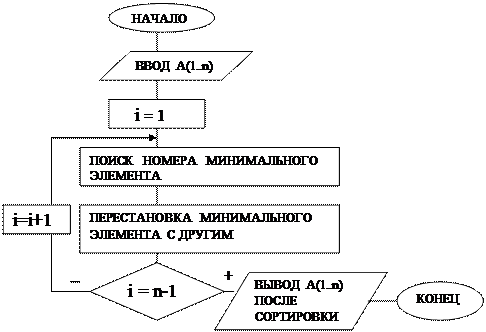 |
Обозначим через i - счетчик (номер) просмотров элементов массива и изобразим обобщенный алгоритм сортировки на рис.27.
Рис.27. Обобщенный алгоритм сортировки массива модифицированным методом простого выбора
Отметим, что для перестановки элементов местами необходимо знать их порядковые номера, алгоритм перестановки элементов массива был рассмотрен ранее (см. рис. 23). Алгоритмы ввода исходного массива и вывода этого же массива после сортировки изображены на рисунках 16 и 24 соответственно. Алгоритм поиска в массиве минимального элемента и его номера будет аналогичен рассмотренному в примере 10 алгоритму поиска максимального элемента, который представлен на рис.18. Однако, в этом алгоритме будут внесены изменения.Для того, чтобы определить какие изменения следует внести рассмотрим выполнение сортировки данным методом с акцентом на поиск минимального элемента на конкретном примере. Пусть исходный массив содержит 5 элементов
(2,8,1,3,7). Количество просмотров согласно модифицированному методу простого выбора будет равно 4. Покажем в таблице 7, как будет изменяться исходный массив на каждом просмотре.
Таблица 7. Пример сортировки
| Номер просмотра массива i | Исходный Массив | Минимальный Элемент | Переставляемый элемент | Массив после перестановки | ||
| Номер | Значе-ние | Номер | Значе-ние | |||
| (2,8,1,3,7) | (1,8,2,3,7) | |||||
| 1,(8,2,3,7) | 1,(2,8,3,7 | |||||
| 1,2,(8,3,7) | 1,2,(3,8,7) | |||||
| 1,2,3,(8,7) | 1,2,3,7,8 |
 Из данных, приведенных в таблице 7, следует, что поиск минимального значения в массиве на каждом просмотре осуществляется в сокращенном массиве, который сначала начинается с первого элемента,а на последнем просмотре массив, в котором ищется минимальный элемент начинается уже с четвертого (или n-1) элемента. При этом можно заметить, что номер первого элемента массива для каждого поиска и перестановки совпадает с номером просмотра i.
Из данных, приведенных в таблице 7, следует, что поиск минимального значения в массиве на каждом просмотре осуществляется в сокращенном массиве, который сначала начинается с первого элемента,а на последнем просмотре массив, в котором ищется минимальный элемент начинается уже с четвертого (или n-1) элемента. При этом можно заметить, что номер первого элемента массива для каждого поиска и перестановки совпадает с номером просмотра i.
Введем следующие обозначения :
К- номер минимимального элемента,
J - номер элемента массива,
М и А(К)- одно и тоже значение минимального элемента массива,
i - номер переставляемого с минимальным элемента,
А(i)- значение переставляемого элемента.
Тогда циклический алгоритм сортировки модифицированным методом простого выбора будет выглядеть следующим образом (рис.28).
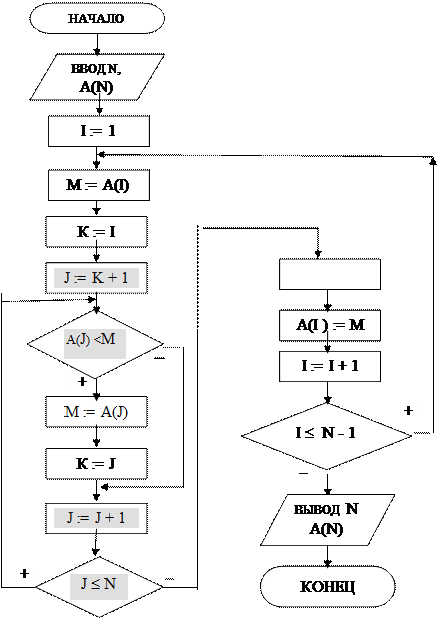 |
Рис.28. Алгоритм сотрировки массива модифицированным методом простого выбора
В этом алгоритме два цикла, внутренний цикл выделен цветом.
Дата добавления: 2016-04-06; просмотров: 2037;
