ПРИМЕНЕНИЕ ПРИНЦИПА СУПЕРПОЗИЦИИ К РАСЧЕТУ ПОЛЯ ИЗЛУЧЕНИЯ АНТЕНН
Свойства антенн принято изучать главным образом в передающем режиме, поскольку характеристики антенн в приемном режиме наиболее просто могут быть определены через характеристики тех же устройств в передающем режиме с помощью принципа взаимности.
Изучение свойств передающих антенн начнем с определения электромагнитного поля, созданного произвольной антенной, находящейся в свободном пространстве, при условии, что для этой антенны решена так называемая внутренняя задача. Для металлических антенн, это означает, что распределение электрических токов – источников электромагнитного поля – известно во всех точках антенны.
Наиболее просто и наглядно поле таких антенн рассчитывается с использованием принципа суперпозиции. Ввиду линейности уравнений Максвелла проволочную антенну длиной 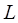 можно разбить на элементарные участки
можно разбить на элементарные участки 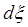 , каждый из которых при малой толщине провода можно рассматривать как элементарный электрический вибратор (ЭЭВ), и далее найти результирующее поле путем суммирования всех элементарных полей с учетом их поляризации, амплитуд и фаз.
, каждый из которых при малой толщине провода можно рассматривать как элементарный электрический вибратор (ЭЭВ), и далее найти результирующее поле путем суммирования всех элементарных полей с учетом их поляризации, амплитуд и фаз.
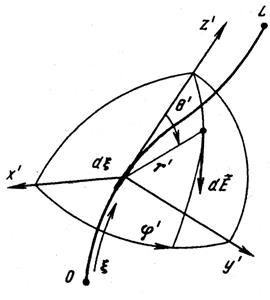
| В локальной сферической системе координат r', q', j', связанной с элементом 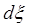 и декартовой системой x', у', z', ось z' которой совпадает с осью элементарного вибратора (рис. 1.1), комплексная амплитуда напряженности электрического поля имеет вид и декартовой системой x', у', z', ось z' которой совпадает с осью элементарного вибратора (рис. 1.1), комплексная амплитуда напряженности электрического поля имеет вид
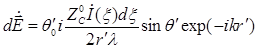 , (1.1)
где , (1.1)
где 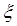 – линейная координата, отсчитываемая вдоль провода и характеризующая положение рассматриваемого элемента; – линейная координата, отсчитываемая вдоль провода и характеризующая положение рассматриваемого элемента; 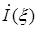 – комплексная амплитуда тока в выделенном элементе; – комплексная амплитуда тока в выделенном элементе; 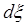 – длина ЭЭВ; – длина ЭЭВ; 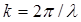 ; l – длина волны в свободном пространстве; ; l – длина волны в свободном пространстве; 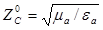 – характеристическое сопротивление среды; – характеристическое сопротивление среды; 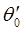 – орт сферической системы координат. – орт сферической системы координат.
|
Рис 1.1 – К расчету поля антенны
В (1.1) и далее индекс т в обозначении комплексной амплитуды опущен. Выражение (1.1) справедливо в дальней зоне выделенного элемента, т. е. при условии r' » l (реально, достаточно условия r' > 1,5l, при этом погрешность по амплитуде не превосходит 1%). Напряженность магнитного поля в дальней зоне ЭЭВ связана с (1.1) выражением
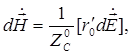 (1.2)
(1.2)
где 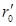 – орт сферической системы координат. Результирующее поле определяется путем геометрического суммирования (интегрирования) полей всех элементарных участков:
– орт сферической системы координат. Результирующее поле определяется путем геометрического суммирования (интегрирования) полей всех элементарных участков:
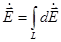 ,
, 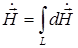 . (1.3)
. (1.3)
Принцип суперпозиции используется при расчете поля излучения и магнитных токов, каждый из элементарных участков которых можно рассматривать как излучение элементарных магнитных вибраторов (ЭМВ). Хотя магнитные токи в природе не существуют, их формальное ведение оказывается чрезвычайно полезным при анализе, например, антенн, выполненных в виде длинной узкой щели в металлическом экране.
В ряде случаев, когда распределение тока по антенне либо неизвестно, либо слишком сложно, однако из каких-либо априорных соображений известно распределение поля вблизи антенны (например, для апертурных антенн, в частности для антенн параболического типа), найти излучаемое антенной поле можно с помощью принципа эквивалентности. Согласно этому принципу излучение реальных электрических токов заменяется излучением эквивалентных поверхностных электрических и магнитных токов, распределенных в точках воображаемой произвольной поверхности S, окружающей антенну. Плотность этих токов
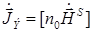 ,
, 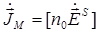 , (1.5)
, (1.5)
где n0 – единичная нормаль к поверхности S, внешняя по отношению к области, занятой антенной; 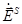 ,
, 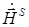 – поле в точках на поверхности S.
– поле в точках на поверхности S.
Разобьем поверхность S на элементарные площадки dS, тогда, рассматривая каждую площадку как совокупность двух элементарных излучателей – электрического и магнитного, можно найти полное поле во внешней области, суммируя поля, созданные отдельными элементами. Обычно учитывают токи только на части замкнутой поверхности S, где они наиболее существенны, причем эту часть поверхности выбирают совпадающей с фронтом волны, излучаемой антенной. В данном случае каждую элементарную площадку можно рассматривать как элемент волнового фронта – элемент Гюйгенса, электрическое поле которого и локальной системе координат r', q', j', связанной с декартовой системой x', у', z', ось z' которой совпадает с внешней нормалью 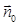 (см. рис. 1.2), при r' « l можно представить в виде
(см. рис. 1.2), при r' « l можно представить в виде
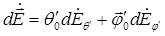 , (1.6)
, (1.6)
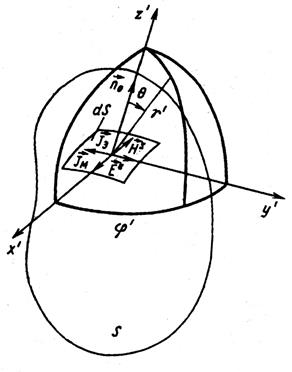 Рис 1.2 – К расчету поля элемента Гюйгенса
Рис 1.2 – К расчету поля элемента Гюйгенса
| 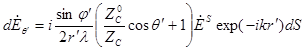 , (1.7) , (1.7)
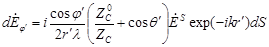 . (1.8) . (1.8)
|
Дата добавления: 2016-04-06; просмотров: 1420;
