Оптимальная фильтрация непериодического (одиночного) сигнала

Оценим возможную эффективность обнаружения непериодического сигнала при его аддитивной смеси с белым шумом. При формулировке задачи нахождения коэффициента передачи «оптимального» фильтра используются существенные требования относительно сигнала: во-первых считается известной форма сигнала f(t) и соответственно его спектр 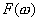, во вторых сигнал считается ограниченным во времени:

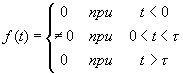(3.1)

Т.е. сигнал имеет конечную длительность.

Определение оптимальности фильтра формулируется следующим образом:

Оптимальным фильтром в задаче обнаружения одиночного импульса конечной длительности является фильтр, обеспечивающий максимальное отношение пиковой мощности сигнала к мощности шума в момент окончания импульса.

Комплексный коэффициент передачи такого оптимального фильтра прямо определяется спектром заданного, подлежащего обнаружению сигнала (т.е. его формой и длительностью 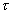) [2 ]

Так, если сигнал имеет спектр

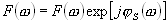(3.2)

и длительность его 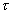, то функция

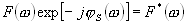
есть функция комплексно сопряженная функции спектральной плотности сигнала.

Можно показать [2], что комплексный коэффициент передачи оптимального фильтра, в приведенном выше смысле определяется так:

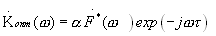
или

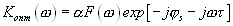(3.3)

Не воспроизводя выкладки доказательства формулы (3.3) приведенных в ряде источников (например [ 2] ), остановимся на физическом смысле результата.

Замечая, что фазовая характеристика коэффициента передачи в (3.3) есть

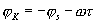
видим, что 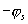— компенсирует фазовые сдвиги составляющих сдвиги спектра сигнала (3.2), что формирует «пик» импульса на выходе, а линейная функция — 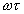обеспечивает задержку этого «пика» на время длительности сигнала, т. е. этот пик приходится на момент окончания сигнала.. Можно сказать, что обеспечивается накопление полезного сигнала на интервале всего времени существования импульса.

Формула (3.3) устанавливает также, что модуль коэффициента передачи должен совпадать с модулем спектральной плотности функции заданного сигнала, т. е. оптимальный фильтр ослабляет спектральные составляющие шума тем сильнее, чем меньше модуль 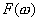, В результате полная мощность шума на выходе фильтра оказывается меньшей, чем при равномерной АЧХ.

Наконец отметим, что произвольная константа 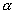размерна. При безразмерном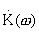 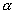имеет размерность обратной спектральной плотности сигнала.

3.2. Оценка отношения сигнал/шум при оптимальном фильтре

Будем исходить из приведенного выше выражения (3.3). Заметим, что для сигнала (импульса) сложной формы синтез оптимального фильтра является не простой задачей. По этому искомую оценку отношения сигнал/шум проведем на примере прямоугольного импульса.

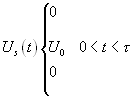(3.4)

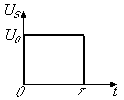
Рис.1

Будем считать, что полезный сигнал представляет собой одиночный прямоугольный импульс (3.4) длительностью 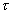и с напряжением 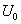, изображенный на рис 1.

Его спектральная плотность описывается функцией

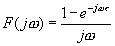и сопряженная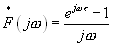

следовательно, для данного импульса в соответствии с (3.3) имеем:

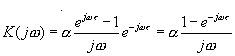(3.5).

Такой коэффициент передачи может быть обеспечен схемой рис 2.

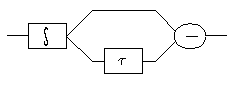
Рис.2

Содержащей идеальное интегрирующее звено ( 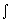), линию задержки ( 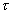) и схему вычитания .

Найдем сигнал на выходе оптимального фильтра для рассматриваемого примера ( 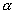=1)

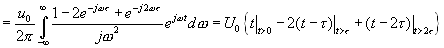(3.6).

Таким образом, импульс на выходе имеет треугольную форму с основанием 2t и максимальным значением U₀ при t=t . Оценим теперь мощность шума на выходе этого оптимального фильтра. Используем формулы (3.3) и (3.5). Положим a =1 Будем считать шум ’ белым’.

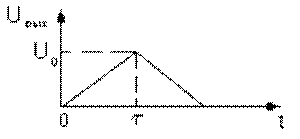
Рис.3

Представим модуль оптимального коэффициента передачи в виде

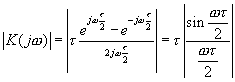(3.7)

Мощность шума на выходе фильтра в соответствии с (2.2 ) и (2.3) определиться так

(3.8).

Этот табличный интеграл [3] имеет значение: 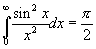. Таким образом, искомая величина мощности шума равна: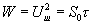

откуда искомое отношение мощности сигнала к мощности шума для данного оптимального фильтра будет:

(3.10).

а для отношения амплитуд сигнал/шум

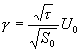(3.11).

В заключение еще раз отметим, что оптимальный фильтр, построенный по указанному выше критерию, жестко связан с полезным входным сигналом: изменение полезного входного сигнала ведет к необходимости изменения коэффициента передачи фильтра.