Видове число характеризує повнодеревність стовбура.
| Рис. 2. Співвідношення стовбура і одномірного циліндра |
1) породи;
2) розмірів стовбура;
3) повноти деревостану;
4) типу лісорослинних умов.
1.2. Різновиди видових чисел:
1) Старе видове число, яке найбільше використовується у лісогосподарській практиці:
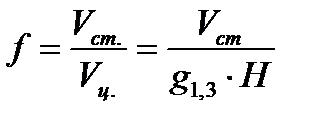 (1)
(1)
Величина видового числа коливається в межах 0,352- 0,592. У більшості дерев у віці їх господарського використання вони перебувають у межах 0,400-0,500 і лише у дерев дуже низьких можуть бути більше одиниці. Для стовбурів висотою 2,6 м видове число дорівнює одиниці.
При незмінному таксаційному діаметрі дерева і при збільшенні його висоти на кожні 2 м величина видового числа зменшується на 2 - 3 %, і навпаки: при однаковій висоті, але при збільшенні таксаційного діаметра на кожні 2 см, видове число також зменшується на 2 - 3 %.
У зв’язку з тим, що величина старого видового числа залежить від розмірів стовбура, вчені Кренке, Продан та Преслєр запропонували замінити його на нормальне видове число, а Гогенадль на істинне.
2) Нормальне видове число:
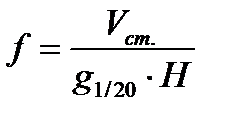 (2)
(2)
Тобто на відміну від старого видового числа, площа поперечного перерізу (g) визначається не на висоті 1,3 м, а на 1/20 висоти стовбура.
3) Істинне видове число:
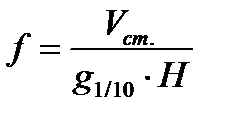 (3)
(3)
Тобто на відміну від старого видового числа, площа поперечного перерізу (g) визначається не висоті 1,3 м, а на 1/10 висоти.
Застосування нормального та істинного видових чисел ускладнено тим, що щоразу необхідно обчислювати для кожного стовбура 1/10 або 1/20 його висоти, а потім заміряти на цій висоті діаметрі визначати площу поперечного перерізу.
4) Пізніше Рінікер запропонував абсолютне видове число, при обчисленні яких площа поперечного перерізу на висоті 1,3 м приймалася за основу стовбура і циліндра, а висота зменшувалася на 1,3 м, тобто виключався відрізок стовбура від основи його до висоти 1,3 м.
Недоліком абсолютного видового числа є те, що частина стовбура розташована нижче висоти 1,3 м не враховувалася, а чим нижчий стовбур, тим більший вплив виявляє нижня частина на загальний його об’єм. Об’єм цього відрізка стовбура (від основи до висоти 1,3 м) необхідно визначати окремо і додавати до об’єму, отриманого через видове число. Внаслідок цього абсолютне видове число застосування на практиці не отримало.
1.3. Взаємозв’язок видового числа полягає в наступному:
Оскільки об’єм стовбура можна визначити за простою формулою серединного перерізу (просто формулою Губера) Vст.=γ·Н, а об’єм циліндра – Vц=g1.3·Н, а саме видове число є відношенням об’єму стовбура до об’єму циліндра, тоді маємо:
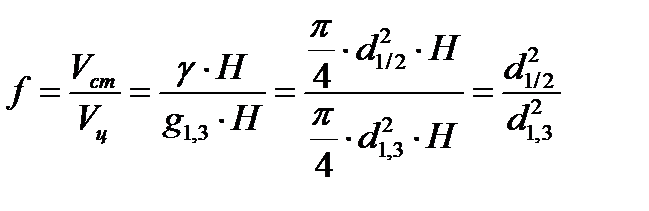
Оскільки, відношення 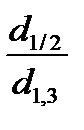 - це другий коефіцієнт форми (q2), тоді видове число буде дорівнювати квадрату другого коефіцієнта форми. Це наближена формула Вейзе:
- це другий коефіцієнт форми (q2), тоді видове число буде дорівнювати квадрату другого коефіцієнта форми. Це наближена формула Вейзе:
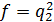 (4)
(4)
При довжині стовбурів більше 12 м видове число визначається з похибкою ±4-10%.
Для стовбура з висотою 2,6 м - d1/2 = d1,3 і видове таким чином дорівнює 1,0, а для дерев з висотою < 2,6 м d1/2 > d1,3 і видове число буде більше 1,0.
Зі збільшенням висоти стовбура видове число буде зменшуватися.
1.4. Інші способи визначення видового числа. В процесі досліджень виявлено тісний зв’язок значення старого видового числа(f) деревного стовбура з його другим коефіцієнтом форми (q2), і це дозволило встановити різницю між f і q2. Ця різниця є постійною величиною (С) для середньозбіжистих стовбурів висотою більше 15 м і в середньому визначена для окремих порід (див. табл. 3).
Таблиця 3
Значення постійної (С) у формулі Кунце
| Порода | Значення постійної | Порода | Значення постійної (С) |
| Береза повисла | 0,221 | Модрина сибірська | 0,223 |
| Бук лісовий | 0,225 | Осика | 0,217 |
| Бук східний | 0,214 | Ялина звичайна | 0,219 |
| Вільха чорна | 0,212 | Сосна звичайна | 0,211 |
| Горіх чорний | 0,213 | Сосна кедрова європейська | 0,207 |
| Граб звичайний | 0,237 | Сосна Банкса | 0,231 |
| Дуб звичайний | 0,197 | Ялиця біла | 0,209 |
| Дуб скельний | 0,253 | Ялиця сибірська | 0,211 |
| Липа серцелиста | 0,210 | Ялиця кавказька | 0,236 |
| Модрина європейська | 0,210 | Ясен звичайний | 0,201 |
1.4.1.Цю залежність вчені і практики використали для визначення наближеного значення видового числа, яка знайшла своє відображення у формулі Кунце:
f = q2 – C, (5)
де, q2 – другий коефіцієнт форми,
C – постійна, котра залежить від виду деревної породи і в меншій мірі
від лісорослинних умов та розмірів стовбура.
При довжині стовбурів більше 15 м видове число визначається з похибкою не більше ±5%.
1.4.2. Формула Шіффеля:
f = 0,66q 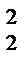 +
+ 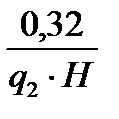 +0,140 (6)
+0,140 (6)
Середня помилка видового числа визначеного за формулою Шіффеля складає ±3%.
1.4.3. Формула Шустова:
f = 0,66q 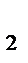 +
+ 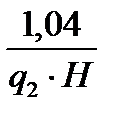 (7)
(7)
Похибка формули Шустова ±6-9%.
Дата добавления: 2016-04-02; просмотров: 6728;
