Принципы решения обратной задачи метода рефрагированных волн.

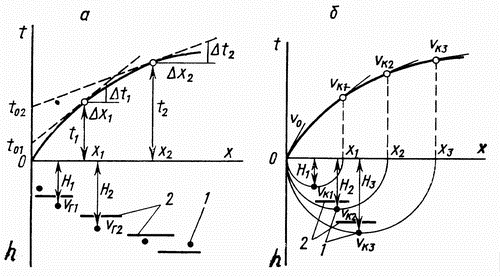
Решение обратной задачи метода рефрагированных волн (МРВ) сложнее, чем преломленных. Они сводятся к построению скоростных разрезов или полей скоростей, на которых для каждой точки разреза известна скорость. Для разных законов изменения скоростей с глубиной разработаны различные приемы построения скоростных разрезов по годографам рефрагированных волн. Рассмотрим один из простых для среды с вертикальным градиентом скорости. Она принимается за слоисто-однородную, состоящую из бесконечно тонких горизонтальных слоев, в каждом из которых скорости постоянны, а на границах возрастают скачком, но таким образом, что чем глубже слой, тем выше скорость в нем (см. рис. 4.1). Для таких разрезов можно воспользоваться решением обратной задачи МПВ над многослойной средой. На годографе рефрагированной волны выбирается несколько (до 5) точек ( 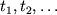) и в каждой из них проводится касательная (рис. 4.9). По пересечению касательных с осью времен определяются 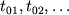, а по их наклону - кажущиеся скорости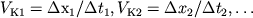

Рисунок 4.9– Годографы рефрагированных волн (а) и (б), а также построенные с их помощью скоростные разрезы: 1 - точки разреза, для которых определена скорость; 2 - изолинии скоростей

В 10.3.3 получено выражение для кажущейся скорости головной преломленной волны, которая в случае горизонтальной преломляющей границы ( 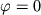) равна 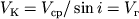(здесь применена формула 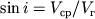). Поэтому можно записать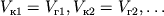

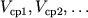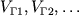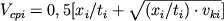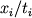За среднюю скорость в покрывающей среде над соответствующими преломляющими площадками с принимается полученное эмпирическим путем выражение , где - скорость в покрывающей толще, если считать ее неградиентной; 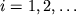По известным 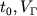и 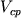можно определить глубину залегания преломляющих площадок:

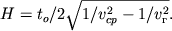
Для практического построения скоростного разреза данным методом от точек профиля, расположенных в середине между пунктом возбуждения и расчетными точками 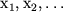, вниз откладываются глубины 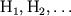и у них записываются граничные скорости 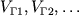Если провести изолинии, то получим скоростной разрез. Построение скоростных разрезов описанными выше способами обычно выполняется на компьютерах.