Распознаватели LR(k)-грамматик

Распознаватели LR(k)-грамматик основаны на построении дерева разбора снизу вверх и правостороннем выводе цепочек.

Определение КС-грамматика обладает свойством LR(k), k>0, если на каждом шаге выво­да для однозначного решения вопроса о выполняемом действии в алгоритме «сдвиг-свертка» расширенному МП-автомату достаточно знать содержимое верхней части стека и рассмотреть первые k символов от те­кущего положения считывающей головки автомата во входной цепочке символов.

ОпределениеГрамматика называется LR(k)-грамматикой, если она обладает свойством LR(k) для некоторого к>0.

Первая литера «L» обозначает порядок чтения входной цепоч­ки символов: слева— направо. Вторая литера «R» происходит от слова «right» и означает, что в результате работы распознавателя получа­ется правосторонний вывод.

Для того чтобы формально определить LR(k) свойство для КС-грамматик, вве­дем понятие пополненной КС-грамматики.

Определение Грамматика G' является пополнен­ной грамматикой, построенной на основании исходной грамматики G(V_T,V_N,P,S), если выполняются следующие условия:

1) грамматика G' совпадает с грамматикой G, если целевой символ S не встреча­ется нигде в правых частях правил грамматики G;

2) грамматика G' строится как грамматика G(V_T,V_N 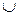{S’},P 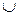{S’→S},S’), если це­левой символ S встречается в правой части хотя бы одного правила из множе­ства Р в исходной грамматике G.

Понятие «пополненной грамматики» введено исключительно с той целью, чтобы в процессе работы алгоритма «сдвиг-свертка» выполнение свертки к целевому символу пополненной грамматики S' служило сигналом к завершению алгорит­ма (поскольку в пополненной грамматике символ S' в правых частях правил ни­где не встречается).

Теперь рассмотрим формальное определение LR(k) свойства.

Если для произвольной КС-грамматики G в ее пополненной грамматике G¹ для двух произвольных цепочек вывода из условий:

1) S' =>* αAω => aβω

2) S' =>* γВх => αβу

3) FIRST(k.ω) = FIRST(k.y)

следует, что αAω = γВх (то есть α = γ, А = В и ω = у), то доказано, что граммати­ка G обладает LR(k) свойством. Очевидно, что тогда и пополненная граммати­ка G' также обладает LR(k) свойством.

Распознаватель для LR(k)-грамматик функционирует на основе управляющей таблицы Т. Эта таблица состоит из двух частей, называемых «действия» и «пере­ходы». По строкам таблицы распределены все цепочки символов на верхушке стека, которые могут приниматься во внимание в процессе работы распознавате­ля. По столбцам в части «действия» распределены все части входной цепочки символов длиной не более k (аванцепочки), которые могут следовать за считы­вающей головкой автомата в процессе выполнения разбора; а в части «перехо­ды» — все терминальные и нетерминальные символы грамматики, которые мо­гут появляться на верхушке стека автомата при выполнении действий (сдвигов или сверток).

Клетки управляющей таблицы Т в части «действия» содержат следующие дан­ные:

«сдвиг» — если в данной ситуации требуется выполнение сдвига (переноса текущего символа из входной цепочки в стек);

«успех» — если возможна свертка к целевому символу грамматики S и разбор входной цепочки завершен;

целое число («свертка») — если возможно выполнение свертки (число обозначает номер правила грамматики, по которому должна выполняться сверт­ка);

«ошибка» — во всех других ситуациях.

Действия, выполняемые распознавателем, можно вычислять всякий раз на осно­ве состояния стека и текущей аванцепочки. Однако этого вычисления можно из­бежать, если после выполнения действия сразу же определять, какая строка таблицы Т будет использована для выбора следующего действия. Тогда эту строку можно поместить в стек вместе с очередным символом и выбирать затем в мо­мент, когда она понадобится. Таким образом, автомат будет хранить в стеке не только символы алфавита, но и связанные с ними строки управляющей табли­цы Т.

Клетки управляющей таблицы Т в части «переходы» как раз и служат для выяс­нения номера строки таблицы, которая будет использована для определения вы­полняемого действия на очередном шаге. Эти клетки содержат следующие дан­ные:

целое число — номер строки таблицы Т;

«ошибка» — во всех других ситуациях.

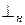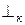Для удобства работы распознаватель LR(k)-грамматики использует также два спе­циальных символа , и . Считается, что входная цепочка символов всегда на­чинается символом 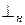и завершается символом 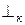. Тогда в начальном состоянии работы распознавателя символ находится на верхушке стека, а считывающая головка обозревает первый символ входной цепочки. В конечном состоянии в стеке должны находиться символы S (целевой символ) и 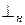, а считывающая го­ловка автомата должна обозревать символ .

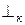Алгоритм функционирования распознавателя LR(k)-грамматики можно описать следующим образом:

Шаг 1. Поместить в стек символ 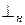и начальную (нулевую) строку управляющей таблицы Т. В конец входной цепочки поместить символ 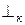. Перейти к шагу 2.

Шаг 2. Прочитать с вершины стека строку управляющей таблицы Т. Выбрать из этой строки часть «действие» в соответствии с аванцепочкой, обозреваемой счи­тывающей головкой автомата. Перейти к шагу 3.

Шаг 3. В соответствии с типом действия выполнить выбор из четырех вариантов:

«сдвиг» — если входная цепочка не прочитана до конца, прочитать и запомнить как «новый символ» очередной символ из входной цепочки, сдвинуть
считывающую головку на одну позицию вправо, иначе прервать выполнение
алгоритма и сообщить об ошибке;

целое число {«свертка») - выбрать правило в соответствии с номером, удалить из стека цепочку символов, составляющую правую часть выбранного
правила, взять символ из левой части правила и запомнить его как «новый
символ»;

«ошибка» — прервать выполнение алгоритма, сообщить об ошибке;

«успех» — выполнить свертку к целевому символу S, прервать выполнение
алгоритма, сообщить об успешном разборе входной цепочки символов, если
входная цепочка прочитана до конца, иначе сообщить об ошибке.

Конец выбора. Перейти к шагу 4.

Шаг 4. Прочитать с вершины стека строку управляющей таблицы Т. Выбрать из этой строки часть «переход» в соответствии с символом, который был запомнен как «новый символ» на предыдущем шаге. Перейти к шагу 5.

Шаг 5. Если часть «переход» содержит вариант «ошибка», тогда прервать выпол­нение алгоритма и сообщить об ошибке, иначе (если там содержится номер стро­ки управляющей таблицы Т) положить в стек «новый символ» и строку табли­цы Т с выбранным номером. Вернуться к шагу 2.

Рассмотрим примеры применения конкретных управляющих таблиц.

ПримерРаспознаватель для грамматики LR(0)

При k=0 распознающий расширенный МП-автомат совсем не принимает во внимание те­кущий символ, обозреваемый его считывающей головкой. Решение о выполняе­мом действии принимается только на основании содержимого стека автомата. При этом не должно возникать конфликтов между выполняемым действием (сдвиг или свертка), а также между различными вариантами при выполнении свертки.

Управляющая таблица для LR(0)-грамматики строится на основании понятия «левых контекстов» для нетерминальных символов: очевидно, что после выпол­нения свертки для нетерминального символа А в стеке МП-автомата ниже этого символа будут располагаться только те символы, которые могут встречаться в цепочке вывода слева от А. Эти символы и составляют «левый контекст» для А. Поскольку выбор между сдвигом или сверткой, а также между типом свертки в LR(0)-грамматиках выполняется только на основании содержимого стека, то LR(0)-грамматика должна допускать однозначный выбор на основе левого кон­текста для каждого символа.

Рассмотрим простую КС-грамматику G({a,b}, {S}, {S→aSS|b}, S). Пополненная грамматика для нее будет иметь вид G ({a,b}, {S, S’}, {S' →S, S→aSS|b}, S’). Эта грамматика является LR(0)-грамматикой. Управляющая таблица для нее приведена в табл. 3.13

Таблица 3.13 Управляющая таблица для LR(0)-грамматики

Стек	Действие	Переход
S	a	b
	Сдвиг
S	Успех, 1
a	Сдвиг
b	Свертка, 3
aS	Сдвиг
aSS	Свертка, 2

Колонка «Стек», присутствующая в таблице, в принципе не нужна для распозна­вателя. Она введена исключительно для пояснения каждого состояния стека автомата. Пустые клетки в таблице соответствуют состоянию «ошибка». Прави­ла в грамматике пронумерованы от 1 до 3 (при этом будем считать, что состоя­нию «успех» — свертке к нулевому символу — в пополненной грамматике всегда соответствует первое правило). Распознаватель работает, невзирая на текущий символ, обозреваемый считывающей головкой расширенного МП-автомата, по­этому колонка «Действие» в таблице имеет только один столбец, не помеченный никаким символом, — указанное в ней данное действие выполняется всегда для каждой строки таблицы.

Конфигурацию расширенного МП-автомата будем отображать в виде трех компонентов: не прочитанная еще часть входной цепочки символов, содержимое стека МП-автомата, последовательность номеров примененных правил грамматики (поскольку автомат имеет только одно состоя­ние, его можно не учитывать). В стеке МП-автомата вместе с помещенными туда символами показаны и номера строк управляющей таблицы, соответствующие этим символам в формате {символ, номер строки}.

Разбор цепочки aabbb.

1 (aabbb , { ,0}, ε)

2 (abbb , { ,0}{а,2}, ε)

3 (bbb , { ,0}{а,2}{а,2}, ε)

4 (bb , { ,0}{a,2}{a,2}{b,3}, ε)

5 (bb , { ,0}{a,2}{a,2}{S,4}, 3)

6 (b , { ,0}{a,2}{a,2}{S,4}{b,3}, 3)

7 (b , { ,0}{a,2}{a,2}{S,4}{S,5}, 3,3)

8 (b , { ,0}{a,2}{S,4}, 3,3,2)

9 ( , { ,0}{a,2}{S,4}{b,3}, 3,3,2)

10 ( , { ,0}{a,2}{S,4}{S,5}, 3,3,2,3)

11 ( , { ,0}{S,l}, 3,3,2,3,2)

12 ( , { ,0}{S',*}, 3,3,2,3,2,1) - разбор завершен.

Соответствующая цепочка вывода будет иметь вид (используется правосторон­ний вывод): S’ => S => aSS => aSb => aaSSb => aaSbb => aabbb.

ПримерРаспознаватель для грамматики LR(1)

Рассмотрим простую КС-грамматику G({а,b}, {S}, {S→SaSb|ε}, S). Пополненная грамматика для нее будет иметь вид G({a,b}, {S, S¹}, {S'→S, S→SaSb|ε}. S'). Эта грамматика является LR(1)-грамматикой. Управляющая таблица для нее приведена в табл. 3.14

Таблица 3.14 Управляющая таблица для LR(1)-грамматики

Стек	Действие	Переход
a	b		a	b	S
	свертка, 3		свертка, 3
S	сдвиг		успех,1
Sa	свертка, 3	свертка, 3
SaS	сдвиг	сдвиг
SaSa	свертка, 3	свертка, 3
SaSb	свертка, 2		свертка, 2
SaSaS	сдвиг	сдвиг
SaSaSb	свертка, 2	свертка, 2

Разбор цепочки abababb.

1 (abababb , { ,0}, ε)

2 (abababb , { ,0}{S,1}, 3)

3 (bababb , { ,0}{S,l}{a,2}, 3)

4 (bababb , { ,0}{S,l}{a,2}{S3h 3,3)

5 (ababb , { ,0}{S,l}{a,2}{S,3}{b,5}, 3,3)

6 (ababb , { ,0}{S,1}, 3,3,2)

7 (babb , { ,0}{S,l}{a,2}, 3,3,2)

8 (babb , { ,0}{S,l}{a,2}{S,3}, 3,3,2,3)

9 (abb , { ,0}{S,l}{a,2}{S,3}{b,5}, 3,3,2,3)

10 (abb , { ,0}{S,l}, 3,3,2,3,2)

11 (bb , { ,0}{S,l}{a,2}, 3,3,2,3,2)

12 (bb , { ,0}{S,l}{a,2}{S,3}, 3,3,2,3,2,3)

13 (b , { ,0}{S,l}{a,2}{S,3}{b,5}, 3,3,2,3,2,3)

14 Ошибка, нет данных для «b» в строке 5.

На практике LR (k)-грамматики при k > 1 не применяются. На это имеются две причины. Во-первых, управляющая таблица для LR (k)-грамматики при k > 1 бу­дет содержать очень большое число состояний, и распознаватель будет достаточ­но сложным и не столь эффективным. Во-вторых, для любого языка, определяе­мого LR(k)-грамматикой, существует LR(1)-грамматика, определяющая тот же язык. То есть для любой LR(k)-грамматики с k > 1 всегда существует эквива­лентная ей LR(1)-грамматика. Более того, для любого детерминированного КС-языка существует LR(1)-грамматика (другое дело, что далеко не всегда такую грамматику можно легко построить).