Определение грамматики операторного предшествования
ОпределениеКС-грамматика G (VN, VT, P, S) называется грамматикой операторного предшествования, если выполняются следующие условия:
1) Для каждой упорядоченной пары терминальных символов выполняется не более чем одно из трех отношений предшествования:
а) а =× b, если и только если существует правило A—>xaby ÎР или правило А->хаСbу, где a,bÎVT, A,C ÎVN, x.yÎV*;
б) а <× b, если и только если существует правило А->хаСу ÎР и вывод C=>*bz или вывод C=>*Dbz, где a,bÎVT, A,C,DÎVN, x,y,zÎV*;
в) а ×> b, если и только если существует правило А—>хСЬу ÎР и вывод C=>*za или вывод C=>*zaD, где a,bÎVT, A,C,DÎVN, x,y,zÎV*.
2) Различные правила в грамматике имеют разные правые части, e-правила отсутствуют.
3) Правила грамматики операторного предшествования не могут содержать двух смежных нетерминальных символов в правой части, т.е. в грамматике операторного предшествования G(VN,VT,P,S) не может быть ни одного правила вида: А->хВСу, где A,B,CÎVN, x,yÎV* (здесь х и у — это произвольные цепочки символов, могут быть и пустыми).
3.5.1.2.2 Построение множеств Lt(A) и Rt(A)
Принцип работы распознавателя для грамматики операторного предшествования аналогичен грамматике простого предшествования, но отношения предшествования проверяются в процессе разбора только между терминальными символами.
Для грамматики данного вида на основе установленных отношений предшествования также строится матрица предшествования, но она содержит только терминальные символы грамматики.
Для построения этой матрицы удобно ввести множества крайних левых и крайних правых терминальных символов относительно нетерминального символаА – Lt(A) или Rt(A):
Lt(A) = {t | 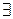 A=>*tz или
A=>*tz или 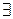 A=>*Ctz }, где tÎVT,A.CÎVN, zÎV*;
A=>*Ctz }, где tÎVT,A.CÎVN, zÎV*;
Rt(A)= {t | 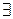 A=>*zt или
A=>*zt или 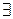 A=>*ztC }, где tÎVT, A,CÎVN, zÎV*.
A=>*ztC }, где tÎVT, A,CÎVN, zÎV*.
Тогда определения отношений операторного предшествования будут выглядеть так:
а) а =× b, если 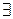 правило A→xaby ÎР или правило U->xaCby, где a,bÎVT, А,СÎVN х,уÎV*;
правило A→xaby ÎР или правило U->xaCby, где a,bÎVT, А,СÎVN х,уÎV*;
б) а <× b, если 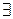 правило А→хаСу ÎР и bÎ Lt (C), где a,bÎVT, A,CÎVN, x,yÎV*;
правило А→хаСу ÎР и bÎ Lt (C), где a,bÎVT, A,CÎVN, x,yÎV*;
в) а ×> b, если 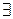 правило A→xCby ÎР и aÎ Rt(C), где a,bÎVT, A,CÎVN, x,yÎV*.
правило A→xCby ÎР и aÎ Rt(C), где a,bÎVT, A,CÎVN, x,yÎV*.
В данных определениях цепочки символов x,y,z могут быть и пустыми цепочками.
Для нахождения множеств Lt(A) и Rt(A)предварительно необходимо выполнить построение множеств L(A) и R(A), как это было рассмотрено ранее. Далее для построения Lt(A) и Rt(A) используется следующий алгоритм:
Шаг 1. 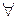 AÎVN:
AÎVN:
Rt0(A){t | 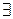 A→ytB или A→yt, tÎVT, BÎVN, yÎV*;
A→ytB или A→yt, tÎVT, BÎVN, yÎV*;
Lt0(A){t | 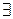 A→Bty или A→ty, tÎVT, BÎVN, yÎV*;
A→Bty или A→ty, tÎVT, BÎVN, yÎV*;
Для каждого нетерминального символа А ищем все правила, содержащие А в левой части. Во множество L(A) включаем самый левый терминальный символ изправой части правил, игнорируя нетерминальные символы, а во множество R(А) - самый крайний правый терминальный символ из правой части правил. Переходим к шагу 2.
Шаг 2. 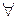 AÎVN:
AÎVN:
Rti(A) = Rti-1(A) 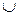 Rti-1 (B),
Rti-1 (B), 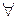 В Î (R(A)
В Î (R(A) 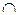 VN),
VN),
Lti(А) = Lti-1(A) 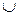 Lti-1(B),
Lti-1(B), 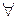 В Î (L(A)
В Î (L(A) 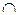 VN).
VN).
Для каждого нетерминального символа А: если множество L(A) содержит нетерминальные символы грамматики А', А", ..., то его надо дополнить символами входящими в соответствующие множества L t(А’), L t(A"), ... и не входящими в L t(А). Ту же операцию надо выполнить для множеств R(A) и Rt(А).
Шаг З. Если 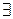 AÎVN : Rti(A)
AÎVN : Rti(A) 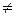 Rti-1(Aили Lti(А)
Rti-1(Aили Lti(А) 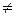 Lti-1(A), то i:=i+1 и вернутсяк шагу 2, иначе построение закончено: Rt(A) = Rti(A) и Lt(A) = Lti(А).
Lti-1(A), то i:=i+1 и вернутсяк шагу 2, иначе построение закончено: Rt(A) = Rti(A) и Lt(A) = Lti(А).
Если на предыдущем шаге хотя бы одно множество Rt(A) или Lt(A) для некоторого символа грамматики изменилось, то надо вернуться к шагу 2, иначе построение закончено.
Для практического использования матрицу предшествования дополняют символами  и
и  ( начало и конец цепочки). Для них определены следующие отношения предшествования:
( начало и конец цепочки). Для них определены следующие отношения предшествования:
 <· a,
<· a, 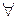 aÎVT, если
aÎVT, если 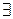 S=>*ax или
S=>*ax или 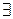 S=>*Cax, где S,CÎVN, xÎV* или если aÎ Lt(S);
S=>*Cax, где S,CÎVN, xÎV* или если aÎ Lt(S);
 ·> а,
·> а, 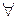 aÎVT, если
aÎVT, если 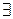 S=>*xa или
S=>*xa или 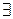 S=>*xaC, где S,CÎVN, xÎV* или если aÎ Rt(S).
S=>*xaC, где S,CÎVN, xÎV* или если aÎ Rt(S).
Здесь S — целевой символ грамматики.
Матрица предшествования служит основой для работы распознавателя языка, заданного грамматикой операторного предшествования. Поскольку она содержит только терминальные символы, то, следовательно, будет иметь меньший размер, чем аналогичная матрица для грамматики простого предшествования. Следует отметить, что напрямую сравнивать матрицы двух грамматик нельзя — не всякая грамматика простого предшествования является грамматикой операторного предшествования, и наоборот.
3.5.1.2.4 Алгоритм «сдвиг-свертка» для грамматики операторного предшествования
Этот алгоритм в целом похож на алгоритм для грамматик простого предшествования, рассмотренный выше. Он также выполняется расширенным МП-автоматом и имеет те же условия завершения и обнаружения ошибок. Основное отличие состоит в том, что при определении отношения предшествования этот алгоритм не принимает во внимание находящиеся в стеке нетерминальные символы и при сравнении ищет ближайший к верхушке стека терминальный символ. Однако после выполнения сравнения и определения границ основы при поиске правила в грамматике нетерминальные символы следует, безусловно, принимать во внимание.
Алгоритм состоит из следующих шагов.
Шаг 1. Поместить в верхушку стека символ  , считывающую головку — в начало входной цепочки символов.
, считывающую головку — в начало входной цепочки символов.
Шаг 2. Сравнить с помощью отношения предшествования терминальный символ, ближайший к вершине стека (левый символ отношения), с текущим символом входной цепочки, обозреваемым считывающей головкой (правый символ отношения). При этом из стека надо выбрать самый верхний терминальный символ, игнорируя все возможные нетерминальные символы.
Шаг 3. Если имеет место отношение <· или =×, то произвести сдвиг (перенос тощего символа из входной цепочки в стек и сдвиг считывающей головки на один шаг вправо) и вернуться к шагу 2. Иначе перейти к шагу 4.
Шаг 4. Если имеет место отношение ·>, то произвести свертку. Для этого надо найти на вершине стека все терминальные символы, связанные отношение («основу»), а также все соседствующие с ними нетерминальные символы (при определении отношения нетерминальные символы игнорируются). Если терминальных символов, связанных отношением =×, на верхушке стека нет, то в качестве основы используется один, самый верхний в стеке терминальный символ стека. Все (и терминальные, и нетерминальные) символы, составляющие основу надо удалить из стека, а затем выбрать из грамматики правило, имеющее правую часть, совпадающую с основой, и поместить в стек левую часть выбранного правила. Если правило, совпадающее с основой, найти не удалось, то необходимо прервать выполнение алгоритма и сообщить об ошибке, иначе, если разбор не закончен, то вернуться к шагу 2.
Шаг 5. Если не установлено ни одно отношение предшествования между текущим символом входной цепочки и самым верхним терминальным символом в стеке, то надо прервать выполнение алгоритма и сообщить об ошибке.
Конечная конфигурация данного МП-автомата совпадает с конфигурацией при распознавании цепочек грамматик простого предшествования.
Пример
Дано: G({(, ), ^, &, ~, a}, {S, T, E, F}, P, S), где
P: S→S^T | T
T→T&E | E
E→~E | F
F→ (E) | a
Построить: распознаватель для G.
Таблица 3.10 - Построение множеств L(A) и R(A)
| i | Li(A) | Ri(A) |
| L0(S)={S, T} L0(T)={T, E} L0(E)={~, F} L0(F)={(, a} | R0(S)={T} R0(T)={E} R0(E)={E, F} R0(F)={), a} | |
| L1(S)={S, T, E} L1(T)={T, E, ~, F} L1(E)={~, F, (, a} L1(F)={(, a} | R1(S)={T, E} R1(T)={E, F} R1(E)={E, F, ), a} R1(F)={), a} | |
| L2(S)={S, T, E, ~, F, (, a} L2(T)={T, E, ~, F, (, a} L2(E)={~, F, (, a} L2(F)={(, a} | R2(S)={T, E, F, ), a} R2(T)={E, F, ) a} R2(E)={E, F, ), a} R2(F)={), a} | |
| L3(S)={S, T, E, ~, F, (, a} L3(T)={T, E, ~, F, (, a} L3(E)={~, F, (, a} L3(F)={(, a} | R3(S)={T, E, F, ), a} R3(T)={E, F, ) a} R3(E)={E, F, ), a} R3(F)={), a} |
Таблица 3.11 - Построение множеств Lt(A) и Rt(A)
| i | Lt(A) | Rt(A) |
| Lt0(S)={^} Lt0(T)={&} Lt0(E)={~} Lt0(F)={(, a} | Rt0(S)={^} Rt0(T)={&} Rt0(E)={~} Rt0(F)={), a} | |
| Lt1(S)={^, &, ~, (, a } Lt1(T)={&, ~, (, a} Lt1(E)={~, (, a} Lt1(F)={(, a} | Rt1(S)={^, &, ~, ), a} Rt1(T)={&, ~, ), a} Rt1(E)={~, ), a} Rt1(F)={), a} | |
| Lt2(S)={^, &, ~, (, a } Lt2(T)={&, ~, (, a} Lt2(E)={~, (, a} Lt2(F)={(, a} | Rt2(S)={^, &, ~, ), a} Rt2(T)={&, ~, ), a} Rt2(E)={~, ), a} Rt2(F)={), a} |
Таблица 3.12 - Матрица операторного предшествования символов грамматики
| Символы | ^ | & | ~ | ( | ) | а | 
|
| ^ | ·> | <· | <· | <· | ·> | <· | ·> |
| & | ·> | ·> | <· | <· | ·> | <· | ·> |
| ~ | ·> | ·> | <· | <· | ·> | <· | ·> |
| ( | <· | <· | <· | <· | =× | <· | |
| ) | ·> | ·> | ·> | ·> | |||
| а | ·> | ·> | ·> | ·> | |||

| <· | <· | <· | <· | <· |
Для ^ находящейся в правиле вывода слева от нетерминала Т, во множество Lt(Т) входят символы &, ~, (, a , значит в строке матрицы для ^ ставим знак меньшего предшествования в позициях этих символов. С другой стороны этот символ ^ находится справа от S. Во множество Rt(S) входят символы ^, &, ~, ), a, значит знак большего предшествования ставится в столбце для ^ в позициях этих символов. Символы ( и ) в правиле вывода находятся радом, поэтому в позиции этих символов ставится знак равного предшествования (игнорируя нетерминал Е).
Дата добавления: 2016-03-27; просмотров: 2062;
