Семинар. Постоянное магнитное поле. Магнетики

Задача 7.1.1, №9

Дано: R₀/R = 3/2; n = 3; μ(r); j А/м². Определить: B(r) = ? H(r) = ? J(r) = ? I_мол;I_{мол.пов.=} ?-сила соответственно молекулярного и поверхностных молекулярных токов и их направление; j_молZ, j_{мол.повZ} - проекциина e_Z орт в цилиндрической системе координат векторовj_мол, j_{мол.пов} соответственноплотностеймолекулярногои поверхностных молекулярных токов_. и их направление.

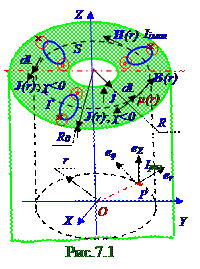
направленного по e_r орту из O начала координат основной OXY плоскости цилиндрическойсистемы координат в проекцию на неё P точки, в которой определяется μ(r) магнитная проницаемость и имеет следующий вид:

μ(r) = (35R³ - 8r³) /8R³ (R² + r²),(1.1) где (рис.7.1.1) R ≤ r ≤ 3R/2.

Циркуляция (7.124) из раздела 7.2 "Магнитное поле в веществе" вектора H(r)напряжённостимагнитного поля поокружности(рис.7.1) радиусом rв области пространства, занятого магнетиком, равнарезультирующему I_рез макроскопическому или току проводимости через поверхность S площадью, которую охватывает эта окружность r радиусом.

Охватываемая окружностьюr радиусом поверхность - это кольцос внутреннимR радиусом и внешнимr радиусом. По нормалик поверхности этого кольца(рис.7.1)течётток проводимости с j А/м² модулёмвектора j плотности.

Результирующаясила I_рез тока проводимости через поверхностькольца с внутреннимR радиусом и внешним rрадиусом имеет следующий вид: I_рез = jπ(r² - R²) А, (1.2) где (рис.7.1.1) R ≤ r ≤ 3R/2.

Модуль H(r)вектора H(r) напряжённостимагнитного поля при циркуляции поокружности(рис.7.1) радиусом r постоянен, поэтому с учётом(1.2) модуль H(r) вектора H(r) напряжённостимагнитного поля в функции от радиуса rокружности, охватывающей кольцевуюповерхность магнетика с внутреннимрадиусом R и внешнимрадиусомr, имеет следующий вид: H2πr = I_рез ↔ H2πr = jπ(r² - R²) ↔ H(r) = j(r² - R²)/2r А/м,(1.3) где (рис.7.1.1) R ≤ r ≤ 3R/2.

Модуль H(r)вектора H(r) напряжённостимагнитного поля на внутреннейH_{|r = R} сr = R радиусом и внешнейH_{|r = 3R/2} сr = 3R/2 радиусомповерхностяхтрубчатогопроводника из магнетика с учётом(1.3) имеет следующий вид: H_{|r = R} = 0 А/м; H_{|r = 3R/2} = j(5/12)R А/м. (1.4) Согласно (7.127) из раздела 7.2 "Магнитное поле в веществе"связь модуля H(r)вектора

H(r) напряжённостис модулем B(r) вектора B(r)индукции магнитного поля имеет следующий вид:

B =μ₀μH.(1.5) Подставляем (1.1) магнитную μ(r) проницаемостьмагнетика, из которой изготовлентрубчатыйпроводник, а также (1.3) модуль H(r)вектора H(r)напряжённостимагнитного поля в (1.5) и получаем следующее выражение для модуля B(r) вектора B(r)индукции магнитного поля в функции от rрадиуса окружности, охватывающей кольцевуюповерхность магнетика с внутреннимR радиусоми внешнимr радиусом: B(r) = jμ₀[(35R³ - 8 r³)(r² - R²)]/16R³ кг/с²А(Тл),(1.6) где (рис.7.1) R ≤ r ≤ 3R/2.

Модуль B(r) вектора B(r)индукции магнитного поля на внутреннейB| _{r = R} сr = Rрадиусом и внешнейB| _{r = 3R/2} сr = 3R/2 радиусомповерхностяхтрубчатогопроводника из магнетика с учётом(1.6) имеет следующий вид: B_{|r = R} = 0 кг/с²А(Тл); B_{|r = 3R/2} = jμ₀(5/12)R кг/с²А(Тл).(1.7)

Проекция (7.115) из раздела 7.2 "Магнитное поле в веществе" J _l(r) навектор dl обхода Г контура вектора J(r)намагниченности магнетика(рис.7.1.1), из которой изготовлентрубчатыйпроводник,в функции от r радиуса окружности, охватывающей кольцевуюповерхность магнетика с внутреннимрадиусом R и внешнимрадиусомr и S площадью, имеет следующий вид:

J _l = (μ - 1)H,(1.8)

где J _l(r) может быть положительной, когда μ >1 для парамагнетикови ферромагнетиков, и может быть отрицательной, когда μ < 1 для диамагнетиков.

Подставляем (1.1) магнитнуюμ(r) проницаемостьмагнетика, из которой изготовлентрубчатыйпроводник, а также (1.3) модуль H(r)вектора H(r)напряжённостимагнитного поля в (1.8) и получаем следующее выражение для проекции J _l(r) навектор dl обхода Г контура вектора J(r)намагниченности магнетика(рис.7.1), из которой изготовлентрубчатыйпроводник,в функции от r радиуса окружности, охватывающей кольцевуюповерхность магнетика с Rвнутренними rвнешнимрадиусами: J_l = j[(27R³ - 8 r³)(r² - R²)]/16R³ rА/м,(1.9) где (рис.7.1) R ≤ r ≤ 3R/2; J_l(r) = J_φ(r) -проекцияJ _l(r) навектор dl обхода Г контура вектора

J намагниченности магнетикаравна J_φ(r) проекции на e_φ орт в цилиндрическойсистемекоординат этого вектора J намагниченности магнетика(рис.7.24), т.е. J_φ(r)= J_l(r), поскольку эти dl и e_φ векторы коллинеарныи направлены в одну сторону.

Проекция J _l(r) навектор dl обхода Г контура вектора J(r)намагниченности магнетика(рис.7.1), из которой изготовлентрубчатыйпроводник,на внутреннейJ_{|r = R} сr = R радиусом и внешнейJ_{|r = 3R/2} сr = 3R/2 радиусомповерхностяхтрубчатогопроводника с учётом(1.9) имеет следующий вид: J_{l|r = R} = 0 А/м; J_{l|r = 3R/2} = 0 А/м. (1.10) На внутреннейи внешнейповерхностяхтрубчатогопроводника согласно(1.9) проекция J _l(r) навектор dl обхода Г контура вектором J(r)намагниченностимагнетика(рис.7.1.1), из которой изготовлентрубчатыйпроводник, равна нулю, а между этими поверхностями, т.е. при R ≤ r ≤ 3R/2, согласно (1.9) эта проекция J _l(r магнетика отлична от нуля, т.е. магнетикявляется парамагнитным, ферромагнитным илидиамагнитнымматериалом. Поэтому вектор J(r) намагниченностимагнетика, из которой изготовлентрубчатыйпроводник, совпадает по направлению (рис.7.1) с векторами H(r), B(r) соответственно индукцииинапряжённостимагнитного поля в случаепарамагнитного, ферромагнитного магнетикасмагнитной χ > 0 восприимчивостью магнетика, из которого изготовлентрубчатыйпроводник; в случае диамагнитногомагнетика с χ < 0 восприимчивостью вектор J(r) намагниченностимагнетика противоположен по направлению с векторами H(r), B(r) соответственно индукцииинапряжённостимагнитного поля

Вектор J(r) намагниченностимагнетика(рис.7.1) коллинеарен орту e_φ цилиндрической системыкоординат, поэтому векторное выражение (1.9) имеет следующий вид: J(r) ={j[(27R³ - 8 r³)(r² - R²)]/16R³ r}e_φ, (1.11) где (рис.7.1.1) R ≤ r ≤ 3R/2.

Ротация вектора J(r) намагниченности (1.11) магнетикас учётом равенства нулю проекцийJ_r, J_Z этоговектора на соответственно e_r, e_Z орты в цилиндрической системекоординат и отличия от нуляпроекцииJ_φ на e_φ орт, а также с учётом зависимости этой проекции J_φ (1.11)только от r модуля r радиуса-вектора, направленного по орту e_r, приводит к следующему выражению вектора

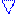
j_мол плотности молекулярных токов (7.116) из раздела 7.2 "Магнитное поле в веществе", равным значениюротора намагниченности [J] в произвольной точке пространства, зависящей в цилиндрической системекоординат только от r модуля r радиуса-вектора: j_мол = [ J] ={(1/r)[∂(rJ_φ)/∂r]}e_Z = j(1/R³)(54R³ - 40r³ + 24R²r)e_Z,(1.12) где (рис.7.1.1) R ≤ r ≤ 3R/2.

Проекция j_молZ наe_Z орт в цилиндрической системекоординат (рис. 7.1) вектора

j_молплотностимолекулярных токов на внутреннейи внешнейповерхностяхj_{молZ |r = R} сr = R;

j_{молZ |r = 3R/2} с r = 3R/2 срадиусамитрубчатогопроводника с учётом(1.12) имеет следующий вид: j_{молZ |r = R} = 38j А/м² ; j_{молZ |r = 3R/2} = -45j А/м². (1.13)

Качественный график (рис.7.2) модуля H(r) вектора H(r) напряжённостимагнитного поля в функции от rрадиусаокружности, охватывающейкольцевуюповерхность магнетика с внутреннимR радиусом и внешнимr радиусом, построенный с учётом (1.3) H(r) = 0, 5j[r- (R²/r)] А/м примерноимеет вид прямой, с равенствами этого модуля H(r) вектора H(r) напряжённостимагнитного поля на внутреннейH_{|r = R} = 0 А/м сr = R радиусом и внешнейH_{|r = 3R/2} = j(5/12)R А/м сr = 3R/2 радиусомповерхностяхтрубчатогопроводника из магнетика.

Качественный график (рис.7.2) модуля B(r) вектора B(r)индукции магнитного поля в функции от r радиусаокружности, охватывающейкольцевуюповерхность магнетика с внутреннимR радиусом и внешнимr радиусом, построенный (1.6) с учётом B(r) ≈ jμ₀0, 5j[2, 2r - 0, 5(r⁴/R³) - 2, 2R²/r + 0, 5(r²/R )] кг/с²А(Тл),имеет вид кривой, с равенствами этого модуля B(r) вектора B(r)индукции магнитного поля на внутреннейB| _{r = R} = 0 сr = R радиусом и внешнейB| _{r = 3R/2} = jμ₀(5/12)R кг/с²А(Тл) сr = 3R/2 радиусомповерхностяхтрубчатогопроводника из магнетика.

Согласно (1.12), (1.13) вектор j_мол плотности молекулярных токов на внутреннейповерхноститрубчатогопроводникаколлинеарен e_Z орту в цилиндрическойсистемекоординат и направлен с ним в одну сторону, а на внешней поверхности трубчатогопроводника вектор j_мол плотности молекулярных токов направлен в противоположную этому e_Z ортусторону. При значении модуля r₀ радиуса-вектора r₀, которое можно определить, приравняв (1.12) нулю, и которое находится в интервале R ≤ r ≤ 3R/2,векторj_мол0плотность молекулярных токов становится равной нулю. На окружности трубчатогопроводника (рис.7.2) с модулем r₀ радиуса-вектора r₀ происходит смена знака у вектора j_мол плотности молекулярных токов:

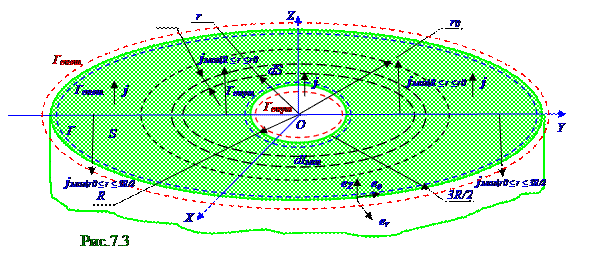
в интервале R ≤ r ≤ r₀ значений вектор плотности j_{мол|R ≤ r ≤ r0} молекулярных токов трубчатогопроводникаколлинеарен e_Z орту в цилиндрическойсистемекоординат и направлен с ним в одну сторону, а в интервале r₀ ≤ r ≤ 3R/2 значений вектор плотности j_{мол|r0 ≤ r ≤ 3R/2} молекулярных токов трубчатого проводника направлен в противоположную сторону этому e_Z орту.

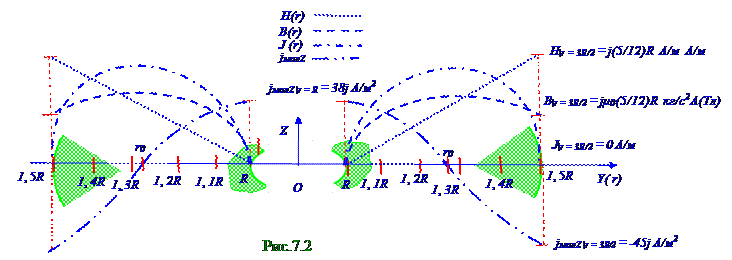
МолекулярныйdI_мол (7.108) из раздела 7.2 "Магнитное поле в веществе" ток, текущий через кольцо с элементарной(рис.7.3) толщиной dr и r радиусом, который находится в интервале R ≤ r ≤ 3R/2 значений, с учётом (1.13) имеет следующий вид:

dI_мол = j_молZ 2πrdr = j(2π/R³)(54R³r - 40r⁴ + 24R²r²) dr, (1.14)

где dS = 2πrdr - площадь элементарногокольца, перпендикулярнокоторому течёт молекулярныйdI_мол ток. МолекулярныйI_молток, текущий через поперечное сечение трубчатого проводника, представляющего собой кольцос внутреннимR радиусом и внешним3R/2 радиусом с учётом (1.14) имеет следующий вид:

3R/2 3R/2 3R/2

I_мол = ∫j_молdS= ∫ dI_мол = ∫j_мол2πrdr = j(2π/R³) ∫(54R³r - 40r⁴ +24R²r²) dr = 0 А.(1.15)

S R R R

МолекулярныйI_мол (1.12) ток с вектором j_мол плотности, текущий через поперечное сечение трубчатого проводника S площадью, согласно (7.108) из раздела 7.2 "Магнитное поле в веществе" по расчётам (1.15) имеет следующий вид: I_мол = ∫j_молdS = 0 А.(1.16) S

Проекция j_{мол.пов внутZ} на e_Z орт вектора j_{мол.пов внут} плотности поверхностноготока,которыйтечётв цилиндрической системе координатпо или противоположнонаправлениюe_Z орта по внутреннейповерхноститрубчатогопроводника, определяется (7.155) из раздела 7.2 "Магнитное поле в веществе" согласно следующему выражению: j_{мол.пов внут Z} = J_Гвнутl - J_Гвнутl = 0,(1.17)

где J_Гвнутl - проекция (рис.7.1) навектор dl обхода Г_внут воображаемого контура вектора J_Гвнутнамагниченности, который представляетсобойокружность R радиусом в материале трубчатого проводника; эта J_Гвнутl проекция согласно(1.10) равна нулю, т.е. J_Гвнутl = 0: J_Гвнутl - проекция навектор dl обхода Г_внут воображаемого контура вектора J(r)намагниченности, который представляетсобойокружность R радиусом в вакууме внутри трубчатого проводника, поэтому она тоже равна нулю, т.е. J_Гвнутl = 0.

Молекулярный I_{мол.пов внут}поверхностныйток (рис.7.1.3) на внутреннейповерхности трубчатогопроводника с учётом(1.17) имеет следующий вид: I_{мол.пов внут}= j_{мол.пов внутZ}2πR = 0,(1.18) где 2πR - длина контура c внутреннейстороны поперечного сечения материала трубчатого проводника, перпендикулярное его оси,вследствие чего длина этого контура R радиусом равна 2πR длине окружности.

где I_мол - молекулярныйток силой, текущий через поперечное сечение трубчатого проводника, представляющий собой кольцос внутреннимR радиусом и внешним3R/2 радиусом иравный (1.16) нулю, т.е. I_мол = 0; I_{мол.пов внут}-молекулярный поверхностныйток на внутреннейповерхности трубчатогопроводника, равный (1.18) нулю, т.е. I_{мол.пов внут} = 0.Поэтому молекулярныйрезультирующий ток I_{мол рез} силой,которыйохватывается Г_внеш воображаемымконтуром в виде окружностиr = 3R/2радиусом и который расположен внутри материала трубчатого проводника на его внешнейповерхности равен нулю, т.е. I_{мол рез}= 0.

Циркуляция (7.155) из раздела 7.2 "Магнитное поле в веществе" вектора J_Гвнешнамагниченности магнетика повоображаемой окружности(рис.7. 3) Г_внеш контуру в виде окружностиr = 3R/2радиусом c внутреннейстороны поперечного сечения трубчатогопроводникаиз магнетика c (1.1) μ(r) магнитной проницаемостью, перпендикулярного его оси, имеет с учётом (1.10) следующий вид: ∫J_Гвнеш dl= = J_{Гвнеш l}3Rπ = 0,(1.20) Г_внеш

где J_{Гвнеш l =} 0 -проекция навектор dl обхода Г_внеш контура (рис.7.1) вектора J_{Гвнеш l} намагниченности втрубчатомпроводникеиз магнетика с (1.1) μ(r) магнитной проницаемостью, который охватываетc внутреннейстороны поперечное сечение трубчатогопроводника, перпендикулярное его оси,вследствие чего длина этого Г_внеш контура 3R/2 радиусом равна 3πR длине окружности.

Молекулярныйрезультирующий ток I_{мол рез} |_Гвнеш силой,которыйохватывается Г_внеш воображаемымконтуром в виде окружности(рис.7.3) 3R/2радиусом и который расположен внутри материала трубчатого проводника на его внешнейповерхности равен (1.19) нулю, т.е. I_{мол рез} |_Гвнеш = 0.

Циркуляция вектора J_Гвнешнамагниченности магнетика повоображаемой окружности(рис.7. 1.3) Г_внеш контуру в виде окружности3R/2радиусомвнутри материала трубчатого проводника на его внешнейповерхности должна быть равна, согласно(7.155) из раздела 7.2 "Магнитное поле в веществе", молекулярномурезультирующему току I_{мол рез} |_Гвнеш силой,которыйохватываетсяэтим Г_внеш воображаемымконтуром.

Согласно(1.119) и (7.120) имеет место следующее равенство: ∫J_Гвнеш dl= I_{мол рез} |_Гвнеш,(1.21) Г_внеш что является подтверждением правильности расчётов в данной задаче.

Проекция j_{мол.пов внешZ} на e_Z орт вектора j_{мол.пов внеш} плотности поверхностноготока_.,которыйтечётв цилиндрической системе координатпо или противоположнонаправлениюe_Z орта по внешнейповерхноститрубчатогопроводника, определяется (7.155) из раздела 7.2 "Магнитное поле в веществе" согласно следующему выражению: j_{мол.пов внеш Z} = J_Гвнешl - J_{Гвнеш l} = 0,(1.22)

где J_внешl - проекция (рис.7.1) навектор dl обхода Г_внеш воображаемого контура вектора J_Гвнешнамагниченности, который представляетсобойокружность 3R/2радиусом снаружи внешнейповерхности трубчатого проводника; эта J_Гвнешl проекция равна нулю, потому что Г_внеш воображаемый контур находится в вакууме, т.е. J_Гвнешl = 0: J_Гвнешl - проекция навектор dl обхода Г_внеш воображаемого контура вектора J_Гвнешнамагниченности, который представляетсобойокружность 3R/2 радиусом внутри внешнейповерхноститрубчатого проводника, т.е. в материале магнетика; эта J_Гвнешl проекция согласно (1.10) равна нулю, т.е. J_Гвнешl = 0.

Молекулярный I_{мол.пов внеш}поверхностныйток (рис.7.1.3) на внешнейповерхности трубчатогопроводника с учётом(1.22) имеет следующий вид: I_{мол.пов внеш}= j_{мол.пов внеш Z}3πR = 0,(1.23) где 3πR - длина контура c внешнейстороны поперечного сечения материала трубчатого проводника, перпендикулярное его оси,вследствие чего длина этого контура 3R/2 радиусом равна 3πR длине окружности.

Задача 7.1.2

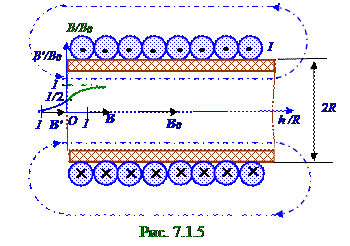
Длинный соленоид в вакууме имеет R радиус сечения и n витков на единицу длины. По нему течёт постоянный ток I силой. Найти B', B модуливекторов индукции магнитного поля на оси в функции h расстояния от торца соответственно B'вне и B внутриэтого соленоида. Изобразить примерный график зависимости B модулявектора B индукции магнитного поля на оси в функции

h расстояния от торца вне и внутрисоленоида, отнесённого к R радиусу этого соленоида, т.е. в зависимости от h/R.Дано: R; n; I/ B(h) = ? График B(h/R) = ?

Линейнаяj_линплотностьтока (7.31) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" вдлинном соленоидеимеет следующий вид: j_лин = nI. (2.1)

Ток dI силой в витках соленоида, которые (рис. 7.4 а, б) расположены на элементарной

dy длине имеет следующий вид: dI = nIdy. (2.2) Проекция dB'_{M' Y} на OY ось вектораdB'_M'магнитной индукции в M ' точкевне соленоида, находящейся на осиэтого соленоида с h расстояниемот его торца, от витков соленоида, которые

(рис.7.4 а) расположены на элементарнойdy длине имеет (7.15) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" с учётом (2.2) следующий вид: dB'_{M' Y} = dB'_M' = μ₀dIR²/2[R² + (y + h)²] ^3/2 = μ₀nIR²dy/2[R² + (y + h)²] ^3/2, (2.3)

где dB'_{M' Y} = dB'_M' - проекцияна OY ось вектораdB'_M'магнитной индукции в M' точкевне соленоида равна, вследствие направления этоговектораdB'_M' по OY оси, dB'_M' модулювектораdB'_M'магнитной индукции в M' точкевне соленоида; (y + h) - расстояние (7.15) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" от витков соленоида, которые (рис.7.4 а) расположены на элементарнойdy длине и имеют y координату M' точкивне соленоида.

Проекция B'_{M' Y} на OY ось вектора B'_M'магнитной индукции в M ' точкевне соленоида, находящейся на осиэтого соленоида с h расстояниемот его торца, от всех витков соленоида, которые

(рис. 7.4 а) расположены на длине от 0 до ∞ координат по OY оси имеет с учётом (2.3) следующий вид: ∞

B'_{M' Y} = B'_M' = μ₀nIR²∫ dy/2[R² + (y + h)²] ^3/2 = (μ₀nI/2){1 - [h/(R² + h²)^1/2]} ↔

0

↔ B'_M' =(B₀/2){1 - [(h/R) /(1 + h²/R ²) ^1/2]}, (2.4)

где B'_{M' Y} = B'_M' - проекция B'_{M' Y} на OY ось вектора B'_M'магнитной индукции в M' точкевне соленоида равна, вследствие направления этоговектора B'_M' по OY оси, B'_M' модулювектора B'_M'магнитной индукции в M' точкевне соленоида, находящейся на осисоленоида с h расстояниемот его торца;

B₀ = μ₀nI - модуль вектораB₀ индукциимагнитного поля (7.34) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" в середине(рис.7.8) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" длинного соленоида, находящегося ввакууме.

Согласно (2.4) приh/R= 0, т.е. при нахождении M' точки на торце соленоида, B'_M' модульвектора B'_M'магнитной индукции равен B₀/2 = μ₀nI/2 половине модуля B₀ вектораB₀ индукциимагнитного поля в серединедлинного соленоида, находящегося ввакууме. Это отражено синей линией на примерном графике (рис. 7.5) зависимости B'/B₀ модуля, отнесённого кмодулю

B₀ вектораB₀ индукциимагнитного поля в серединедлинного соленоида,в функции h расстояния от торца вне соленоида, отнесённого к R радиусу этого соленоида, т.е. в зависимости от h/R. При h/R > 3, т.е. при нахождении M' точки по осина h > 3R расстоянии от торцавне соленоида B'_M' модульвектора B'_M'магнитной индукции не превышает величины 0, 03B₀, т.е. B'_M'| _{h/R > 3} < 0, 03B₀.

Проекция dB٭_MY на OY ось вектораdB٭_Mмагнитной индукции в M точкевнутрисоленоида, находящейся на осисоленоида с h расстояниемот его торца, от витков соленоида, которые

(рис. 7.4 б) расположены на элементарнойdy длине слеваот этой M точкивнутрисоленоида, имеет (7.15) из раздела 7.1 "Магнитостатика" с учётом (2.5) следующий вид:

dB٭_{M Y} = dB٭_M = μ₀dIR²/2[R² + (h - y)²] ^3/2 = μ₀nIR²dy/2[R² + (h - y)²] ^3/2, (2.5) где dB٭_{M Y} = dB٭_M - проекцияна OY ось вектораdB٭_Mмагнитной индукции в M точкевнутри соленоида равна, вследствие направления этоговектораdB٭_M по OY оси, dB٭_M модулювектораdB'_M'магнитной индукции в M точкевнутри соленоида; (h - y) - расстояние (7.15) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" от витков соленоида, которые (рис.7.4 а) расположены на элементарнойdy длине и имеют y координату слеваот этой M точкивнутрисоленоида.

Проекция B٭_MY на OY ось вектора B٭_Mмагнитной индукции в M точкевнутри соленоида, находящейся на осиэтого соленоида с h расстояниемот его торца, от всех витков соленоида, которые

(рис. 7.4 б) расположены слеваот этой M точкивнутрисоленоида на длине от 0 до h координат по OY оси имеет с учётом (2.2) следующий вид:

h

B٭_MY = B٭_M = μ₀nIR²∫dy/2[R² + (h - y)²] ^3/2 = (μ₀nI/2)[h/(R² + h²)^1/2], (2.6)

0

где B٭_MY = B٭_M - проекцияна OY ось вектора B٭_Mмагнитной индукции в M точкевнутри соленоида равна, вследствие направления этоговектора B٭_M по OY оси, B٭_M модулювектора B٭_Mмагнитной индукции в M точкевнутри соленоида, находящейся на осисоленоида с h расстояниемот его торца.

Проекция dB٭٭_MY на OY ось вектораdB٭٭_Mмагнитной индукции в M точкевнутрисоленоида, находящейся на осисоленоида с h расстояниемот его торца, от витков соленоида, которые

(рис. 7.4 б) расположены на элементарнойdy длине справаот этой M точкивнутрисоленоида, имеет (7.15) из раздела 7.1 "Магнитостатика" с учётом (2.2) следующий вид:

dB٭٭_{M Y} = dB٭٭_M = μ₀dIR²/2[R² + (y - h)²] ^3/2 = μ₀nIR²dy/2[R² + (y - h)²] ^3/2, (2.7) где dB٭٭_MY = dB٭٭_M - проекцияна OY ось вектораdB٭٭_Mмагнитной индукции в M точкевнутри соленоида равна, вследствие направления этоговектораdB٭٭_Mпо OY оси, dB٭٭_M модулювектораdB٭٭_Mмагнитной индукции в M точкевнутри соленоида; (y - h) - расстояние (7.15) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" от витков соленоида, которые (рис. 7.4 а) расположены на элементарной

dy длине и имеют y координату справаот этой M точкивнутрисоленоида.

Проекция B٭٭_MY на OY ось вектора B٭٭_M магнитной индукции в M точкевнутри соленоида, находящейся на осиэтого соленоида с h расстояниемот его торца, от всех витков соленоида, которые

(рис. 7.4 б) расположены справаот этой M точкивнутрисоленоида на длине от h до ∞ координат по OY оси имеет с учётом (2.7) следующий вид: ∞

B٭٭_MY = B٭٭_M = μ₀nIR²∫dy/2[R² + (y - h)²] ^3/2 = μ₀nI/2, (2.8)

h

где B٭٭_MY = B٭٭_M - проекцияна OY ось вектора B٭٭_M магнитной индукции в M точкевнутри соленоида равна, вследствие направления этоговектора B٭٭_M по OY оси, B٭٭_M модулювектора B٭٭_M магнитной индукции в M точкевнутри соленоида, находящейся на осисоленоида с h расстояниемот его торца.

РезультирующийB_M модульвектора B_M магнитной индукции в M точкевнутри соленоида от всех витков соленоида, которые (рис. 7.4 б) расположены слева и справа иот этой M точкивнутрисоленоида на длине от 0 до ∞ координат по OY оси имеет с учётом (2.6), (2.8) следующий вид:

B_M = B٭_M + B٭٭_M = (μ₀nI/2){1 + [h/(R² + h²) ^1/2]} ↔ B_M = (B₀/2){1 + [(h/R) /(1 + h²/R ²) ^1/2]}, (2.9)

где B₀ = μ₀nI - модуль вектораB₀ индукциимагнитного поля (7.34) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" в середине(рис.7.8) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" длинного соленоида, находящегося ввакууме.

Согласно (2.9) приh/R= 0, т.е. при нахождении M точки на торце соленоида, B_M модульвектора B_Mмагнитной индукции равен B₀/2 = μ₀nI/2 половине модуля B₀ вектораB₀ индукциимагнитного поля в серединедлинного соленоида, находящегося ввакууме. Это отражено зелёной

Задача 7.1.3

Вдоль длинного цилиндрического провода R радиуса, сделанного из однородного парамагнетика с магнитной χ восприимчивостью, течёт постоянный ток I силой. Определить модуль j_мол, направление вектора j_мол плотности молекулярного тока в зависимости от r расстояния до OO′ оси цилиндрического провода, а также определить поверхностный I_{мол.пов.} и объёмный I_мол. молекулярный ток в этом цилиндрическом проводе и их направление.Дано: χ; R; I/ j_мол = ? j_мол = ? I_мол. = ?I_{мол.пов} = ?

проводником из магнетикас магнитной χ восприимчивостью, и направленыпо касательнойк этой окружности, т.е. коллинеарны e_φ орту цилиндрической системыкоординат.

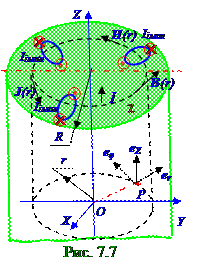
Циркуляция (7.124) из раздела 7.2 "Магнитное поле в веществе" вектора H(r)напряжённостимагнитного поля в интегральномвиде (рис. 7.7) повоображаемой окружностиr радиусом в области пространства, занятого магнетиком, равна (3.2)результирующему I_рез макроскопическому или току проводимости через поверхность S площадью, которую охватывает эта воображаемая окружность r радиусом.

Модуль H(r)вектора H(r) напряжённостимагнитного поля при циркуляции повоображаемой окружности(рис. 7.7) радиусом r постоянен, поэтому с учётом (3.2) модуль H(r) вектора H(r) напряжённостимагнитного поля в функции от радиуса rокружности, охватывающей круг

r радиусом, имеет следующий вид: H2πr = I_рез ↔ H2πr = r²I/R² ↔ H = rI/2πR²,(3.3) где (рис. 7.7) 0 ≤ r ≤ R.

НамагниченностьJ (7.126) из раздела 7.2 "Магнитное поле в веществе" магнетика, из которой изготовленцилиндрическийпроводник, имеет следующий вид: J = χH,(3.4)

где вектор J намагниченности сонаправлен вектору H напряжённостимагнитного поля (3.3)в магнетике цилиндрическогопроводника, когда χ > 0 для парамагнетикови ферромагнетиков, и вектор J намагниченности противонаправлен вектору H напряжённостимагнитного поля (3.3)в магнетике цилиндрическогопроводника, когда χ < 0 для диамагнетиков.

Подставляем магнитную χ восприимчивость магнетика, из которой изготовленцилиндрическийпроводник, а также (3.3) модуль H(r)вектора H(r)напряжённостимагнитного поля в (3.4), представленное в виде модулей, и получаем следующее выражение для J(r) намагниченности магнетика, из которой изготовленэтот цилиндрическийпроводник,в функции от r радиуса окружности, охватывающей круговуюповерхность магнетика: J(r) = χH(r) = χrI/2πR² А/м,(3.5) где (рис. 7.7) 0 ≤ r ≤ R.

НамагниченностьJ(r)на круговойповерхности магнетикаr = R радиусом с учётом(3.5) имеет следующий вид: J_{|r = R} = χI/2πR А/м. (3.6) Вектор J(r) намагниченностимагнетика(рис.7.7) коллинеарен орту e_φ цилиндрической системыкоординат, поэтому векторное выражение (3.5) имеет следующий вид: J = χH = e_φ χrI/2πR² А/м,(3.7)

где (рис.7.7) 0 ≤ r ≤ R.

Ротация вектора J(r) намагниченности (3.7) магнетикас учётом равенства нулю проекцийJ_r, J_Z этоговектора на соответственно e_r, e_Z орты в цилиндрической системекоординат и отличия от нуляпроекцииJ_φ на e_φ орт, а также с учётом зависимости этой проекции J_φ (3.7)только от r модуля

r радиуса-вектора, направленного по орту e_r, приводит к следующему выражению вектора

j_мол плотности молекулярных токов (7.116) из раздела 7.2 "Магнитное поле в веществе", равным значениюротора намагниченности [J] в произвольной точке пространства, зависящей в цилиндрической системекоординат только от r модуля r радиуса-вектора: j_мол = [ J] ={(1/r)[∂(rJ)/∂r]}e_Z =e_ZχI/πR²,(3.8) где (рис.7.7) 0 ≤ r ≤ R.

Вектор j_мол плотностимолекулярных токов направлен по OZ оси, поэтому проекция j_молZна

e_Z орт в цилиндрической системекоординат (рис. 7.7) положительна, является следующей постоянной величиной в пределах поперечного сечения кругаR радиусоммагнетика цилиндрическогопроводника:j_молZ = χI/πR²,(3.9)

где (рис.7.7) 0 ≤ r ≤ R.

Молекулярныйток dI_мол силой (7.108) из раздела 7.2 "Магнитное поле в веществе" ток, текущий через кольцо с элементарной(рис. 7.1.8) толщиной dr и r радиусом, который находится в интервале 0 ≤ r ≤ R значений, с учётом (3.9) имеет следующий вид:

dI_мол = j_мол2πrdr = (χI/πR²)2πrdr = χ2Irdr/R², (3.10)

где dS = 2πrdr - площадь элементарногокольца, перпендикулярнокоторому течёт молекулярныйток dI_мол силой.

МолекулярныйI_мол результирующийток, текущий (рис. 7.8) через поперечное сечение кругаR радиусоммагнетика цилиндрическогопроводника с учётом (3.10) , согласно (7.108) из раздела 7.2 "Магнитное поле в веществе", имеет следующий вид:

R R I_мол = ∫j_молdS= ∫ dI_мол = (χ2I/R²) ∫rdr = χI А, (3.11)

S 0 0

где молекулярныйI_мол результирующийток направлен по OZ оси, т.е. в одну сторону срезультирующейсилой I_рез тока проводимости в магнетике цилиндрическогопроводника, если χ>0 для парамагнетикови ферромагнетиков, а, если χ < 0 для диамагнетиков, то молекулярныйI_мол результирующийтокнаправлен противоположно OZ оси, т.е. в противоположную сторону срезультирующейсилой I_рез тока проводимости в магнетике цилиндрическогопроводника.

проводника, если χ>0 для парамагнетикови ферромагнетиков, а, если χ < 0 для диамагнетиков, то молекулярныйI_мол результирующийтокнаправлен противоположно OZ оси, т.е. в противоположную сторону срезультирующейсилой I_рез тока проводимости в магнетике цилиндрическогопроводника.

Равенство(3.11) и (3.12) соответствует следующему (7.115) из раздела 7.2 "Магнитное поле в веществе" : I_мол = ∫j_молdS = ∫Jdl, (3.13)

S Г

что является подтверждением правильности расчётов в данном выводе.

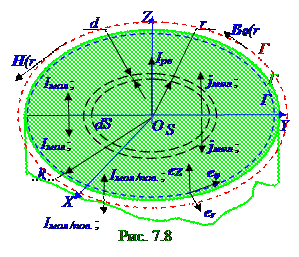
Циркуляция (7.115) из раздела 7.2 "Магнитное поле в веществе" вектора J(r) намагниченности (3.7) магнетикамагнитного поля в интегральномвиде повоображаемой окружности -(рис. 7.8) Г контуру R радиусом c внешнейстороны боковой поверхности цилиндрическогопроводникаиз магнетика равнаследующей сумме молекулярныхтоков I_мол;I_{мол.пов.}силой,соответственно текущих через поверхность S площадью и по боковой поверхности цилиндрическогопроводникаиз магнетика:

∫Jdl =I_мол +I_{мол.пов} = 0 ↔ I_мол = -I_{мол.пов}, (3.14)

Г

где (3.14) приравнено нулю, п.ч. Г контур R радиусом cвнешнейстороны боковой поверхности цилиндрического проводникаиз магнетикапроходит в вакууме,где векторJ(r) намагниченностиравен нулю.

Согласно (3.14)молекулярныетоки I_мол;I_{мол.пов.}силой,соответственно текущие через поверхность S площадью и по боковой поверхности цилиндрическогопроводникаиз магнетика,компенсируютдруг друга, поскольку текут навстречу, а их величины равны друг другу.

Задача 7.1.4

Постоянный кольцевой магнит со средним R радиусом имеет в вакууме поперечный зазор

b шириной.Модуль вектора Bиндукции магнитного поля в зазоре между полюсами этого магнита равен B. Считая, что рассеяния магнитного поля на краях зазора нет, найти H модуль и направление вектора Hнапряжённости магнитного поля в материале кольцевого магнита. Дано:R; b; B / H = ? H = ?

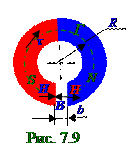
Проекция H_τ на касательный τ ортквоображаемой окружностиR радиусом, т.е.Г контуру,в области пространства, занятого материалом магнита и в зазоре между полюсами этого магнита, вектора Hнапряжённостимагнитного пол