Исследование поляризационных свойств стеклянной призмы

Цель работы – овладеть техникой проведения визуальных поляризационных измерений с применением кристаллической пластины. Исследовать поляризующую способность призмы Дове и проверить соответствие полученных экспериментальных данных расчитанным по формуле Френеля.

Призма Дове (рис. 1) применяется в оптических приборах для поворота изображения предметов.

i₁ N

40º i₂ n = 1.52

Рис. 1. Схема лучей в призме Дове

Лучи, проходящие через призму, испытывает преломление на входной и выходной гранях и полное внутреннее отражение на нижней грани. Анизотропия процессов преломления и отражения приводят к поляризации проходящего света [1–a]. Поэтому при работе призмы в естественном свете (неполяризованном и некогерентном) проходящий свет становится частично поляризованным. В случае работы в поляризованном свете имеют место интерференционные явления, приводящие к изменению состояния поляризации. В зависимости от азимута 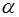плоскости поляризации падающего линейно - поляризованного света выходящий свет может стать эллиптически поляризованным, или остаться линейно поляризованным.

Рассмотрим процессы, приводящие к поляризации призмой исследуемого света. Будем считать, что плоскость падения лучей на призму вертикальна. Известно, что свет с любым видом поляризации можно представить в виде двух составляющих с ортогональными преимущественными колебаниями электрических векторов. Поляризацию с колебаниями электрического вектора в плоскости падения будем называть параллельной, или р – поляризацией, а вторую, с перпендикулярными колебаниями, перпендикулярными, или s –поляризацией. Обозначим через T_1p и T_1s соответствующие составляющие энергетических коэффициентов пропускания на первой грани.

Из формул Френеля следует :

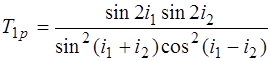
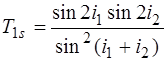(1)

где i₁ ­– угол падения, i₂ – угол преломления.

Очевидно, что на второй преломляющей грани коэффициенты T_2p = T_1p и T_2s = T_1s , а суммарное пропускание T_p = T_1pT_2p = 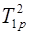и .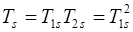

В результате неравенства T_p и T_s прошедший свет становится частично поляризованным. Степень его поляризации:

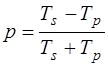(2)

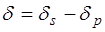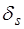В случае прохождения поляризованного, когерентного света p и s – составляющие могут взаимодействовать. При полном внутреннем отражении между колебаниями в этих составляющих возникает разность фаз , где и 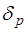– соответствующие сдвиги по фазе. Величина 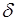зависит от угла падения 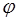и величины 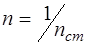, где – показатель преломления стекла:

(3)

Сложение ортогонально ориентированных колебаний с разностью фаз 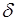приводит в общем случае к появлению эллиптически поляризованного света. Пространственная ориентация эллипса и его эллиптичность зависят от азимута 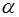(отсчитываемого от плоскости падения). При 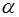, равном нулю или 90°, свет остаётся линейно поляризованным [2].

Анализ состояния поляризации эллиптически поляризованного света осуществляется с помощью поляризационных компенсаторов. В настоящей работе используется компенсатор Сенармона [1 – б]. Он представляет собой сочетание кристаллической пластинки, вырезанной параллельно оптической оси и вносящей разность фаз p/2, и анализатора (поляризатора), расположенных последовательно. Пластинка 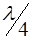при определенной своей ориентации превращает исследуемый эллиптический свет в линейно поляризованный. Азимут полученного линейно поляризованного света определяется с помощью анализатора.

Рассмотрим физическую сторону процесса исследования поляризующей способности призмы Дове, имея в виду измерение вносимых ею разности фаз 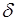и поворота плоскости поляризации . Предположим, что плоскость поляризации света, падающего на первую грань призмы, выставлена под углом 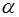по отношению к плоскости падения света (рис. 2).

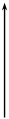p B y s'

p'

E_p Е₀ a = 45°

b

O s

E_s

а

Рис. 2. Поляризационный эллипс и его параметры

Пусть 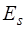и 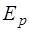– ортогональные проекции электрического вектора 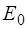падающей волны с амплитудо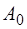й . При 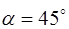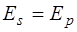. В этом случае при произвольном значении 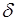, вводимым между этими компонентами, выражение для эллипса поляризации имеет вид:

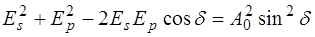, (4)

а его большая ось располагается под углом 45° к плоскости падения света. Уравнение этого эллипса в системе координат 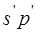, повернутой на 45° и совпадающей с его осями, приобретает каноническую форму:

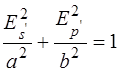, (5)

где а и b – величины полуосей эллипса. При этом

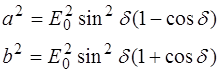
Вычислив отношение полуосей b/a, получаем, что

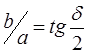(6)

Таким образом, для определения величины 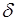необходимо измерить отношение b/a.

В методе Сенармона это измерение основывается на следующем обстоятельстве. Известно, что эллипс по (5) образуется в результате сложения двух взаимно перпендикулярных колебаний вдоль осей эллипса, имеющих амплитуды а и b и разность фаз p/2. Следовательно, вводя в ход лучей компенсационную пластинку 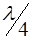с и поворачивая ее так, чтобы ее главные направления совпали с осями эллипса поляризации, мы получим после нее линейно поляризованный свет, так как выходящие колебания будут синфазными (разность фаз между взаимно перпендикулярными колебаниями равна нулю). Компоненты а и b сложатся по правилу векторного сложения и получится результирующее колебание с вектором ОВ (рис. 2).

E_p p

E₀

E_p

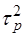
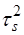E_s E_s s

Рис. 3. p – и s – компоненты вектора Е₀

Если первоначально анализатор был установлен в скрещенное положение с поляризатором, то теперь поле просветлится. Поворачивая анализатор на угол 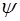, можно опять добиться темноты поля. Очевидно, что . (7)

Из выражений (6) и (7) следует, что

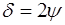(8)

Процесс измерения величины 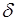в случае призмы Дове осложняется тем обстоятельством, что коэффициенты пропускания для s и р – компонент различны.

Учитывая амплитудные коэффициенты пропускания на каждой преломляющей грани

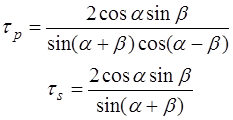(9)

и, обращаясь к рис. 3, видим, что призма поворачивает плоскость поляризации света. В результате этого поворачивается и эллипс поляризации. Поэтому при повороте анализатора не наступает полное гашение, а соотношение (8) не выполняется точно. Для получения правильного результата нужно установить угол α', при котором ортогональные составляющие будут равны, т.е.

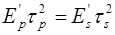
Отсюда следует

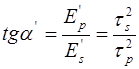и с учетом (9) получаем

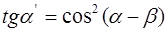(10)

Угол поворота плоскости поляризации

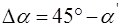(11)

В реальном эксперименте, как будет указано ниже, этот угол устанавливается путем малых приближений.

Задание

1. Научиться выставлять плоскости поляризации поляризатора и анализатора вертикально и горизонтально (параллельно и перпендикулярно плоскости падения света на призму Дове).

2. Исследовать зависимость вида эллипса поляризации света, прошедшего пластинку 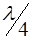, от азимута поляризации при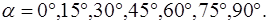

3. Исследовать зависимость вида эллипса поляризации света, прошедшего призму Дове, от азимута поляризации при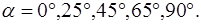

4. Пользуясь методом Сенармона, измерить разность фаз, возникающую при полном внутреннем отражении в призме. Оценить вносимый призмой поворот плоскости поляризации.

5. Рассчитать степень поляризации в прошедшем призму свете при ее освещении естественным светом.

6. Рассчитать разность фаз при полном внутреннем отражении в призме, вносимый ею поворот плоскости поляризации и сопоставить их с экспериментальными данными.