Поляризация диэлектриков в электростатическом поле. Свободные, поляризационные заряды в диэлектрике 4 страница

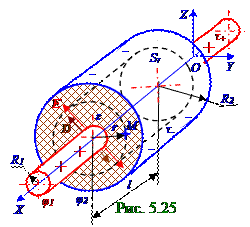
ε - относительнаядиэлектрическаяпроницаемость диэлектрикамежду внутренними внешнимцилиндрами.

Интегрирование (5.126) с использованием (5.117) от внутреннегоцилиндра R₁радиусом

(рис. 5.25) довнешнегоцилиндра R₂ радиусом приводит к следующему выражению φ₁ - φ₂ разности потенциалов между этими цилиндрами:R₂ R₂

φ₁ - φ₂ = ∫ E_rdr= (τ/2πεε₀)∫dr/r = τln(R₂/R₁)/2πεε₀ = qln(R₂/R₁)/2πεε₀l, (5.127)

R₁ R₁

где τ = q/l - линейная плотность зарядов(рис.5.24) на внутреннемцилиндре R₁ радиусом, постоянная на всей длине l конденсатора; q - заряд навнутреннемцилиндре l длиной.Из выражения (5.127) ёмкостьCкоаксиального конденсатораc lдлиной цилиндрических обкладокR₁, R₂ радиусамии диэлектрикомс ε относительной диэлектрическойпроницаемостьюмежду ними имеет следующий вид: C = q/(φ₁ - φ₂) = 2πε₀εl/ln(R₂/R₁). (5.128)

Емкость сферического конденсатора

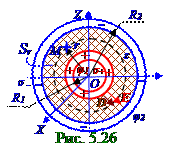
напряжённости электростатическогополя в произвольной M точке пространствадиэлектрической среды между внутреннейи внешнейсферами c учётом одинаковойструктуры электростатическогополя в случае (рис.5.26) сферического конденсатора и (рис.5.22, а) уединённой проводящей сферической поверхности имеет согласно (5.118) следующий вид: E_r = D_r/ε₀ε = q/4πε₀εr², (5.129) где R₁ ≤ r ≤ R₂ - длина r радиус - вектораот центра внутреннейсферы до произвольной M точки в зазоре между внутреннейи внешнейсферами; D_r - проекция на направление r радиуса - вектора

D вектораэлектрического смещения в произвольной M точке пространствадиэлектрической среды между внутреннейи внешнейсферами; ε - относительная проницаемостьдиэлектрической среды между внутреннейи внешнейсферами; q -свободный заряд внутреннейсферы, который охватываетсяпо теореме (5.20) Остроградского - Гаусса замкнутой воображаемойсферической поверхностью S_r площадью, равной 4πr², т.е. S_r = 4πr², на которой находится произвольная M точка пространствадиэлектрической среды.

Интегрирование (5.129) с использованием (5.117) от внутренней сферы R₁радиусом

(рис.5.26) довнешней сферы R₂ радиусом приводит к следующему выражению φ₁ - φ₂ разности потенциаловмежду ними: R₂ R₂

φ₁ - φ₂ = ∫ E_rdr= (q/4πε₀ε) ∫dr/r² = (q/4πε₀ε)[(1/R₁) - (1/R₂)].(5.130) R₁ R₁

Из выражения ((5.125) ёмкостьCсферического конденсатораc обкладкамиR₁, R₂ радиусови диэлектрикомс ε относительной диэлектрическойпроницаемостьюмежду ними имеет следующий вид: C = q/(φ₁ - φ₂) = 4πε₀ε(R₁R₂)/(R₂ - R₁). (5.131)

Энергия взаимодействия системы точечных зарядов

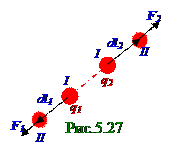
Элементарная δAработа, совершаемая силами (5.43) потенциального электростатическогополя, т.е.(5.1) консервативнымисиламиКулона,при (рис.5.27) перемещении, например, положительныхq₁ и q₂ зарядов в направлении векторов F₁, F₂ этих силКулонана dl₁, dl₂ элементарные векторы, равна согласно (1.95) из раздела 1 "Физические основы механики" элементарному приращениюdW_pпотенциальной энергии как дифференциалу функции, т.е. следующей разности потенциальной энергииW_pII во II состоянии и W_pI в I состоянии q₁ и q₂ зарядов, взятого со знаком "-": δA = - (W_pII - W_pI ) = - dW_p = - dW_вз , (5.132)

где dW_вз - элементарное приращение потенциальнойэнергии взаимодействия q₁ и q₂ зарядов при

W_вз = (1/2)[(W₁₂ + W₁₃) + (W₂₁ + W₂₃) + (W₃₁ + W₃₂)],(5.134) где W₁₂ и W₁₃ - энергия взаимодействия 1-го q₁ заряда со 2 -ым q₂ и3 -им q₃ зарядами; W₂₁ и W₂₃ - энергия взаимодействия 2-го q₂ заряда со 1 -ым q₁ и 3 -им q₃ зарядами; W₃₁ и W₃₂ - энергия взаимодействия 3-го q₃ заряда со 1 - ым q₁ и 2 - ым q₃ зарядами.

В общем случае при наличии q₁, q₂, …, q_nзарядов согласно (5.50), если точечнымпробным q_пр зарядом считать поочерёдно каждый из n - зарядов q_i с индексом i, находящийся в электростатическомполеокружающих

W_вз = (1/2)[(W₁₂ + W₁₃ +… +W_1n) + (W₂₁ + W₂₃+… +W_2n) +…+ (W _n1 + W _n3+… +W _{n (n-1)} )] =

n n n-1 n n n-1 n n

= (1/2)(∑W_1j + ∑W_2j + … + ∑W_nj) = (1/2)( q₁∑φ_j + q₂∑φ_j + … + q_n∑φ_j) = (1/2) ∑q_i∑φ_j.(5.135)

j=2 j=1 j=1 j=2 j=1 j=1 i=1 j=1

j≠1 j≠2 j≠n j≠1 j≠2 j≠n j≠i

где при суммировании φ_j потенциалов электростатическогополя, создаваемых в точке нахождения q_i заряда всеми остальными (n -1) - зарядами индекс j = i исключается, т.е. j ≠ i.

Если q₁, q₂, …, q_nзаряды находятся в линейном изотропном диэлектрике с εдиэлектрическойпроницаемостью этого диэлектрика, то φ_jпотенциал электростатическогополя от j - го точечного заряда в точке расположения q_i заряда определяется (5.113) следующим выражением: φ_j = q_j/4πε₀εr_{i j}, (5.136)

где r_{i j} - расстояние между q_i зарядом, в точке расположения которого определяется φ_jпотенциал, и q_j зарядом, от электростатическогополя которого в точке расположения этого q_i заряда потенциал равен φ_j.

Подставим (5.136) в (5.135) и получим следующее выражение для энергии W_вз взаимодействия n - зарядов, находящихся в линейном изотропном диэлектрике с ε диэлектрическойпроницаемостью: n n n

W_вз = (1/8πε₀ε)∑q_i ∑ q_j/r_{i j} = (1/2)∑q_iφ_i, (5.137)

i=1 j=1 i=1 n j≠i

где (1/4πε₀ε)∑ q_j/r_{i j} = φ_i- это потенциал,создаваемый в точке нахождения q_i заряда

j=1

j≠i

всеми (n -1) - зарядами, окружающих этот q_i заряд. В этом φ_i потенциале не учитывается

φ_сi собственный потенциал, создаваемый самим q_i зарядом в точке пространства, где находится этот

q_i заряд, когда вокруг q_i заряда отсутствуют окружающие (n -1) - заряды.

Собственная энергия заряженных проводников

Элементарная работа δA′ внешнихсил при перемещении dqэлементарногозаряда из бесконечностис φ₁ = 0 потенциалом на проводник с φ потенциалом равна δA элементарной работе, совершаемой силами электростатическогополя, взятой с противоположнымзнаком, и с учётом (5.51) имеет следующий вид: δA′ = - δA = - dq(φ₁ - φ) = φdq.(5.138)Дифференциалdq заряда с учётом(5.116) постоянного значения C ёмкости имеет следующий вид: dq = Cdφ. (5.139) Подставим (5.139) в (5.138) и получим следующее выражение для δA′ элементарной работы внешнихсил по перемещению dqэлементарногозаряда из бесконечностис φ₁ = 0 потенциаломна проводник с φ потенциалом: δA′ = Cφdφ. (5.140) Согласно (5.140) элементарная δA′ работа, выполненная внешнимисилами по перемещению dqэлементарногозаряда из бесконечностина проводник с φ потенциалом, пропорциональна dφэлементарномуприращению потенциалу этого проводника. Отсюда A_i′ работа, выполняемая внешнимисилами, для увеличения потенциалаi -го проводника до произвольного значения φ_i имеет следующий вид: φ_i A_i′ = ∫Cφdφ = Cφ_i²/2. (5.141) 0 РаботаA_i′ внешнихсил из (5.141) увеличила W_сiсобственнуюэнергию i -го проводника от 0 до величины, определяемую его φ_i потенциалом. С учётом (5.116) определения C_i электроёмкости i -го проводника W_сi собственная энергия этого i -го проводника принимает следующий вид: W_сi = C_iφ_сi²/2 = q_i²/2C_i = q_iφ_сi/2, (5.142) где q_i, φ_сi, C_i - соответственно заряд, собственный потенциали ёмкость уединённогоi -го проводника, т.е. когда окружающие этот i -ый проводник остальные (n -1) - проводников отсутствуют.

Собственная W_с энергия всех n-проводниковс q_i зарядами и φ_сi собственными потенциаламиопределяетсясуммированием(5.133)собственных W_сi энергий i -ых проводников, вследствие чего для определения собственной W_с энергия всех n-проводниковс q_i зарядами имеет место следующее выражение: n

W_с = (1/2)∑q_iφ_сi, (5.143)

i=1

Полная энергия заряженных проводников

Полная W энергия всех n -проводниковсучётом (5.143) собственных W_с энергий всех n-проводниковиэнергии (5.135) W_вз взаимодействия этих n-проводников, находящихся в линейном изотропном диэлектрике с ε относительной диэлектрическойпроницаемостью или вакууме, имеет следующий вид: n n

W = W_с + W_вз = (1/2)∑q_iφ_сi + (1/2)∑q_iφ_i, (5.144)

i=1 i=1

где (5.116) φ_сi - собственный потенциал уединённогоi -го проводника с q_i зарядом, т.е. когда окружающие этот i -ый проводник остальные (n -1) - проводники отсутствуют; φ_i (5.137) - потенциал, создаваемый всеми (n -1) -проводниками с q₁, q₂,…, q_{(n -1)} зарядами, окружающими i -ый проводник с q_i зарядом в точке пространства, где располагается этот i -ый проводник с q_i зарядом. В этом φ_iпотенциале не учитывается собственныйφ_сi потенциал, создаваемый самим i -ым проводником с q_i зарядом в точке пространства, где находится этот i -ый проводник с q_i зарядом, когда вокруг i -го проводника с q_i зарядом отсутствуют окружающие (n -1) - проводников с q₁, q₂,…, q_{(n -1)} зарядами.

Раскрываем первую и вторую суммыв (5.144) с учётом (5.137) и (5.143) для случая

n -проводников, находящихся в линейном изотропном диэлектрике с εотносительнойдиэлектрическойпроницаемостью или вакууме, и получаем следующее выражение: W = W_с + W_вз =

n n

= (1/2)∑q_iφ_сi + (1/2)∑q_iφ_i = (1/2)(q₁φ_с1 + q₂φ_с2 + …+ q_nφ_сn) + (1/2)(q₁φ₁ + q₂φ₂ + …+ q_nφ_n) =

i=1 i=1 = (1/2)[q₁(φ_с1 + φ₁) + q₁(φ_с2 + φ₂) + …+ q_n(φ_сn + φ_n),(5.145)

где (5.143) φ_с1 , φ_с2 , …φ_сn - собственный потенциал уединённогоi -го проводника с q_i зарядом, т.е. когда окружающие этот i -ый проводник остальные (n -1) проводники отсутствуют; φ₁ , φ₂ , …φ_n (5.137) - потенциал, создаваемый всеми (n -1) -проводниками с q₁, q₂,…, q_{(n -1)} зарядами, окружающими этот i -ый проводник с q_i зарядом в точке пространства, где располагается i -ый проводник с q_i зарядом.

Введём суммарные φ₁^*, φ₂^* , …φ_n^*потенциалы, имеющие следующий вид: φ₁^* = (φ_с1 + φ₁), φ₂^* = (φ_с2 + φ₂),…, φ_n^*= (φ_сn + φ_n),(5.146)

где φ₁^* = (φ_с1 + φ₁) - суммарный потенциалв точке пространства, где располагается 1 -ый проводник с q₁ зарядом; первое φ_с1 слагаемое φ₁^* суммарного потенциалапредставляетсобой (5.143) собственный потенциал уединённого1 - го проводника с q₁ зарядом,а второе слагаемоеφ₁ суммарного

φ₁^* потенциалапредставляетсобой(5.137)потенциал, создаваемый всеми (n -1) - проводниками q₂, q₃,…, q_n зарядами, окружающими этот 1-ый проводник с q₁ зарядом в точке пространства, где располагается 1 -ый проводник с q₁ зарядом.

В выражении (5.146) φ₂^* = (φ_с2 + φ₂),…, φ_n^*= (φ_сn + φ_n) - суммарные потенциалы, определяемых аналогично 1 - му проводнику с q₁ зарядом,в точках пространства, где располагаются 2 - ой…n - ый проводники соответственнос q₂, q₃, …, q_n зарядами.

Подставляем (5.146) в (5.145) и получаем следующее выражение W полной энергии системы из

n-проводников с q₁, q₂,…, q_n зарядами, учитывающих (5.143) W_с и (5.137) W_вз соответственно собственнуюэнергиюи энергию взаимодействия этих n-проводников с q₁, q₂,…, q_n зарядами:

n

W = (1/2)∑q_i φ_i^*,(5.147) i=1

где (5.146) φ_i^*- суммарный потенциалв точке пространства, где располагается i-ый проводник с q_i зарядом.

Электрическая энергия плоского конденсатора

Плоский(рис. 5.24) конденсатор имеет на каждой металлической обкладке, с линейнымиразмерами намного большими d зазора между ними, равные по величине и противоположные по знаку заряды, модуль q которых равен q = q₊ и q = - q_- .

Полная (5.144) W энергия 2-ухметаллических обкладок, т.е. 2-ухпроводников, с равными по

q модулю и противоположными по знаку q₊ и q_- зарядами при нахождении между этими металлическими обкладками тонкого линейного изотропного диэлектрика с ε диэлектрическойпроницаемостью в первом приближении состоит только из W_вз энергии взаимодействия этих 2-ухметаллических обкладок и поэтому согласно (5.137) имеет следующий вид:

n

W_вз = (1/2)∑q_iφ_i = (1/2)( q₊ φ₁ + q_- φ₂) = (1/2)(qφ₁ - qφ₂) = (1/2)q(φ₁ - φ₂) = qU/2,(5.148)i=1

где(5.137) φ₁ - потенциал, создаваемый обкладкой плоского(рис.5.24) конденсатора с q_- зарядом, в точке пространства, где располагается обкладка плоскогоконденсатора с q₊ зарядом; φ₂ - потенциал, создаваемый обкладкой плоскогоконденсатора с q₊ зарядом, в точке пространства, где располагается обкладка плоскогоконденсатора с q_- зарядом; φ₁ - φ₂ = U - разность потенциалов или напряжение между обкладками плоскогоконденсатора.

Согласно (5.125) выражению ёмкостиC = q/(φ₁ - φ₂) = q/U плоскогоконденсатора соотношение между энергией W и q зарядом, U напряжением, C ёмкостьюэтого плоского конденсаторас учётом (5.148)имеет следующий вид: W = qU/2 = U²C/2 = q²/2C. (5.149)

Энергия электростатического поля

Проекция E_Y на OY ось (рис.5.24) вектора E напряженности электростатического поля междупластинами плоскогоконденсатора связана (5.124) с U напряжениеммеждуэтими пластинами следующим выражением: U = E_Yd, (5.150) где d - расстояние междупластинами плоскогоконденсатора.

Подставляем (5.150) U = E_Yd напряжениемеждупластинами плоскогоконденсатора,

(5.125) C = ε₀εS/d ёмкостьэтого плоского конденсатораc S площадью пластин в (5.149) W = U²C/2

и получаем W_eэлектрическую энергию плоского конденсатора в следующем виде: W_e = E_Y²d² ε₀εS/2d = ε₀εE_Y²V/2 = w_eV, (5.151) где V = Sd - объём диэлектрика с εдиэлектрическойпроницаемостью, в котором с постоянной w_e = ε₀εE_Y²/2 плотностьюраспределена энергия электростатическогополя плоскогоконденсатора.

С учётом(5.87) связи вектора D электрического смещенияс вектором E напряжённости электростатическогополя D = ε₀ εE плотностьw_e энергии электростатическогополя плоскогоконденсатора из (5.151) имеет следующий вид: w_e = W_e/V = ε₀εE_Y²V/2V = ε₀εE_Y²/2 = E_YD_Y/2, (5.152) где D_Y - проекция на OY ось (рис.5.24) вектора D электрического смещения электростатическогополя между пластинам плоскогоконденсатора. Элементарная dW_eэнергия электростатическогополя dV малого объёма в диэлектрической линейной изотропнойсреде с ε относительной диэлектрическойпроницаемостью, в пределах которого w_eплотность энергии электростатическогополя постоянна, с учётом (5.152) имеет следующий вид: dW_e = w_edV = ε₀εE²dV /2.(5.153)Энергия W_e электростатическогополя в V объёме линейного изотропного диэлектрика с учётом (5.153) элементарной dW_eэнергии электростатическогополя dV малого объёма этого диэлектрика примет следующий вид: W_e = ∫dW_e = ∫w_edV = ∫(ε₀εE²/2)dV = ∫(ED/2)dV, (5.154) V V V V

где с учётом(5.87) связи D = ε₀εE вектора D электрического смещенияс вектором напряжённости E электростатическогополя, а также с учётом коллинеарностии одинакового направления вектора D электрического смещенияи вектора E напряжённости электростатическогополяскалярное произведение EDравно ε₀εE², т.е. ED = ε₀εE²; интегрированиев(5.154) проводится по всему V объёму линейного изотропного диэлектрика, в котором существует электростатическоеполе.

Согласно (5.154) плотностьw_e энергии электростатическогополя в линейной изотропнойсредедиэлектрика, т.е. количество энергииэлектростатическогополя, присутствующего в единице объёма этоголинейного изотропного диэлектрика, имеет следующий вид:

W_e = ∫w_edV = ∫(ED/2)dV ↔ w_e = ED/2, (5.155)