Поляризация диэлектриков в электростатическом поле. Свободные, поляризационные заряды в диэлектрике 3 страница
Теорема (5.17) Гауссадля NE потокавектора E напряженности электростатическогополя через замкнутую воображаемуюповерхность S0 площадью (рис.5.22, а, б) внутри проводника имеет следующий вид: ∫EdS = q/ε0 = 0, (5.100) (S0)
где равенство (5.100) нулюинтеграла имеет место потому, что подинтегральная функция,
|

с вектором E напряжённости электростатического поля D = ε0εE согласно пункту а), по которому у поверхности проводника этот векторнапряжённости E электростатическогополя имеет только En нормальнуюсоставляющую,вектор D электрического смещенияимеет тоже только Dn нормальнуюсоставляющую.
Поэтому в (5.89) скалярное DdS произведение вследствие наличия у поверхности проводника толькоDn нормальнойсоставляющей вектора D электрического смещенияравноDndS, т.е. DdS= DndS, и это выражение (5.89) принимает следующий вид: ∫DdS= ∫DndS = ∫ ρdV ↔
(S) (S) V
n
↔ ND = ∫ ρdV = ∑qi, (5.101)
V i = 1
n
где (рис. 05.0.22, а, б) S - площадь поверхности проводника; ∑qi - суммарный заряд на поверхности i = 1
проводника.
Заряд проводника и поляризационный заряд на поверхности диэлектрика, окружающего проводник
Нескомпенсированныезаряды (рис.5.22, а) с σ+ положительной или (рис.5.22, б) с σ - отрицательной поверхностнойплотностью располагаются на поверхностипроводника S площадью, поэтому в (5.101) интегрирование по V объёму можно заменить интегрированием по этой поверхности проводника S площадью, которая охватываетVобъём, вследствие чего выражение (5.101) принимает следующий вид: ∫ ρdV =∫ σdS.(5.102) V (S) Подставляем (5.102) в (5.101) и получаем следующее выражение для определения Dn проекции на направление (рис.5.22) внешней n нормали к поверхности проводника S площадьювектора
D электрического смещенияу поверхности этого проводника S площадью:
∫Dn dS = ∫σdS ↔ Dn = σ,(5.103) (S) (S)
где в случае нахождения на сфере (рис. 05.0.22, а)положительного с σ+ поверхностной плотностью заряда вектор D электрического смещенияимеет положительнуюDn проекциюна направление внешней n нормали к поверхности проводника; в случае нахождения на сфере (рис. 5.22, б)отрицательногос σ- поверхностной плотностью заряда вектор D электрического смещенияимеет отрицательнуюDn проекциюна направление внешней n нормали к поверхности проводника.
С учётом(5.85) D = ε0 εE связи вектора D электрического смещенияс векторомE напряжённости электрическогополявыражение (5.101) для En проекции на направление
(рис.5.22, а, б) внешней n нормали к поверхности проводника S площадью вектора
E напряжённости электростатическогополяу поверхности этого проводника S площадью принимает следующий вид: En = Dn/ε0ε = σ/ε0ε, (5.104) где ε - диэлектрическаяпроницаемость среды, окружающей поверхность проводника S площадью. Выражение (5.92) для вектора D электрического смещения на (рис.5.22, а, б) границе между диэлектриком с ε диэлектрическойпроницаемостьюи проводником с qсвободнымизарядами, имеющими σ поверхностнуюплотность, имеет с учётом равенства нулю внутри проводника векторовE напряжённостии D электрического смещения, т.е. в (5.92) D2n' = 0, имеет следующий вид: D2n' - D1n'= σ↔D n' = - σ, (5.105) где "D n'" -проекция на направление (рис. 5.22, а, б) внешней n' нормали к поверхности диэлектрика с ε относительной диэлектрическойпроницаемостью, окружающего поверхность проводника с
S площадью,вектора D электрического смещенияв этом диэлектрике.
Подставляем (5.86) ε0E + P = D выражение вектора D электрического смещенияв диэлектрике, как сумму векторовε0E напряжённостиэлектростатического поля и
P поляризованности диэлектрика в рассматриваемой точке объёма диэлектрика, преобразованное (рис.5.22, а, б) для проекций на направление внешней n' нормали к поверхности диэлектрика, в (5.103), вследствие чего имеет место следующее выражение: (ε0E n' + P n') = - σ. (5.106) Подставляем (5.70) P = ε0χE выражение вектора P поляризованности неполярногодиэлектрика и полярногов слабых электрических полях, пропорционального вектору E напряжённостиэлектростатического поля в этих диэлектриках, преобразованное (рис.5.22, а, б) для проекций на направление внешней n' нормали к поверхности диэлектрика, в (5.106), вследствие чего имеет место следующее выражение: [(ε0Pn'/ε0χ) + Pn'] = - σ ↔ {[Pn'/(ε - 1)] + Pn'} = - σ ↔ Pn' = - σ(ε - 1)/ε, (5.107) где Pn' - проекция (рис. 5.22, а, б) на направление внешней n' нормали к поверхности диэлектрика с ε относительной диэлектрическойпроницаемостью, окружающего поверхность проводника S площадью, вектора P поляризованности диэлектрика; σ - поверхностнаяплотность qсвободногозаряда на проводнике S площадью; χ = ε - 1 - (5.70) диэлектрическая восприимчивостьвещества диэлектрика.
Подставляем (5.75) σp = Pn' выражение связи σp поверхностнойплотностиполяризационныхзарядов диэлектрика с проекцией Pn' на внешнюю n' нормаль к поверхности диэлектрика, окружающего (рис.5.22, а, б) поверхность проводника S площадью, вектора P поляризованности, в (5.107), вследствие чего имеет место следующее выражение: σp = - σ(ε - 1)/ε.(5.108)
Согласно (5.108) в случае нахождения на сфере (рис.5.22, а)положительного q+ заряда с σ+ поверхностной плотностью на диэлектрике с ε относительной диэлектрическойпроницаемостью, граничащей с этой заряженной сферой, возникает отрицательный поляризационныйзаряд с σp-поверхностной плотностью.
Согласно (5.108) в случае нахождения на сфере (рис.5.22, б)отрицательного q- заряда с σ- поверхностной плотностью на диэлектрике с ε диэлектрическойпроницаемостью, граничащей с этой заряженной сферой, возникает положительный поляризационныйзаряд с σp+поверхностной плотностью.
Силы, действующие в вакууме на поверхность заряженного проводника
Нескомпенсированныезаряды (рис.5.23) с, например, σ+ положительной поверхностнойплотностью располагаются на поверхностипроводника малой ΔS площадью, а вокруг этой поверхностипроводника расположена в вакууме, например, заряженная сфера тоже с
σ+ положительной поверхностнойплотностью. Поэтому от окружающих со всех сторон, например, положительных зарядов, расположенных на сфере с σ+ положительной поверхностнойплотностью, вектор E0 напряжённости электростатического поля имеет величинуE0 модуля с внутренней и внешнейсторонповерхностипроводника малой ΔS площадью, а направлен этот вектор
E0 напряжённостипо n нормали к поверхностипроводника малой ΔS площадью.
Вблизи (рис. 5.23) поверхностипроводника малой ΔS площадью Eσ+ модуль вектора Eσ+ напряжённости электростатического поля по аналогии (5.24) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля.Работа и потенциал электростатического поля"с напряжённостьюв вакууме электростатического поля бесконечной однородно заряженнойс σ+ положительной поверхностнойплотностью пластиной имеет следующий вид: Eσ+ = σ+/2ε0, (5.109)
где вектор Eσ+ напряжённости электростатического поля направлен с внешнейстороны вблизиповерхностипроводника малойΔS площадью по n нормали к поверхностиэтогопроводника, а с
|
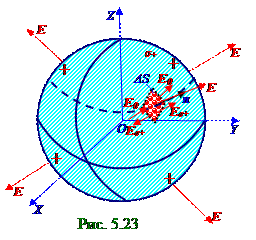
электростатического поля с учётом (5.109) имеет место следующее выражение: E0 = σ+/2ε0. (5.110)Вектор E напряжённости электростатическогополя(рис. 5.23) у поверхности сферы равен сумме коллинеарныхи направленных в одну сторону векторов Eσ+напряжённости электростатического поля вблизи поверхностипроводника малой ΔS площадью и E0 напряжённости электростатического поля от окружающих со всех сторон положительных зарядов, расположенных на сфере с σ+ положительной поверхностнойплотностью, вследствие чего для этого вектора E напряжённости электростатическогополяв вакууме у поверхности сферы и его Eмодуль имеет место с учётом (5.109), (5.110) следующее выражение:
E = Eσ+ + E0 ↔ E = Eσ+ + E0 ↔ E = σ+/ε0, (5.111) что (рис.5.22, а, б) соответствует (5.104)выражению вектора E напряжённости электростатическогополяу поверхности проводника S площадью, если этот проводник имеет
σ+ поверхностную плотность зарядов и εдиэлектрическаяпроницаемость среды, окружающей поверхность проводника, равна единице, т.е. вокруг проводника находится вакуум с ε = 1.
Вектор ΔF силы согласно (5.3) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля.Работа и потенциал электростатического поля", который действует со стороны электростатическогополя (рис.5.23) с вектором E0 напряжённости электростатического поля от окружающих со всех сторон положительных зарядов, расположенных на сфере, на
Δq = σ+ ΔS заряд, находящийся на поверхностипроводникамалой ΔS площадью с σ+ положительной поверхностнойплотностью, имеет с учётом (5.110), (5.111) следующий вид:
ΔF = ΔqE0 =ΔqE0n =n σ+ ΔSE0= nΔSσ+ 2/2ε0 = nΔSε0E2/2,(5.112) где E - модуль вектора E напряжённости электростатическогополяв вакууме у поверхности сферы; n - нормаль к поверхностипроводникамалой ΔS площадью, который находится на сфере, имеющей заряд с σ+ положительной поверхностнойплотностью.
Вектор Fед силы, который называют поверхностнойплотностью сил и который действует на площади единицу поверхности проводникамалой ΔS площадью, находящегося на сфере с σ+ положительной поверхностнойплотностью заряда, имеет с учётом (5.112) следующий вид:
Fед = ΔF/ΔS = nε0E2/2,(5.113)
где вектор Fед силы, действующий на единицу поверхности площади проводника, направлен по внешней n нормали к поверхностиэтогопроводникас σ+ положительной и σ- отрицательнойповерхностнойплотностью зарядов, поскольку в (5.113) присутствует квадрат модуля E модуля вектора E напряжённости электростатическогополяв вакууме у поверхности проводника, т.е. независимо от знака заряженного проводника сила, действующая на единицу поверхности проводника, является растягивающейсилой.
Вектор dFсилы, действующий на элементарнуюdSплощадь поверхности заряженного проводника, имеет с учётом (5.113) следующий вид: dF = Fед dS = nε0E2dS /2 =ε0E2dS /2,(5.114)
где dS = dSn - элементарный вектор площадиповерхности(5.15) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля" заряженного проводника.
Результирующий вектор F силы, действующий на Sплощадь поверхности заряженного проводника, имеет с учётом (5.114) следующий вид: F = (ε0/2) ∫E2dS,(5.115)
(S), S
где(S), S - площадь поверхности заряженного проводника, которая может замкнутой, тогда область интегрирования в (5.115) обозначается (S), и может незамкнутой, тогда область интегрирования в (5.115) обозначается S.
Электроемкость уединённой проводящей сферической поверхности
Потенциал φ уединённогопроводника пропорционален находящемуся нанём q заряду, вследствие чего имеет место следующее выражение: q = Cφ ↔ C = q/φ.(5.116) Коэффициент C пропорциональности в (5.1116) между φ потенциалом и q зарядом называется электроёмкостью. Согласно (5.116) ёмкостьC численно равна q заряду, сообщениекоторого проводнику повышает его φпотенциална единицу.
Согласно (5.57) проекция El вектора E напряжённости электростатическогополя на произвольное направлениеdl элементарного вектораперемещения в этом электростатическомполе равна скоростиубывания φ потенциала электростатического поля, которое численно равно приращению φ потенциалаэтого электростатического поля, взятого с противоположным знаком, на единицу длины в направлении dl элементарного вектораперемещения. Проведём интегрирование выражения (5.58) от l1 начальнойдо l2 конечной точек контура, где подинтегральной функцией является El проекция вектора E напряжённости электростатическогополя на произвольное направление dl элементарноговектораперемещения в электростатическомполе, вследствие чего имеет место следующее выражение: l2 El dl = - dφ ↔ φ1 - φ2 = ∫ Eldl.(5.117) l1
где φ1 - φ2 - разность потенциалов соответственно в l1 начальнойи l2 конечнойточках контура в электростатическомполе с вектором E напряжённости.
Сферическая(рис.5.22, а, б) поверхность R радиуса, заряжённая с постоянной
σ поверхностной плотностью, имеет n внешнюю нормальк этой сферической поверхности, направленную по r радиусу - вектору произвольной M точки пространствадиэлектрической среды, окружающей поверхность проводника с S площадью. Поэтому Dn проекция на направление внешней
n нормали к поверхности проводника S площадьювектора D электрического смещения совпадает с Dr проекцией на направление r радиуса - вектора этого вектора D электрического смещенияв произвольной M точке пространствадиэлектрической среды, окружающей поверхность проводника с S площадью. Вследствие этого выражение (5.101) принимает следующий вид для определения
Dr проекции на направление r радиуса - вектора D вектораэлектрического смещения в произвольной M точке пространствадиэлектрической среды, окружающей поверхность проводника с S площадью: ∫DdS= ∫DndS = ∫DrdS = q ↔ Dr4πr2 = q ↔ Dr = q/4πr2, (5.118) (Sr) (Sr) (Sr) где (рис.5.22, а, б) r - расстояние от центра сферыR радиуса до произвольной M точки пространствадиэлектрической среды, окружающей поверхность проводника с Sr площадью, при r ≥ R;q -свободный заряд проводника, который присутствуеттолько на сферической поверхности этого проводника 4πR2 площадью c σповерхностной плотностью, равной q/4πR2, т.е. σ = q/4πR2; Sr - площадь по теореме (5.20) Гаусса замкнутой воображаемойсферической поверхности, равной 4πr2, т.е. Sr = 4πr2, на которой находится произвольная M точка пространствадиэлектрической среды и которая охватываетповерхность проводника с S площадью с q свободным зарядом.
С учётом(5.87) связи D = ε0εE вектора D электрического смещенияс вектором
E напряжённости электростатическогополяEr проекция на направление r радиуса - вектора E векторанапряжённостиэтого электростатическогополя в произвольной M точке пространствадиэлектрической среды, окружающей (рис.5.22, а, б) поверхность проводника с S площадью,имеет следующий вид: Er = Dr/ε0ε = q/4πε0εr2, (5.119) где ε - относительная диэлектрическаяпроницаемость диэлектрика, окружающего(рис.5.22, а, б) сферическуюповерхность R радиуса; q -свободный заряд проводника, который присутствуеттолько на сферической поверхности этого проводника 4πR2 площадью c σповерхностной плотностью, равной q/4πR2, т.е. σ = q/4πR2.
Производим с учётом (5.110) интегрирование (5.112) от начального r1 = R значения радиуса, равного радиусу заряжённой с постоянной σповерхностной плотностью сферическойповерхности, до конечного r2 = ∞ значения радиуса бесконечно удалённой точки в электростатическомполе этойсферическойповерхности с учётом равенстванулю φ2потенциалав бесконечности, т.е. φ2 = 0. Получаем после интегрирования (5.112) следующее значение φпотенциаласферическойповерхности (рис.5.22, а, б) R радиуса, заряжённой с постоянной σповерхностной плотностью: ∞ ∞
φ1 - φ2 = ∫ Erdr= (q/4πε0ε)∫dr/r2 ↔ φ = q/4πε0εR.(5.120) R R Подставим (5.120) в (5.116) и получим следующее значение Cёмкости уединённой проводящей сферическойповерхности (рис. 05.0.22, а, б) R радиуса, помещённое в диэлектрическую средус εдиэлектрическойпроницаемостью: C = 4πε0εR. (5.121) За единицу ёмкости - Фарада[Ф] принимают ёмкость такого проводника, потенциалкоторого изменяется на 1 В при сообщении ему заряда в 1 Кл, вследствие чего для определения единицы ёмкости имеет место следующее выражение: 1 Ф = 1 Кл/1 В.(5.122)
Емкость плоского конденсатора
|

двумя разноимённо заряженными пластинами S площади с σ поверхностной плотностью имеет с использованием выражения (5.118) следующий вид: ∫DdS= ∫DYdS = q ↔ DYS = q ↔ DY = q/S, ↔ (Sd) (Sd)
↔ EYεε0= q/S ↔ EY = q/εε0S ↔ EY = σS/εε0S ↔ EY = σ/εε0, (5.123)
где DY- проекция на OY ось D вектораэлектрического смещения, имеющего толькосоставляющуюпоOY оси, в пространстведиэлектрической среды между левойи правой обкладками плоского конденсатора; Sd - площадь по теореме (5.20) Гауссавоображаемойплоской поверхности, равной S, т.е. Sd = S, которую по перпендикулярному направлению пересекает D векторэлектрического смещения и которая охватывает левуюобкладкус q = σ+S свободным зарядом; ε - относительнаядиэлектрическаяпроницаемость диэлектрикамежду левойи правой обкладками плоского конденсатора.
Интегрирование (5.123) с использованием (5.117) от O началакоординат (рис. 5.24),
где находится положительно заряженная с σ+ поверхностной плотностьюпластина, до отрицательнозаряженной с σ- поверхностной плотностьюпластины, находящейся на d расстоянии от Oначалакоординат, приводит к следующему выражению φ1 - φ2 разности потенциаловмежду этими пластинами: d d φ1 - φ2 =∫EYdx = EY∫dx = EYd = qd/ε0εS.(5.124) 0 0 Из (5.124) приходим к следующему выражению Cёмкостиплоскогоконденсатора с линейнымиразмерами обкладок намного большими d зазора между ними и ε диэлектрическойпроницаемостьюдиэлектрика между этими обкладками: C = q/(φ1 - φ2) = ε0εS/d. (5.125) ЁмкостьC [ф] плоскогоконденсатора численно равна q [Кл] заряду, при сообщении которого плоскомуконденсатору φ1 - φ2 разность потенциаловмежду пластинами повышается на 1 [В].
Емкость коаксиального конденсатора
В коаксиальном конденсаторе(рис. 5.25)внутреннийцилиндр R1 радиусом заряжен (5.8) с положительной τ+ линейнойплотностью зарядов, а внешнийцилиндр R2 радиусом, имеющий с внутреннимцилиндром единую OX ось, заряжен с отрицательной τ- линейнойплотностью зарядов.Длина l конденсатора намного больше R2 - R1 зазорамежду внутренними внешнимцилиндрами. Между внутренними внешним цилиндрами находится диэлектрикс ε диэлектрическойпроницаемостью. С учётом величины q = τl заряда навнутреннемцилиндре
l длиной Er проекцияна направление r радиуса - вектора вектораE напряжённости
Дата добавления: 2016-02-14; просмотров: 938;
