Исследование интерференционного светофильтра
Цель работы – научиться определять основные характеристики интерференционного светофильтра и практически применять его в работе.
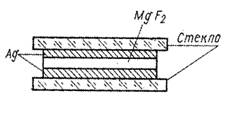 |
Исследуемый интерференционный монохроматический светофильтр (ИФ) работает на принципе многолучевой интерференции. Теория ИФ такая же, как у интерферометра Фабри – Перо. Фильтр выполнен в виде двух плоскопараллельных пластин, внутренние поверхности которых имеют высокоотражающие металлические покрытия, между которыми расположен слой диэлектрика с толщиной, сравнимой с длиной волны [1].
Рис.1. Устройство интерференционного фильтра
Основными характеристиками светофильтра являются:
lmax – длина волны в максимуме полосы пропускания.
Тmax – коэффициент пропускания в максимуме фильтра.
Тmin – минимальный коэффициент пропускания фильтра.
dl0.5 – спектральная полуширина – ширина полосы на уровне 0,5 Тmax.
2dq –апертура ИФ или угловая ширина светового пучка, при которой полуширина полосы пропускания фильтра dl0.5 меняется несущественно.
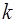 (контраст) – отношение коэффициентов пропускания в минимуме и максимуме ИФ:
(контраст) – отношение коэффициентов пропускания в минимуме и максимуме ИФ: 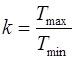 .
.
Обозначим пропускание, отражение и поглощение металлического слоя (например, Ag) через T , R и A соответственно, причем T+R+A=1. Для слоя диэлектрика (MgF2) примем пропускание равным T1.
Коэффициент пропускания Tl ИФ будет равен:
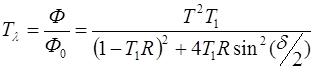 , (1)
, (1)
где Ф0 и Ф – падающий и прошедший через ИФ потоки излучения.
Таким образом, Tl является периодической функцией разности фаз 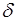 между интерферирующими лучами.
между интерферирующими лучами.
Из анализа уравнения (1) можно получить основные параметры ИФ.
Максимальное пропускание (рис. 2) определяется из (1) и при 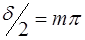 , m = 1,2,3… , и равна
, m = 1,2,3… , и равна
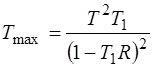 (2)
(2)
Положим T1 = 1 и учитывая, что T+R+A=1, получим:
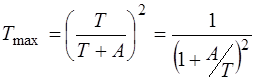 (3)
(3)
Для металлических слоев А¤Т ³ 0,5, поэтому Тmax£ 0,5.
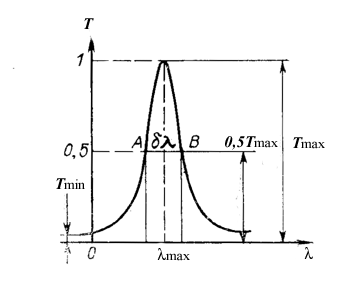
Рис. 2. Полоса пропускания интерференционного фильтра
Минимальное пропускание Тmin получаем, подставляя в (1) соотношение 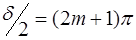 :
:
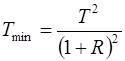 (4)
(4)
Положение максимумов lmax определяется величиной 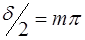 и
и
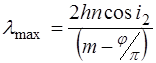 ,(5)
,(5)
где h – толщина, n – показатель преломления промежуточного слоя, m – порядок интерференционного максимума, а j – скачок фазы при отражении на границе “диэлектрик – покрытие”.
Видно, что при низких порядках интерференции m на положение lmax существенно влияют скачок фазы j. Если j ¤p <<1, то lmax определяется только оптической толщиной центрального слоя ИФ:
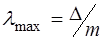 , m = 1,2,3… (6)
, m = 1,2,3… (6)
Из уравнения (6) видно, что ИФ имеет ряд максимумов, длины волн которых равны
lmax,1=D/1,lmax,2 =D/2, lmax,3=D/3 и т.д. (или lmax,1; lmax,2 = lmax,1 ¤ 2 ; lmax,3 =lmax,1 ¤ 3 ;……..lmax,m = lmax,1 ¤ m) .
С учетом этого ИФ называются фильтрами первого, второго, третьего и так далее порядков (рис. 3).
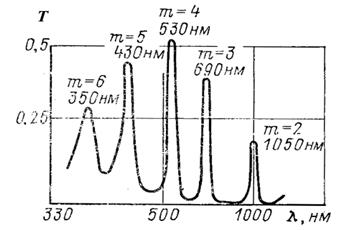
Рис. 3. Кривая спектрального пропускания ИФ
Ширина полосы пропускания dl0.5. За ширину полосы пропускания ИФ принимается величина горизонтального отрезка AB (рис.2) и обозначается как dl0.5.
Полуширина dl0.5 является функцией коэффициента отражения и задается соотношением
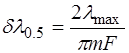 , где
, где 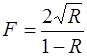 называется фактором резкости.
называется фактором резкости.
Изменение угла падения i1света на ИФ (или угла преломления i2 в центральном слое) влияет на lmax, см. (5), и на полуширину максимума dl0.5.
Из (5) видно, что наклон падающего пучка приводит к смещению lmax в коротковолновую сторону спектра ( поскольку cosi2 < 1). Кроме того, скачки фаз j^ и j|| для составляющих естественного света с колебаниями электрического вектора перпендикулярно и параллельно плоскости падения при наклонном падении не равны между собой и быстро меняются с ростом угла i1. Вследствие этого для взаимно перпендикулярных компонент поляризованного света максимумы lmax^ и lmax|| будут смещены друг относительно друга. В результате происходит расщепление полосы пропускания lmax.
Допустимая апертура падающего пучка 2i1. Апертура пучка влияет на ширину интерференционных максимумов, выделяемых ИФ, и увеличивает значение величины dl0.5. Можно показать, что допустимое уширение максимума dl связано с апертурой падающего пучка 2i1 соотношением
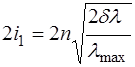 , (7)
, (7)
где n – показатель преломления промежуточного слоя. Задание
1. Исследовать ход спектрального коэффициента пропускания ИФ в области спектра 460 – 800 нм при нормальном падении света.
2. Измерить спектральный коэффициент пропускания ИФ в области спектра 460 – 560 нм через 10 нм при нормальном падении света.
3. Определить смещение исследуемого максимума lmax и изменение полуширины dl0.5 для угла падения света i1=20°.
4. Измерить спектральный коэффициент пропускания ИФ в области исследуемого максимума при i1=45° для естественного света и света, поляризованного перпендикулярно и параллельно плоскости падения. Измерения проводить через 5 нм в указанном интервале длин волн.
5. По экспериментальным данным построить графики зависимостей Тl =f(l) при i1= 0, 20, 45° и Т^ ,úú (l) =f(l) при i1=45°.
Примечание: указанные интервалы длин волн справедливы для конкретного ИФ, используемого в данной работе, и могут изменяться в зависимости от выбранного образца. Перед проведением лабораторной работы необходимо уточнить у преподавателя измеряемый спектральный диапазон.
Дата добавления: 2016-03-20; просмотров: 1873;
