Устойчивость линейных систем

Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения.

Устойчивая САУ — система, в которой переходные процессы являются затухающими.

Рассмотрим:

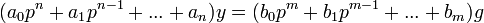— операторная форма записи линеаризированного уравнения.

y(t) = y_уст(t)+y_п = y_вын(t)+y_св

y_уст(y_вын) — частное решение линеаризированного уравнения.

y_п(y_св) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть

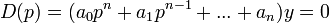
САУ устойчива, если переходные процессы у_n(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть 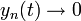при

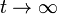
Решая дифференциальное уравнение в общем случае, получим комплексные корни

p_i, p_i+1 = ±α_i ± jβ_i

Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:

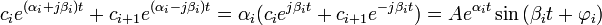, где

,

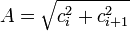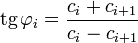
Из полученных результатов видно, что:

1. при ∀α_i<0,

выполняется условие устойчивости, то есть переходный процесс с течением времени стремится к у_уст (теорема Ляпунова 1);

2. при ∃α_i>0,

выполняется условие неустойчивости (теорема Ляпунова 2), то есть 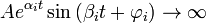, что приводит к расходящимся колебаниям;

3. при ∃α_i=0 и ∃α_i>0,

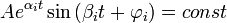, что приводит к незатухающим синусоидальным колебаниям системы (система на границе устойчивости) (теорема Ляпунова 3).