Тема 20. ПРИНЦИПЫ МАКСИМИЗАЦИИ ПРИБЫЛИ

1. Максимизация прибыли при совершенной конкуренции

2. Максимизация прибыли при несовершенной конкуренции

1. Максимизация прибыли при совершенной конкуренции. В условиях совершенной конкуренции предприниматель не может повлиять на рыночные цены, поэтому каждая дополнительная произведенная и проданная единица продукции приносит ему предельный доход MR= P1 (рис. 20.1).

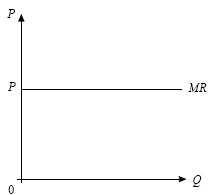
Рис. 20.1. Равенство цены и предельного дохода в условиях совершенной конкуренции

P – цена;

MR – предельный доход;

Q – объем производства товара.

Фирма расширяет производство лишь до тех пор, пока ее предельные издержки (МС) ниже дохода (MR), в противном случае она перестает получать экономическую прибыль P, т. е. до MC= MR. Так как MR= P, то общее условие максимизации прибыли может быть записано:

MC = MR = P (20.1)

где MC– предельные издержки; MR– предельный доход; P– цена.

2. Максимизация прибыли при несовершенной конкуренции. В условиях несовершенной конкуренции критерий максимизации прибыли отличается от рассмотренного, так как фирма может влиять на рыночную цену.

Для того чтобы продать дополнительную единицу продукции, фирма снижает цену. Это, как правило, дает некоторый эффект увеличения продаж, но одновременно фирма несет и потери из-за того, что все покупатели платят теперь более низкую цену. Этот относительный убыток снижает предельный доход MR, и поэтому он не совпадает с рыночной ценой, т. е.

MR не равно Р.

Вместе с тем условия максимизации при совершенной и несовершенной конкуренции имеют и общее между собой:

MC= MR, так как фирмы при qлюбых условиях производят дополнительную единицу продукции, если получают дополнительный доход, превышающий дополнительные издержки (рис. 20.2).

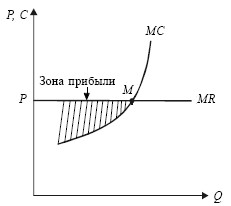
Рис. 20.2. Прибыль фирмы

C – издержки; P – цена.

В общем виде максимизация прибыли в условиях несовершенной конкуренции представляет собой:

МС = MR= P= АТС, (20.2)

где МС – предельные издержки; MR– предельный доход; АТС – средние общие издержки; P– цена.

По этому общему правилу максимизируется прибыль как в условиях монополии, олигополии, так и при полипо-лии, но в каждой из них имеются свои специфические особенности.