Объем призмы и цилиндра
1. Дидактическое оснащение практического занятия:
Теория по ссылке: Площадь поверхности и обьём призмы,
Объём и площадь поверхности цилиндра
| Определение Площади боковой поверхности призмы | Площадью боковой поверхности призмы называется сумма площадей всех боковых граней призмы. Площадь боковой поверхности прямой призмы Sбок.=Pосн.⋅H, где H — высота призмы. Pосн.- периметр основания |
| Площадь полной поверхности призмы | Площадь полной поверхности призмы — сумма площадей всех граней призмы. Она состоит из площади боковой поверхности и площади оснований Sполн.=Sбок.+2⋅Sосн. |
| Площадь полной поверхности куба | Все грани куба — квадраты, поэтому рациональнее использовать формулу Sполн. пов. куба=6⋅a2 гдеа-ребро куба |
| Объем прямой призмы | Объём прямой призмы находится по формуле: V=Sосн.⋅H |
| Объем прямоугольного параллелепипеда | Для прямоугольного параллелепипеда можно использовать формулу V=abc , где a, b, c — измерения прямоугольного параллелепипеда (длина, ширина, высота). |
Измерения цилиндра
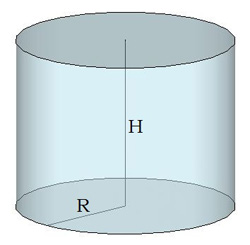

| Площадь поверхности цилиндра состоит из площади боковой поверхности и площади оснований цилиндра. Площадь боковой поверхности цилиндра S(бок.)=2πRH, где R — радиус цилиндра, H — высота цилиндра. Развёртка боковой поверхности цилиндра на плоскости — прямоугольник. Одна сторона прямоугольника является высотой цилиндра. AB=H Вторая сторона прямоугольника является длиной окружности основания цилиндра. AD=2πR Площадь полной поверхности цилиндра равна: S(полн.)=2S(осн.)+S(бок.)=2πR2+2πRH=2πR(R+H) Объём цилиндра находится по формуле: V=Sосн.⋅H V=π⋅R2⋅H , где R- радиус основания цилиндра |
| Важные формулы нахождения площадиn-угольников | 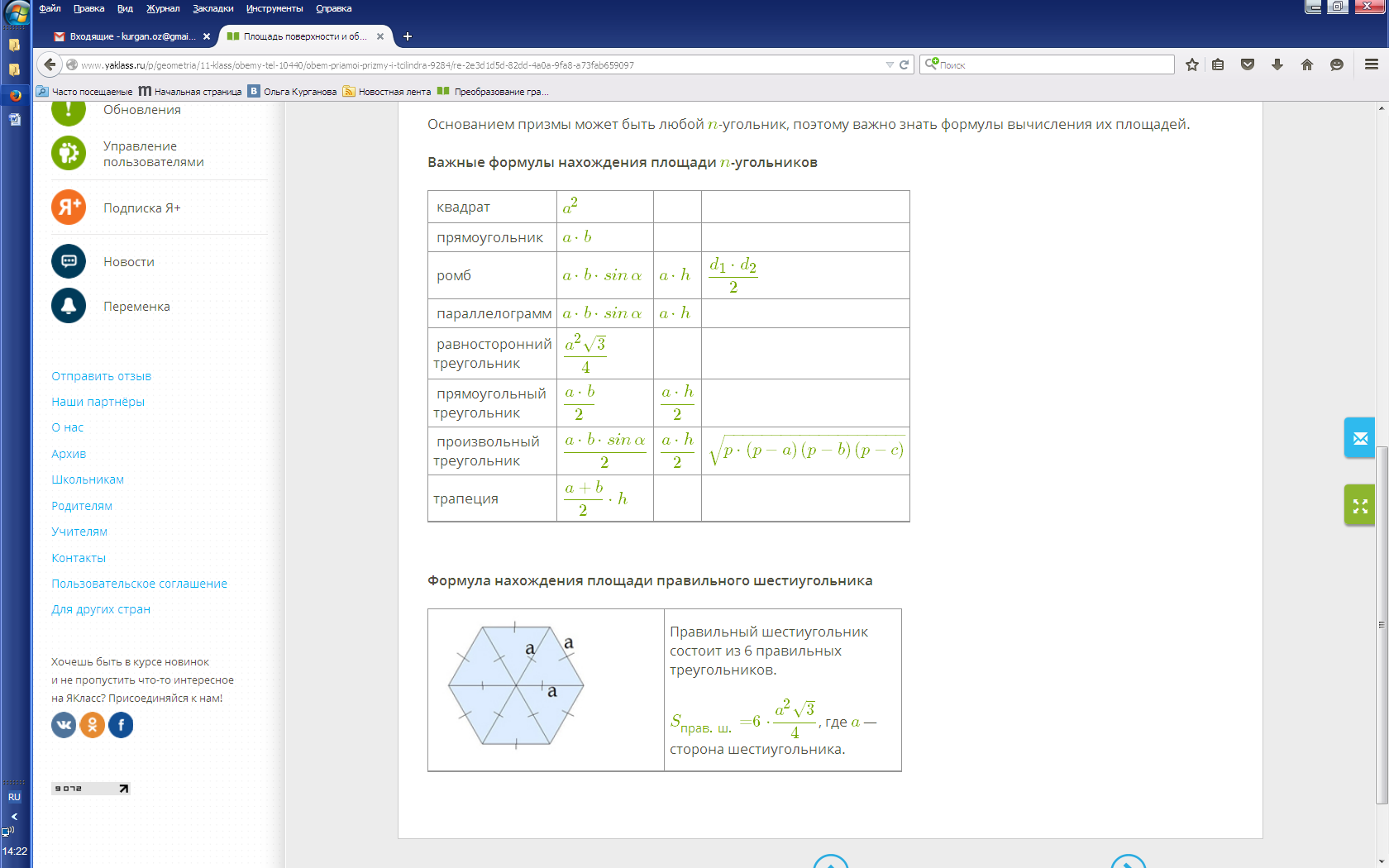
|
| Формула площади правильного шестиугольнока | 
|
Задания
Задание№1. Изменение объёма цилиндра
| Объём цилиндра равен 225см3. Радиус основания цилиндра уменьшили в 5 раз; высоту цилиндра увеличили в 8 раз. Вычисли объём полученного цилиндра. | ||

| Дано: V1 цилиндра=225см3 R2= R1/5 H2=8H1 Найти: V2 цилиндра-? | |
| Решение: Объём цилиндра вычисляется по формуле V=π⋅R2⋅H. По условиям задания V1=225. После всех изменений oбъём полученного цилиндра будет равен V2=π⋅(R1/5)2⋅(8⋅H1)=π⋅R12⋅H1⋅8/25=V⋅8/25=225⋅8/25=9⋅8=72см3 Ответ: V2=72см3 | ||
| Решить задание на ЯКласс | №1 Изменение объёма цилиндра | |
Задание №2 Объём цилиндра, полученного вращением квадрата
| Квадрат вращается вокруг своей стороны, которая равна 1см. Вычисли объём полученного тела вращения. | |
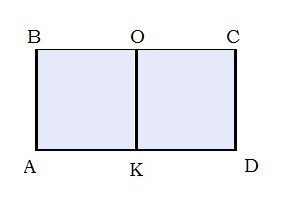
| Дано: ABCD–цилиндр R=AK=KD=1см ; H=CD=1см Найти:Vцилиндра-? |
| Решение: Квадрат вращается вокруг стороны OK. На рисунке — осевое сечение цилиндра ABCD. Объём вычисляется по формуле: V=πR2H R=KD=1см; H=OK=1см V=π⋅12⋅1=1πсм3 Ответ: V=πсм3 | |
| Решить задание на ЯКласс | №2 Объём цилиндра, полученного вращением квадрата |
Задание №3 Объём и площадь поверхности правильной призмы
Сторона основания правильной треугольной призмы равна 14см, высота призмы равна 15 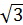 см. Вычисли объём и площадь поверхности призмы. см. Вычисли объём и площадь поверхности призмы.
| |
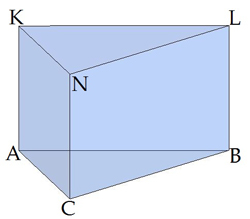
| Дано: ABCKLN –правильная треугольная призма
ABC- правильный треугольник
AB=BC=AC=14см
H=AK=15 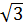 см.
Найти: V-? Sполн.-? см.
Найти: V-? Sполн.-?
|
Решение:
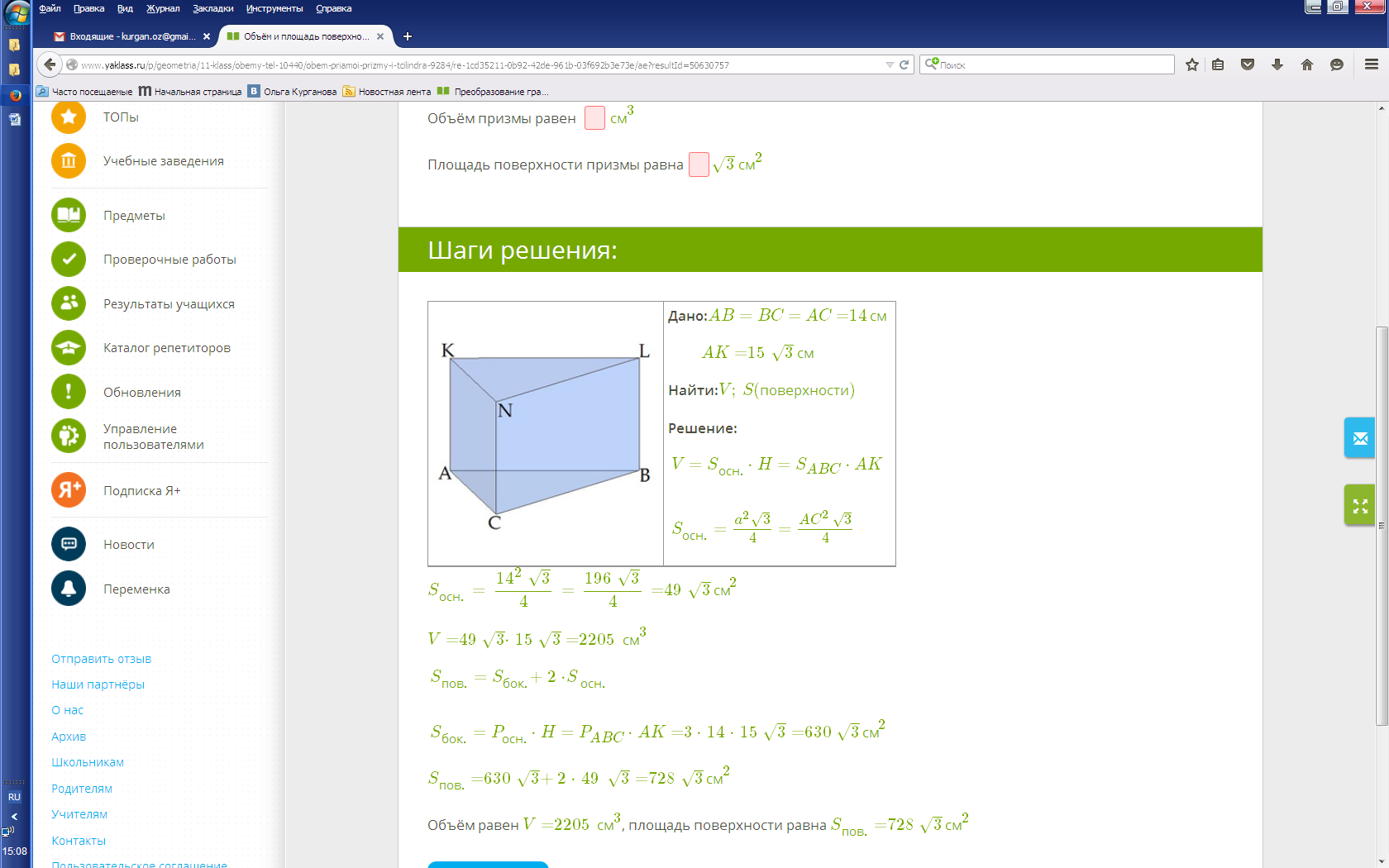
 Ответ: V=2205 см3Sполн.= 728
Ответ: V=2205 см3Sполн.= 728 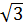 см3. см3.
| |
| Решить задание на ЯКласс | №3 Объём и площадь поверхности правильной призмы |
Задание №4 Объём призмы, в основании которой — ромб
| Основанием прямой призмы является ромб, диагонали которого равны 4см и 6 см. Большее диагональное сечение призмы равно 72см2. Вычисли объём призмы | |
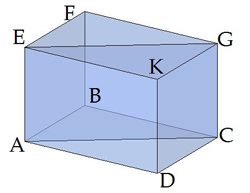
| Дано:ABCDEFGK- прямая призма ABCD и EFGK- основания призмы – ромб AEGC- большее диагональное сечение S AEGC=72см2. Найти: V-? |
Решение:
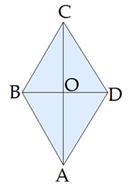 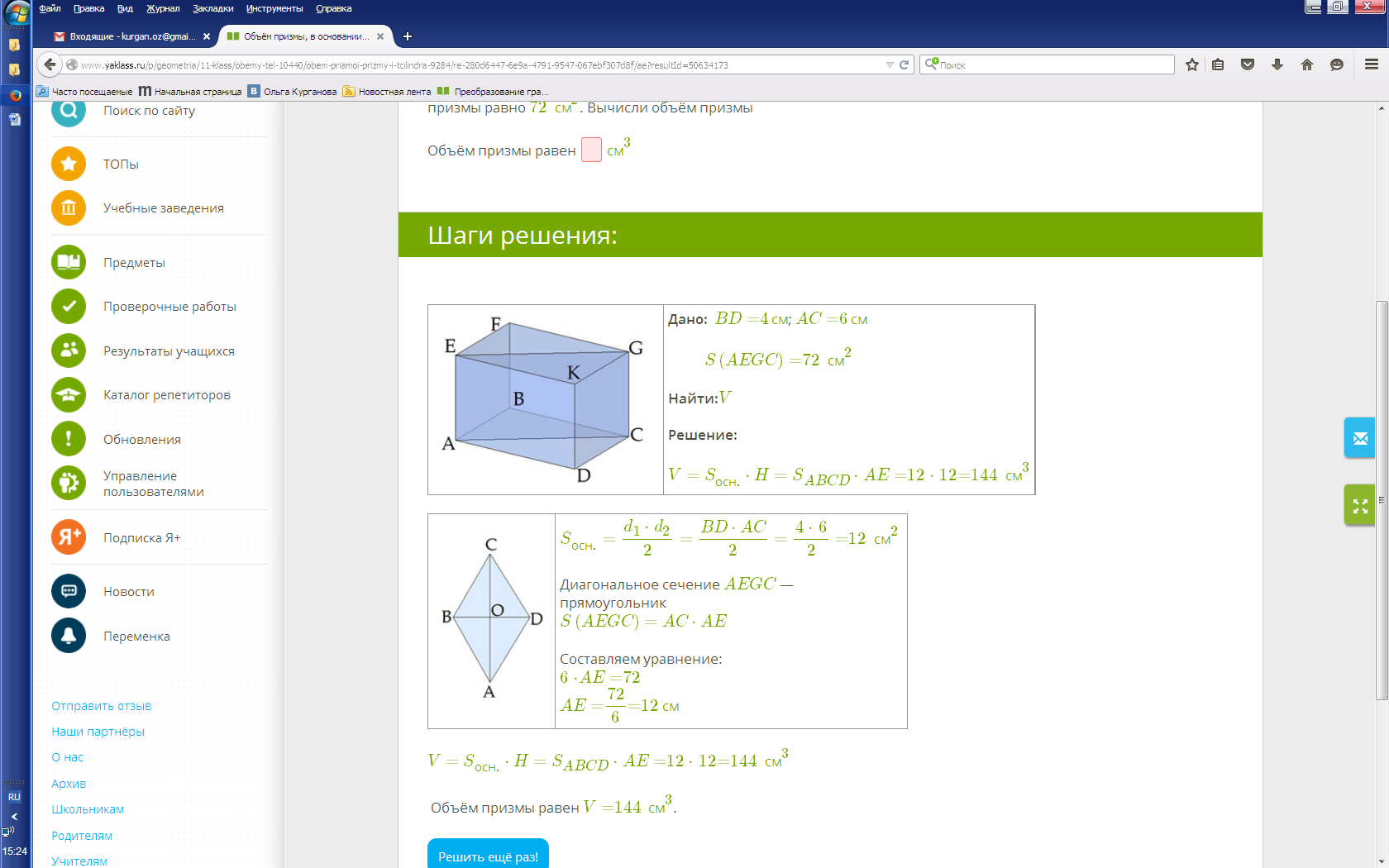

 Ответ: V=144см3
Ответ: V=144см3
| |
| Решить задание на ЯКласс | №4 Объём призмы, в основании которой — ромб |
Задание №5 Объём цилиндра, описанного около куба
| Вокруг куба описан цилиндр. Ребро куба равно 4см. Вычисли объём цилиндра. | |
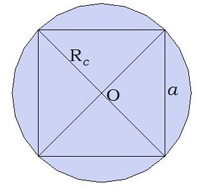
| .Дано: Цилиндр описан вокруг куба a=4 см Найти:Vцилиндра-? |
Решение:
V(цилиндра)=πR2H
Высота цилиндра H равна высоте куба — ребру куба a.
Поэтому H=4см.
Чтобы вычислить радиус цилиндра R, рисуем основания:
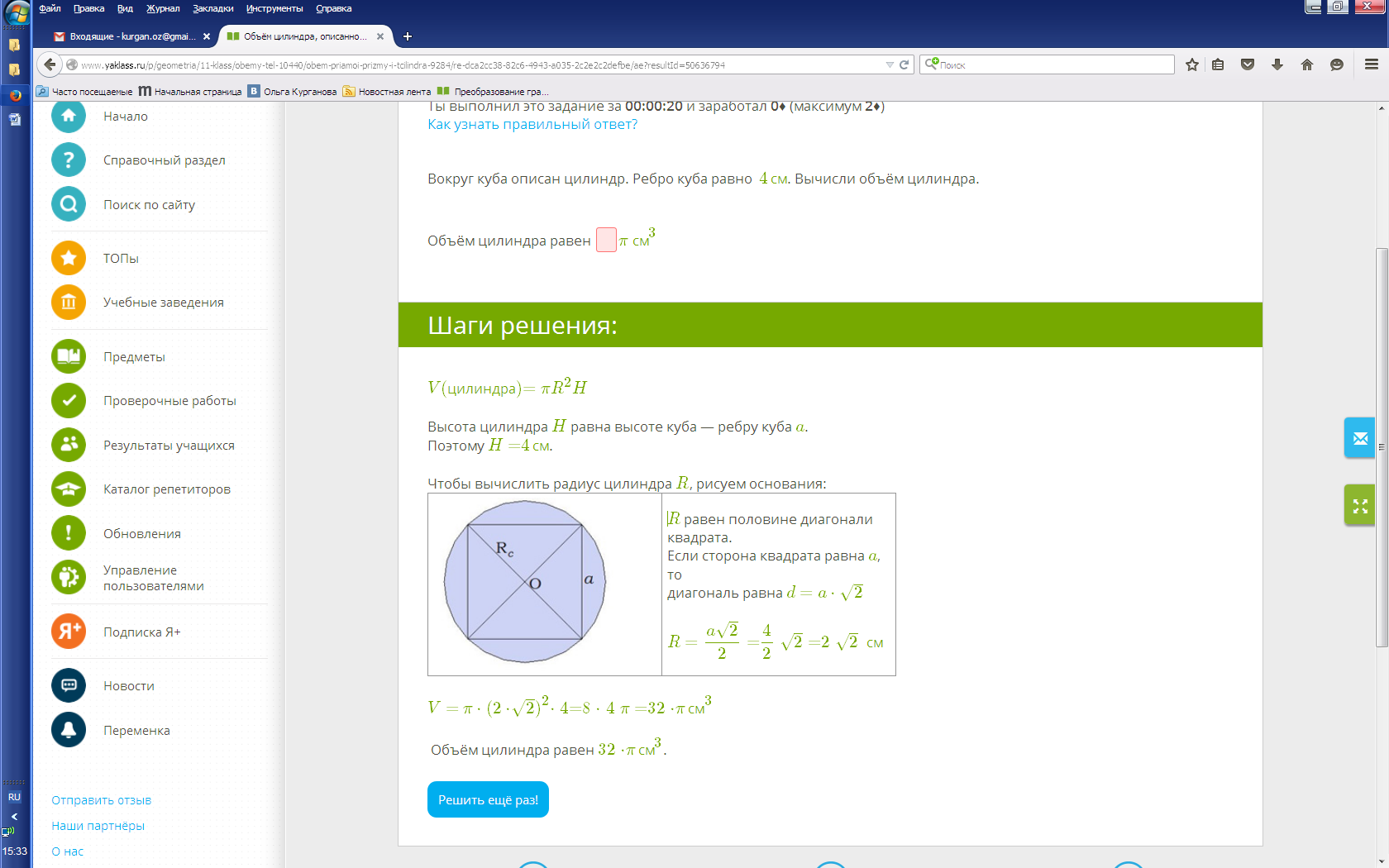
 Ответ: Vцилиндра=32⋅πсм3.
Ответ: Vцилиндра=32⋅πсм3.
| |
| Решить задание на ЯКласс | № 5 Объём цилиндра, описанного около куба |
Задание №6 Сечение, проведённое параллельно оси цилиндра
| В цилиндре параллельно оси проведено сечение, отсекающее от окружности основания дугу в 118 градусов. Угол между диагональю этого сечения и плоскостью основания цилиндра равен 60 градусов. Вычислить объём цилиндра, если радиус основания цилиндра равен 60 см. | |
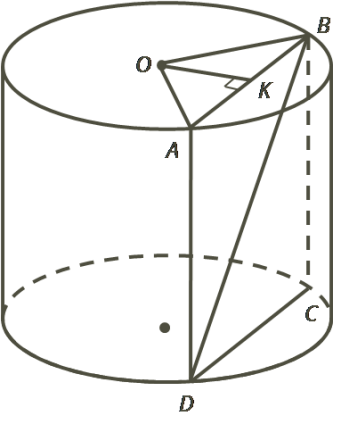
| Дано: Дуга AB=1180 ے BDC=600 R=60см Найти: Vцилиндра-? |
Решение:
Рассмотрим треугольник OBA.
∠AOK=12⋅∠AOB=59°
sin∠AOK=AKAO⇒AK=AO⋅sin∠AOK=60⋅sin59°
AB=2⋅AK=120⋅sin59°
Рассмотрим треугольник DCB.
tg∠BDC=BC/CD
BC=CD⋅tg∠BDC=120⋅sin59°⋅tg60°=120⋅ 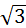 ⋅sin118°
Следовательно,
V=S(цилиндра)⋅H=π⋅R2⋅H=3600⋅π⋅120⋅ ⋅sin118°
Следовательно,
V=S(цилиндра)⋅H=π⋅R2⋅H=3600⋅π⋅120⋅ 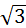 ⋅sin118°
V=432000 ⋅sin118°
V=432000 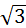 ⋅π⋅sin118°
Ответ: V=432000 ⋅π⋅sin118°
Ответ: V=432000 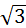 ⋅π⋅sin118° ⋅π⋅sin118°
| |
| Решить задание на ЯКласс | № 6 Сечение, проведённое параллельно оси цилиндра |
Содержание отчета
Записать конспект и решение заданий в тетрадь, ответить на контрольные вопросы
Контрольные вопросы
| Напишите основную формулу для нахождения объема прямой призмы и цилиндра | |
| Каким образом можно найти объем цилиндра , образованного вращением квадрата вокруг стороны, если известна сторона квадрата? Перечисли шаги решения. | |
| Каким образом можно найти объем правильной призмы, высота которой известна и: - в основании правильный треугольник со стороной a - в основании ромб со стороной a. Каких данных не хватает для решения этой задачи? |
| <== предыдущая лекция | | | следующая лекция ==> |
| Задание №4 Площадь сферы | | | ЧЕЛОВЕКА, ГОСУДАРСТВА И ОБЩЕСТВА 1 страница |
Дата добавления: 2016-03-15; просмотров: 3704;
