Задание№1. Исследование свойств функции
Теория по ссылке
Теорема 1
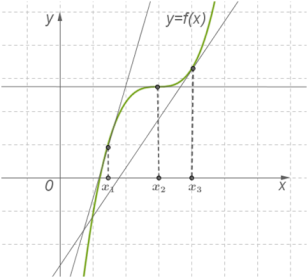
| Если во всех точках открытого промежутка X выполняется неравенство f′ʹ(x)≥0 (причем равенство f′ʹ(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке) , то функция y=f(x)) возрастает на промежутке X. |
Теорема2
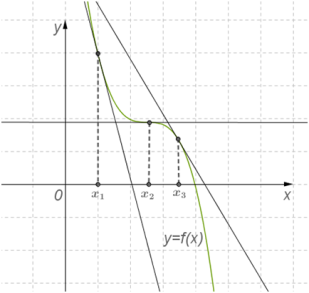
| Если во всех точках открытого промежутка X выполняется неравенство f′ʹ(x)≤0 (причем равенство f′ʹ(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция y=f(x) убывает на промежутке X. |
| Вывод | если существует производная функции в интервале (a,b) и в данном интервале 1) fʹ'(x)≥0, то функция в нём не убывает; 2) f'ʹ(x)≤0, то функция в нём не возрастает; 3) fʹ'(x)>0, то функция в нём возрастает; 4) f'ʹ(x)<0, то функция в нём убывает. |
| Теорема 3 | Если функция y=f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует. |
| Теорема 4 | (достаточные условия экстремума). Пусть функция y=f(x) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку x=x0. Тогда: а ) если у этой точки существует такая окрестность, в которой при x<x0 выполняется неравенство f'ʹ(x)<0, а при x>x0 — неравенство f'ʹ(x)>0, то x=x0 — точка минимума функции y=f(x)); б ) если у этой точки существует такая окрестность, в которой при x<x0 выполняется неравенство f'ʹ(x)>0, а при x>x0 — неравенство fʹ'(x)<0, то x=x0 — точка максимума функции y=f(x)) ; в) если у этой точки существует такая окрестность, что в ней и слева и справа от точки x0 знаки производной одинаковы, то в точке x0экстремума нет. |
| Алгоритм исследования непрерывной функции y=f(x) на монотонность и экстремумы: | 1. Найти производную f'(x). 2. Найти стационарные и критические точки. 3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. 4. Опираясь на теоремы 1, 2 и 4, сделать выводы о монотонности функции и о ее точках экстремума. |
| Точки экстремума | Точки экстремума - это точки , где функция меняет свое поведение с возрастания на убывание или наоборот (т. е. выпуклость или вогнутость). При переходе через точку максимума изменяется характер монотонности функции: слева от точки максимума функция возрастает, справа —убывает. При переходе через точку минимума изменяется характер монотонности функции: слева от точки минимума функция убывает, справа —возрастает. |
Задания
Задание№1. Исследование свойств функции
Используя данные о производной y=f′(x), приведённые в таблице, укажи:
(В ответе бесконечность пиши как Б с соответствующим знаком.) а) промежутки возрастания функции y=f(x): б) промежутки убывания функции y=f(x): в) точки максимума функции y=f(x): г) точки минимума функции y=f(x):
| ||||||||||||||||||||||||||||
Решение:
Достроим таблицу еще одной графой
Ответ:а) промежутки возрастания функции y=f(x): (−∞;−4) б) промежутки убывания функции y=f(x): (−4;−2) в) точки максимума функции y=f(x): x=-4 г) точки минимума функции y=f(x): x=-2 | ||||||||||||||||||||||||||||
| Решить задание на ЯКласс | №1 Исследование свойств функции |
12
Дата добавления: 2016-03-15; просмотров: 3884;