ОБЩИЕ ЗАДАЧИ МЕХАНИКИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА В БУРЕНИИ и РАЗРАБОТКЕ НЕФТЯНЫХ И ГАЗОВЫХ МЕСТОРОЖДЕНИЙ

К задачам механики деформируемого твердого тела в бурении относятся, прежде всего, задачи устойчивости стенок скважины, разрушения забоя, прочности труб и тампонажного камня, устойчивости и центрирования бурильных и обсадных колонн.

Следует отметить, что теория механики деформируемого твердого тела разработана достаточно полно, но она сложна, ее уравнения и граничные задачи намного сложнее, чем в гидромеханике. Требуется немало усилий, чтобы овладеть этой теорией и научиться правильно, ставить и решать граничные задачи.

В данной лекции невозможно охватить все многообразие математических моделей и методов решения задач механики деформируемого твердого тела. Приводем лишь наиболее простые, но широко используемые уравнения состояния, прочности и разрушения твердых тел, решения задач устойчивости стенки скважины для разных моделей горных пород и внешнего воздействия, развития горного давления на крепь скважины и задачи центрирования бурильных и обсадных колонн.

Все твердые тела в зависимости от диапазона нагружения и внешних условий в большей или меньшей степени проявляют свойства:

упругости – способности тела накапливать исчезающую при разгрузке деформацию;

пластичности – способности тела накапливать не исчезающую (остаточную) деформацию при разгрузке;

вязкости – способности тела накапливать деформацию во времени при постоянном напряжении или снижать напряжение во времени при постоянной деформации. Упругость и пластичность относятся к мгновенным свойствам тела, а вязкость – к его временным свойствам.

Обычно для изучения всех этих свойств и определения состояния тел на грани разрушения проводят простые опыты: осевое растяжение, сжатие, изгиб, сдвиг (срез или кручение) цилиндрических или призматических образцов в соответствии с методиками, принятыми общесоюзными или международными стандартами. По данным этих опытов строятся деформационные кривые, устанавливающие связь между соответствующими компонентами напряжений (или ), деформаций (или 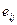), скоростей деформаций и времени t (см. лекцию 1).

Кроме того, определяют параметры предельного состояния, характеризующие разрушение материала. Все это служит основой для выбора определяющих математических моделей деформирования и разрушения твердых тел вообще, горных пород, цементного камня, материала обсадных и бурильных труб в частности.

Получить аналитическое решение задачи механики деформируемого твердого тела – значит определить прежде всего компоненты вектора перемещения 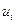, тензоров деформаций и напряжения 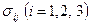в любой точке области D, занятой телом, и в любой момент времени.

В общем случае, как показано ранее, 15 искомых функций должны удовлетворять следующим 15 уравнениям.

Трем уравнениям движения [см. формулу (2.9)]

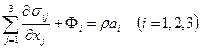. (3.93)

Шести уравнениям механического состояния

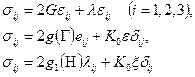(3.94)

соответственно при упругой деформации изотропного тела [см. формулу (2.74)]; при упругопластической деформации изотропного тела [см. формулу (2.77)]; при ползучести среды [см. формулу (2.91)]. Возможны уравнения другого вида, связывающие компоненты и , в зависимости от рассматриваемого состояния тела и действующих факторов (см. разд. 2.67).

Шести уравнениям совместимости (неразрывности) деформаций Сен-Венана [см. формулу (1.24)]

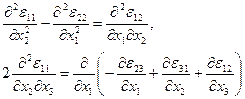(3.95)

и т.д. (остальные уравнения получаются круговой заменой индексов) при рассмотрении кратковременного напряженно-деформированного состояния тела. При изучении ползучести тела используются шесть аналогичных уравнений совместимости скоростей деформаций .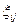

В уравнениях (3.93) – (3.95) использована декартова система координат 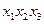и следующие введенные ранее обозначения: 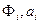- проекции массовых сил и ускорения; 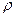- плотность тела; 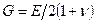- модуль сдвига; 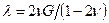- коэффициент Ламе; 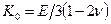- модуль объемного сжатия; Е, v – модуль Юнга и коэффициент Пуассона; 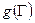и 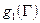- модули пластичности и ползучести, являющиеся соответственно функциями интенсивности деформации сдвига Г и интенсивности скорости деформации сдвига Н (см. раздел 1.3); - компоненты девиатора деформации; 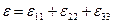- объемная деформация; 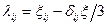- компоненты девиатора скорости деформации; 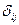- символ Кронекера:

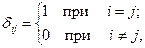
где 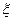- скорость объемной деформаци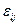и; и 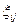- компоненты тензоров деформаций и скоростей деформаций; связанные соответственно с компонентами перемещения 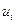и скорости 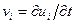соотношениями Коши:

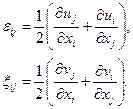(3.96)

При переходе к криволинейной системе координат вид всех уравнений, кроме уравнений (3.94), изменится. В разд. лекции 1 приведены формулы перехода к цилиндрической системе координат.

Для однозначного определения напряженно-деформированного состояния тела к уравнениям (3.93) – (3.95) необходимо присоединить начальное и граничные условия. Различают три основные граничные задачи механики деформируемого твердого тела.

Если на поверхности S, ограничивающей область D тела, задан вектор напряжения 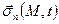, то граничные условия записываются в виде (см. разд. лекции 1)

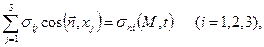(3.97)

где 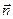- нормаль к поверхности S; 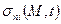- проекции вектора 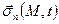на оси выбранной системы координат; М – точка поверхности; t – время.

В этом случае говорят о первой основной граничной задаче.

Если на поверхности S заданы условия для компонент вектора перемещения 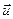(или скорости )

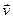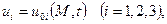(3.98)

то говорят о второй граничной задаче, где 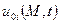- известные функции точек поверхности и времени.

В том случае, когда на одной части поверхности S задано условие вида (3.97), а на другой – вида (3.98), говорят о третьей основной граничной задаче, иногда ее называют смешанной граничной задачей.

Отличительная особенность первой основной граничной задачи состоит в том, что ее решение в зависимости от удобства можно строить в перемещениях (скоростях) или в напряжениях. Вторую и третью граничные задачи можно решать только в перемещениях (скоростях).

Решить задачу в перемещениях – значит представить исходную систему уравнений, граничные и начальные условия через функции 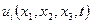. Для этого достаточно подставить формулы (3.94) и (3.96) в уравнения (3.93) и граничные условия (3.97). полученная таким образом система трех уравнений и трех граничных условий будет содержать только перемещения 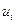. В этом случае надобность в уравнениях (3.95) отпадает. Они могут служить лишь для контроля полученного решения.

Если первая граничная задача решается в напряжениях , то эти функции, кроме уравнений (3.93), должны удовлетворять и системе уравнений (3.95), в которой необходимо (или 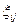) выразить через с помощью формул (3.94).

Ясно, что вид и характер исходной системы уравнений зависит от вида соотношений (3.94). С различными частными системами таких уравнений можно познакомиться по справочной литературе, учебникам и монографиям. При решении конкретных задач мы будем получать эти уравнения в упрощенном виде.

Определение напряженно-деформированного состояния тела не может быть самоцелью. Оно лишь предпосылка для оценки прочности, устойчивости, долговечности тела, конструкции или сооружения.