Бесключевые функции хэширования

Обычно требуется, чтобы бесключевые хэш-функции обладали следующими свойствами:

1) однонаправленность, (по Y = h(X) трудно определить X)

2) устойчивость к коллизиям, (по X трудно найти X’, такое, что h(X) = h(X’).

3) устойчивость к нахождению второго прообраза, (трудно найти пару X, X’ такие, что h(X) = h(X’))

Например, хэш-функция CRC-32, представляющая собой контрольную сумму, является линейным отображением и поэтому не удовлетворяет ни одному из этих трех свойств.

Использование в качестве бесключевой хэш-функции функции, построенной на основе алгоритма блочного шифрования в режиме выработки имитовставки, также нецелесообразно, так как обратимость блочного шифрования позволяет подбирать входное сообщение для любого значения свертки при фиксированном и общеизвестном ключе.

Для построения примера хэш-функции, удовлетворяющей свойству 1), рассмотрим функцию, заданную формулой g_k(x) = Е_k(х) Å х, где Е_k — алгоритм блочного шифрования. Такая функция является однонаправленной по обоим аргументам. Поэтому на ее основе можно построить хэш-функцию, определив одношаговую сжимающую функцию одной из следующих формул:

f(x, H) = E_H(x)Å x или f(х, Н) = Е_х(Н)Å Н.

Первая из этих функций лежит в основе российского стандарта хэш-функции, а вторая - в основе американского стандарта SHA.

Обе приведенные выше шаговые функции хеширования принадлежат семейству:

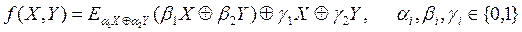
Не все функции данного семейства стойки к коллизиям. Стойкие к известным методам криптоанализа конструкции шаговых функций хеширования сведены в таблицу.

Таблица 8. Шаговые функции хеширования f(X, Y), использующие блочное шифрование E_k. (длина блока равна длине ключа или ключ дополнен до длины блока)

Трудоемкость подбора прообраза для однонаправленной функции или трудоемкость поиска второго- прообраза оцениваются величиной О(2ⁿ). В то же время трудоемкость поиска коллизии оценивается величиной О(2^n/2), так как в данной ситуации применима атака, основанная на парадоксе "дней рождений".

Значением любой из хэш-функций, построенных из приведенных одношаговых сжимающих функций, является вектор длины n, равной размеру блока. В случае если эта величина оказывается недостаточной, ее можно увеличить, заменив одношаговую функцию f на функцию f’ с удвоенной размерностью значений. Это можно сделать, например, путем двукратного применения функции f с последующим перемешиванием полублоков согласно формуле:

f’(x, H_l, H₂) = π(f(x, H_l), f(x, H₂)),

в которой π переставляет произвольные полублоки а, b, с, d по правилу π((a,b),(c,d)) = (a,d,c,b) . Такой подход реализован в конструкции одношаговой функции MDC-2.

Другие примеры бесключевых хэш-функций дают известные алгоритмы MD-4, MD-5 и SHA. Они оперируют с блоками длины n, совпадающей с длиной результирующего значения свертки, причем п = 128 для алгоритма MD-4 и п = 160 для MD-5 и SHA. Указанные алгоритмы спроектированы специально с учетом эффективной реализации на 32-разрядных ЭВМ.

При их использовании исходное сообщение М разбивается на блоки длиной т = 512 бит. Последний блок формируется путем дописывания к концу сообщения комбинации 10...0 до получения блока размера 448 бит, к которому затем добавляется комбинация из 64 бит, представляющая битовую длину сообщения. Затем вычисляется значение свертки с использованием одношаговой сжимающей функции, заданной формулой f(x, H)=E_x(H) Å H, где х - блок сообщения длины т = 512 бит, Н - блок из п бит, а Е_х - некоторое преобразование множества блоков. Значение начального вектора определяется в описании преобразования Е_х. В стандарте хэш-функции ГОСТ Р 34.11-94 приняты значения п = т = 512. Одношаговая сжимающая функция f(x,H), используемая для вычисления последовательности значений H_i = f(x_i, H_i-1), построена на базе четырех параллельно работающих схем блочного шифрования (ГОСТ 28147-89), каждая из которых имеет 256-битовый ключ и оперирует с блоками размера 64 бита. Каждый из ключей вычисляется в соответствии с некоторой линейной функцией от блока исходного сообщения x_i и значения H_i-1. Значение H_i, является линейной функцией от результата шифрования, блока исходного сообщения x_i, и значения H_i-1. После вычисления значения H_N для последовательности блоков M₁,M₂,..,M_N применяют еще два шага вычисления согласно формуле

H = h(M) = f(Z Å M_N, f(L, H_N)),

где Z — сумма по модулю два всех блоков сообщения, a L — длина сообщения.