Описание эксперимента

Тележка массой m_т движется ускоренно под действием силы натяжения Т нити, перекинутой через блок. Сила натяжения возникает за счет прикрепленных к нити грузов массойm_гр (рис. 1).

Если начальная скорость тележки υ₀ = 0, то из (2) следует, что ее перемещение (путь) определяется уравнением

S = at²/2. (4)

График функции S = f(t²) представляет собой прямую линию (рис. 2), тангенс угла наклона которой равен tg φ = ∆S/∆t = a/2. Исходя из этого, значение ускорения, с которым движется тележка, можно найти по формуле

a = 2 tg φ = 2∆S/∆t. (5)

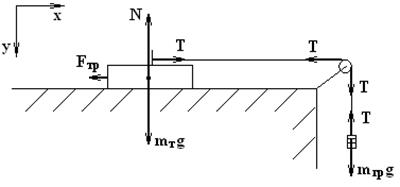
Рис.1. Груз на горизонтальной поверхности

Рассмотрим движение тележки по горизонтальной поверхности – треку (рис. 1). Рассчитаем ускорение тележки сначала без учета силы трения. Для этого применительно к тележке и грузу массой m_гр запишем 2-й закон Ньютона в векторном виде:

m_т a = T + N + m_тg;

m_гр a = m_гр g + T.

В проекциях на оси координат:

m_т a = T;

m_гр a = m_гр g – T. (6)

Решая систему уравнений (6), получим

a = m_гр g/( m_гр + m_т). (7)

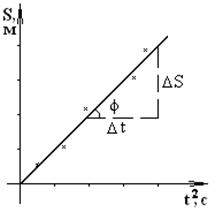
Рис. 2. График функции S = f(t²)

Теперь учтем силу трения (будем полагать, что, в основном, трение определяется взаимодействием скользящих друг о друга поверхностей валов тележки с ее деталями). Второй закон Ньютона в векторном виде запишем как

m_т a = T + N + m_тg + F_тр;

m_гр a = m_гр g + T.

В проекциях на оси координат:

m_т a = T – F_тр; (8а)

m_гр a = m_гр g – T. (8б)

Решая систему уравнений (8а) и (8б), получим

a = (m_гр g – F_тр) /( m_гр + m_т). (9)

Сила трения

F_тр = μN = μ m_тg, (10)

где N = m_тg – сила реакции опоры.

Для расчета коэффициента трения воспользуемся уравнениями (9) и (10):

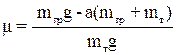. (11)

Перейдем к движению груза по наклонной плоскости (рис. 3).

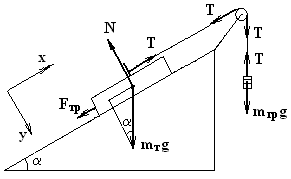
Рис. 3. Груз на наклонной плоскости

Рассчитаем ускорение тележки сначала без учета силы трения. Запишем
2-й закон Ньютона в векторном виде:

m_т a = T + N + m_тg;

m_гр a = m_гр g + T.

В проекциях на оси координат:

m_т a = T – m_тgsinα;

m_гр a = m_гр g – T. (12)

Решая систему уравнений (12), получим

a = g(m_гр – m_тsin α) /( m_гр + m_т). (13)

C учетом силы трения 2-й закон Ньютона в проекциях на оси координат:

m_т a = T – m_тgsinα – F_тр;

0 = N – m_тgcosα

m_гр a = m_гр g – T. (14)

Сила трения

F_тр = μN = μ m_тgcosα. (15)

Решая систему уравнений (14) c учетом (15), получим

a = g(m_гр – m_т(sinα + μ cosα)) /( m_гр + m_т). (16)

Формулу для расчета коэффициента трения получим из (15) и (16):

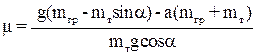. (17)