ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ МЕТОДОМ ОБОРОТНОГО МАЯТНИКА
Оборотный маятник используется для точного определения ускорения свободного падения. В основе этого метода определения ускорения свободного падения лежит теорема Гюйгенса: если физический маятник подвесить за центр качания О1, то его период не изменится, а прежняя точка подвеса О сделается новым центром качания[2, с.211] (рис.1).Оборотный маятник позволяет с точностью до 0,5% определить положение точки подвеса и центра качания. Расстояние между этими точками называется приведенной длиной физического маятника (оборотный маятник это частный случая физического маятника). Так как период колебаний физического маятника равен периоду колебаний математического маятника, если его приведенная длина равна длине математического маятника, то для определения ускорения свободного падения можно воспользоваться формулой математического маятника:
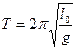 , (1)
, (1)
здесь Т – период колебаний физического маятника, l0 – его приведенная длина, g – ускорение свободного падения. Таким образом, определение ускорения свободного падения сводится к определению периода колебаний физического маятника и его приведенной длины.
Получим выражение (1), зная основной закон динамики вращения твердого тела относительно неподвижной оси вращения О:
I0 ε0=M0, (2)
здесь I0 – момент инерции твердого тела относительно данной оси О, ε0 – угловое ускорение относительно той же оси вращения, M0 – результирующий момент внешних сил относительно осиО. Все кинематические и динамические характеристики вращения твердого тела относительно неподвижной оси выбираются с надлежащим знаком [2, c.173]. Условимся величины, определяющие повороты по часовой стрелке выбирать со знаком «-»,против часовой стрелки со знаком «+».
Физическим маятником называют любое твёрдое тело, имеющее неподвижную ось вращения О, не совпадающую с центром масс тела (рис. 1). При отклонении маятника от положения равновесия на угол φ возникает возвращающий момент силы тяжести относительно этой оси
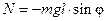 , (3)
, (3)
где m — масса тела, l — расстояние между осью вращения О и центром масс С («-» свидетельствует о том, что φ и N имеют противоположные знаки). В этом случае уравнение динамики вращательного движения твёрдого тела относительно оси запишется в виде:
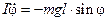 , (4)
, (4)
где I — момент инерции тела относительно оси вращения, 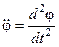 — угловое ускорение. При малых углах отклонения
— угловое ускорение. При малых углах отклонения 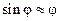 , тогда
, тогда
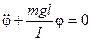 . (5)
. (5)
Сравнивая полученное уравнение с известным общим уравнением гармонических колебаний
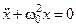 , (6)
, (6)
приходим к выводу, что физический маятник совершает свободные гармонические колебания с частотой и периодом соответственно
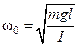 и
и 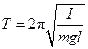 . (7)
. (7)
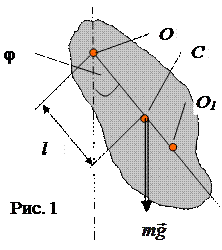
По теореме Штейнера I = Ic +ml2 , (8)
где Ic — момент инерции тела относительно оси, проходящей через цент масс C, l — расстояние между центром масс и действительной осью вращения.
,
 Обозначив
Обозначив
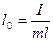 , (9) (20)
, (9) (20)
после подстановки (9) в (7) получаем интересующую нас формулу (1)
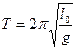 (1) (21)
(1) (21)
Как уже отмечалось, величина l0 называется приведенной длиной физического маятника. Поскольку (1) совпадает с периодом свободных колебаний математического маятника длиной l0, то под приведенной длиной физического маятника понимается длина такого математического маятника, период свободных колебаний которого совпадает с периодом свободных колебаний данного физического маятника.
Если отложить от точки подвеса О вдоль прямой ОС отрезок ОО1, длина которого равна приведенной длине физического маятника l0, то точка О1 станет центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений. Легко доказать (сделайте это самостоятельно), во-первых, что l0> l, т.е. точка подвеса и центр качания лежат по разные стороны от центра масс С, во-вторых, всем точкам подвеса одинаково удаленным от центра масс маятника С соответствует одна и та же приведенная длина, а следовательно один и тот же период колебаний Т. Точка подвеса и центр качания являются взаимными или сопряженными точками в том смысле, что если маятник подвесить за ту или другую точку, то в соответствии с теоремой Гюйгенса периоды колебаний совпадут (докажите это самостоятельно). Точка подвеса и центр качания находятся по разные стороны от центра масс и расположены асимметрично относительного него (доказательство см. в [2, с.213]). Физический маятник, который можно подвешивать за любую из сопряженных точек называется оборотным. Существуют разнообразные конструкции оборотных маятников.
ОПИСАНИЕ УСТАНОВКИ
Оборотный маятник в данной лабораторная установка показана на рис.2. Правый и левый болты с резцами треугольного сечения закрепляются на одинаковой высоте так, чтобы масса маятника распределялась равномерно по обеим точкам приложения нагрузки, и маятник находился в строго вертикальном положении. Для точного измерения ускорения свободного падения стол должен находиться в устойчивом положении.
Опорные втулки (А и В соответственно) прикрепляются по краям цилиндрического стержня.

Рис. 2 Экспериментальная установка «Оборотный маятник»
Период колебаний маятника определяется для малых амплитуд колебаний при помощи светового барьера. Переключатель на световом барьере должен быть установлен в крайнее правое положение  .
.
Идея метода
 Метод основан на определении приведенной длины физического маятника и соответствующих ей периодов колебаний, что позволяет рассчитать ускорение свободного падения по формуле (1).
Метод основан на определении приведенной длины физического маятника и соответствующих ей периодов колебаний, что позволяет рассчитать ускорение свободного падения по формуле (1).
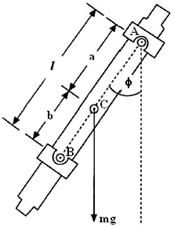
Оборотный маятник (рис.3) состоит из длинного цилиндрического стержня, на котором закрепляются две подвижные опорные втулки А и В. Колебания маятника осуществляются поочередно вокруг осей, проходящих через вырезы этих втулок.
Обозначим расстояние от выреза опорной втулки А до центра масс С через а; расстояние от выреза опорной втулки
В до центра масс С через b; расстояние между осями l.
Рис. 3 Оборотный маятник
Пусть ТА и ТВ – периоды колебаний маятника относительно осей, проходящих соответственно через вырезы опорных втулок А и В. В соответствии с формулой (7) можно записать:
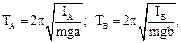 (10)
(10)
где IA и IB – моменты инерции маятника относительно осей, проходящих через вырезы опорных втулок.
Возведем каждое из выражений (10) в квадрат, умножим первое на а, второе – на b и вычтем второе уравнение из первого:
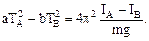 (11)
(11)
Моменты инерции IA и IB можно определить, воспользовавшись еще одной теоремой Штейнера: «Момент инерции тела относительно произвольной оси равен сумме двух слагаемых: момента инерции относительно параллельной ей оси, проходящей через центр масс IC, и произведения массы тела на квадрат расстояния между центром масс и рассматриваемой произвольной осью».
Таким образом,
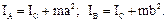 (12)
(12)
Подставив соотношение (12) в (11), получим:
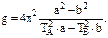 (13)
(13)
Если подобрать положения опорных втулок А и В таким образом, чтобы выполнялось соотношение ТА = ТВ = Т0, то формула (13) значительно упрощается, что позволяет получить рабочую формулу для определения ускорения силы тяжести при помощи оборотного маятника:
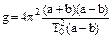
или уже знакомая нам формула (1), преобразованная относительно g
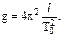 (14)
(14)
где l = a + b – расстояние между вырезами опорных втулок в случае равенства периодов колебаний относительно каждой из осей (ТА = ТВ = Т0) и есть приведенная длина оборотного маятника. Зная l и Т0 , по формуле (14) можно рассчитать ускорение свободного падения g.
Технические характеристики измерительных приборов установки
Таблица 1
| №п.п. | Название прибора | Пределы измерений | Число делений | Цена деления | Абсолютная погрешность |
| Счетчик колебаний | 0.01с | ||||
| Измерительная рулетка | 1 мм |
Выполнение работы
1. Опорные втулки А и В закрепите симметрично на расстоянии 7—10 см от концов стержня.
2. Установите маятник так, чтобы опорная втулка А служила осью качания. Отклоните маятник от положения равновесия на угол, не превышающий 20. Проведите 5—7 измерений периода колебаний ТА. Найдите среднее значение периода ТА.
3. Переверните маятник так, чтобы опорная втулка В стала осью качания оборотного маятника. При этом, не меняя положения втулки А, опорную втулку В установите на расстоянии l = 60 см от неё. Проведите 2—3 измерений периода колебаний ТВ. Найдите среднее значение периода ТВ. Результат занесите в таблицу 2.
Таблица 2
| l, см | … | |||
| ТВ, с |
4. Каждый раз, уменьшая расстояние между втулками на 2 см, проведите измерения ТВ и результаты измерений занесите в таблицу 2. Рекомендуемый диапазон расстояний между опорными втулками l: 60 - 34 см. Постройте график зависимости ТВ(l). Графически определите расстояния l1 и l2, для которых ТВ = ТА (см. пример рис.4).
5. Перемещения опорной втулки В приводят к изменению момента инерции маятника и положения его центра масс. Следовательно, и меняется значение периода колебаний относительно втулки А. Чтобы учесть эти изменения, необходимо провести измерение периодов колебаний ТА и ТВ при одинаковых значениях l. Для этого установите между втулками расстояние l = l1 – 3 см (положение втулки А не меняем). Определите поочередно периоды ТА и ТВ на выбранном расстоянии.
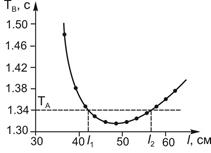
Рис. 4 Пример графика зависимости TВ(l)
6. Повторите п. 5, изменяя расстояние l в интервале от (l1 – 3) см до (l1 + 3) см с шагом в 1 см. Результаты занесите в таблицу 3.
Таблица 3
| l, см | l1 – 3 см | l1 – 2 см | … | l1 + 3 см |
| ТА, с | ||||
| ТВ, с |
7.
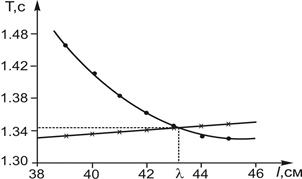 |
Постройте графики зависимостей ТА = f(l) и ТВ = f (l) на одном листе миллиметровой бумаги (рис.5). Приведенная длина маятника соответствует точке пересечения кривых (см. рис.5) l=λ, по этому графику определяют и период Т0, соответствующий этому расстоянию между втулками А и В. Установите опорную втулку В на расстоянии l=λ от втулки А, по-прежнему не меняя положения втулки А. Убедитесь, что период колебаний маятника на каждой опорной втулке соответствует Т0.
Рис. 5 Определение приведенной длины
оборотного маятника графическим способом
8. По формуле (14) рассчитайте ускорение свободного падения. Оцените погрешность, учитывая погрешности измерительных приборов, приведенные в таблице1.
9. Сравните периоды колебаний для физического и математического маятников, если длина математического маятника равна приведенной длине физического .
| <== предыдущая лекция | | | следующая лекция ==> |
| Порядок выполнения работы. Приборы: штатив, две ножки которого снабжены винтами, позволяющими установить прибор по имеющемуся на нём уровню так | | | определение модуля юнга методом изгиба |
Дата добавления: 2016-03-15; просмотров: 8458;
