Изучение прецессии гироскопа
Гироскопический эффект – поразительное явление динамики, которое позволяет объяснить, например, устойчивость вращающегося волчка, устойчивость велосипеда при вращении колес и т.п.
Понять гироскопический эффект можно только на основе законов вращательного движения тела. Напомним эти законы и рассмотрим суть явления.
Быстроту вращения тела относительно оси описывают угловой скоростью ω. Если за время dt, тело повернулось вокруг оси на угол dφ, то
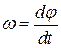 , (1)
, (1)
 т.е. это просто угол поворота за единицу времени (рад/c). Так как за один полный оборот происходит поворот тела на угол 2π радиан, то угловую скорость можно выразить через частоту вращения ν или период вращения T:
т.е. это просто угол поворота за единицу времени (рад/c). Так как за один полный оборот происходит поворот тела на угол 2π радиан, то угловую скорость можно выразить через частоту вращения ν или период вращения T:
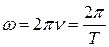
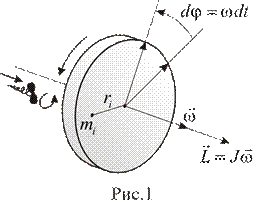
Чтобы характеризовать не только быстроту вращения, но и расположение оси вращения в пространстве, угловую скорость считают вектором 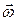 , направленным вдоль оси (по школьному правилу буравчика – рис.1).
, направленным вдоль оси (по школьному правилу буравчика – рис.1).
Для более полной характеристики состояния вращения следует еще учесть распределение массивных точек тела относительно оси. В динамике вращения тела вводят понятие – момент инерции тела J относительно оси:
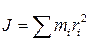 , (2)
, (2)
т.е. сумму масс всех точек тела, умноженных на квадраты их расстояний до оси вращения. Чем дальше массивные точки от оси, тем больше момент инерции всего тела (именно так делают особо инертные маховые колеса – маховики, у которых основная масса распределена по ободу колеса).
Самой полной характеристикой состояния вращения является величина, учитывающая и быстроту вращения, и распределение вращающихся масс. Она называется вектором момента импульса тела. Момент импульса тела относительно оси вращения равен произведению момента инерции тела на его угловую скорость:
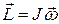 (3)
(3)
В соответствии с этим определением 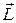 – вектор, также как и
– вектор, также как и 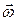 , направленный по оси. Если ось вращения в пространстве не закреплена, то тело с достаточно большим
, направленный по оси. Если ось вращения в пространстве не закреплена, то тело с достаточно большим 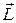 и представляет собой гироскоп.
и представляет собой гироскоп.
Понятно, что если нет никакого внешнего воздействия на вращающийся гироскоп (в том числе устранено трение), то он может вращаться бесконечно долго. При этом вектор момента импульса не изменяет ни величины, ни направления. В этом случае обычно говорят о законе сохранения момента импульса 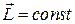 . (Свойство сохранения направления оси раскрученного гироскопа используется, в частности, в гирокомпасах).
. (Свойство сохранения направления оси раскрученного гироскопа используется, в частности, в гирокомпасах).
Однако если попытаться повернуть ось вращающегося гироскопа внешней силой, то происходит удивительной эффект – ось поворачивается совсем “не в ту сторону”! (Попытайтесь включенный пылесос наклонить “вправо” или “влево” – он при этом обязательно наклонится “вперед” или ”назад”).
Чтобы это понять, надо вспомнить, что внешнее динамическое воздействие при поворотах оказывается не силой, как в поступательном движении, а моментом силы. Так, если стержень массой m расположен вдоль оси OY (рис.2), то сила тяжести 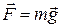 создает относительно закрепленной точки O момент силы M, который по известному из школы правилу равен произведению силы F на её плечо l:
создает относительно закрепленной точки O момент силы M, который по известному из школы правилу равен произведению силы F на её плечо l:
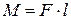 (4)
(4)
Момент силы M пытается повернуть стержень относительно центра O. Здесь l (плечо силы F) – кратчайшее расстояние от центра вращения до линии, вдоль которой действует сила.
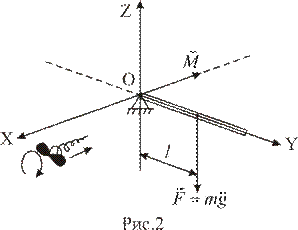 К этому определению следует добавить, что момент силы M создает не просто поворот стержня, а поворот вокруг конкретной оси OX в пространстве, поэтому момент силы условились считать вектором, направленным вдоль этой оси поворота OX по правилу буравчика (правилу винта): если буравчик вращать так, как сила
К этому определению следует добавить, что момент силы M создает не просто поворот стержня, а поворот вокруг конкретной оси OX в пространстве, поэтому момент силы условились считать вектором, направленным вдоль этой оси поворота OX по правилу буравчика (правилу винта): если буравчик вращать так, как сила 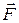 поворачивает стержень, то буравчик вкручивается против оси OX (см. вектор
поворачивает стержень, то буравчик вкручивается против оси OX (см. вектор 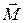 на рис.2). Итак, есть две важнейшие механические характеристики: момент импульса
на рис.2). Итак, есть две важнейшие механические характеристики: момент импульса 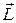 , описывающий состояние вращения тела и момент силы
, описывающий состояние вращения тела и момент силы 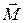 , описывающий внешнее динамическое воздействие на тело при его повороте под влиянием силы. Между ними существует простая связь, выражающая основной закон динамики вращения (уравнение моментов)
, описывающий внешнее динамическое воздействие на тело при его повороте под влиянием силы. Между ними существует простая связь, выражающая основной закон динамики вращения (уравнение моментов)
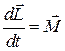 , (5)
, (5)
который говорит о том, что изменение вектора момента импульса тела за единицу времени (т.е. скорость изменения вектора L) равно вектору момента силы, действующей на это тело. Физический смысл его прост. Если внешнего воздействия нет ( 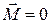 ), то
), то 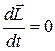 , и следовательно,
, и следовательно, 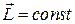 (гирокомпас, рассмотренный выше). Если внешнего воздействие есть (
(гирокомпас, рассмотренный выше). Если внешнего воздействие есть ( 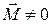 ), то состояние вращения изменяется, причем тем быстрее, чем больше воздействие
), то состояние вращения изменяется, причем тем быстрее, чем больше воздействие 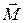 . Этот закон строго обосновывается в лекционном курсе физики.
. Этот закон строго обосновывается в лекционном курсе физики.
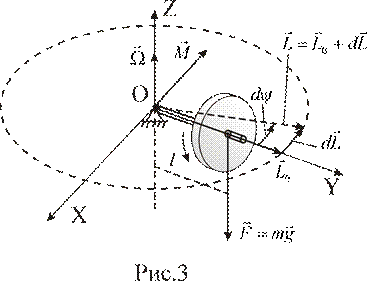
На основании уравнения моментов легко объяснить гироскопический эффект. Пусть гироскоп раскручен вокруг оси OY и обладает моментом импульса 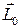 . Пусть ось гироскопа свободно опирается на упор в одной точке O (рис.3). Казалось бы, при этом сила тяжести
. Пусть ось гироскопа свободно опирается на упор в одной точке O (рис.3). Казалось бы, при этом сила тяжести 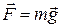 создает опрокидывающий момент
создает опрокидывающий момент 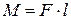 относительно точки O (т.е. относительно оси OX) и гироскоп должен падать. Однако этого не происходит.
относительно точки O (т.е. относительно оси OX) и гироскоп должен падать. Однако этого не происходит.
Дело в том, что согласно основному закону динамики вращения (5) изменение момента импульса 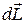 равно:
равно:
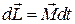 , (6)
, (6)
и, следовательно, направлено так же, как 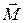 – в горизонтальной плоскости параллельно оси OX в сторону направления вектора
– в горизонтальной плоскости параллельно оси OX в сторону направления вектора 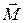 , т.е.
, т.е. 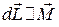 .
.
 В результате через время dt вектор
В результате через время dt вектор 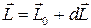 окажется в той же горизонтальной плоскости, но повернутым на угол dψ относительно
окажется в той же горизонтальной плоскости, но повернутым на угол dψ относительно 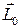 .
.
Таким образом, мы видим, что ось гироскопа не “опрокидывается” в вертикальной плоскости, а поворачивается в горизонтальной плоскости. Такое движение называется прецессией гироскопа. Итак, свободная ось гироскопа поворачивается в горизонтальной плоскости, т.е. вокруг неподвижной оси Z - оси прецессии. Это вращение на рис.3 можно изобразить вектором 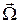 – вектором угловой скорости прецессии, направленным вдоль оси Z. Величину угловой скорости прецессии Ω легко получить из треугольника моментов импульсов (
– вектором угловой скорости прецессии, направленным вдоль оси Z. Величину угловой скорости прецессии Ω легко получить из треугольника моментов импульсов ( 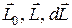 ) на рис.3:
) на рис.3:
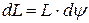 ,
,
где 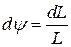 – угол поворота оси гироскопа, выраженный в радианах. Вместе с (6) это дает:
– угол поворота оси гироскопа, выраженный в радианах. Вместе с (6) это дает: 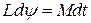 , откуда, учитывая, что
, откуда, учитывая, что 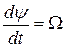 – угол прецессии в единицу времени, т.е. угловая скорость прецессии, получаем:
– угол прецессии в единицу времени, т.е. угловая скорость прецессии, получаем:
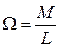 , или
, или 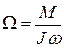 . (7)
. (7)
Таким образом, во-первых, угловая скорость прецессии гироскопа Ω тем меньше, чем больше угловая скорость ω вращения его вокруг собственной оси, и во-вторых, чем больше “опрокидывающий момент” М, тем больше Ω.
Экспериментальной задачей лабораторной работы и является проверка этих двух закономерностей: 1) 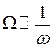 ; 2)
; 2) 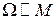 .
.
Дата добавления: 2016-03-15; просмотров: 1793;
