Общие принципы аналого-цифрового преобразования.

Аналого-цифровые и цифро-аналоговые преобразователи

В электронных системах одинаково широко используют обработку информации, представленной как в аналоговой, так и цифровой формах. Объясняется это тем, что первичная, исходная информация о различных физических величинах и процессах носит, как правило, аналоговый характер. Обработку же этой информации, в силу рассмотренных ранее причин, удобнее вести в цифровой форме. Использование полученных после цифровой обработки результатов также в большинстве случаев требует их аналогового представления. Следовательно, любая система, использующая цифровые методы обработки аналоговой информации, должна содержать устройства взаимного преобразования аналоговых и цифровых сигналов. Роль таких устройств выполняют аналого-цифровые и цифро-аналоговые преобразователи (АЦП и ЦАП).

Аналого-цифровой преобразователь - устройство, предназначенное для преобразования непрерывно изменяющейся во времени аналоговой физической величины в эквивалентные ей значения числовых кодов.

Цифро-аналоговый преобразователь - устройство, предназначенное для преобразования входной величины, представленной последовательностью числовых кодов, в эквивалентные им значения заданной физической величины.

Основной вопрос, с которым приходится сталкиваться при использовании АЦП и ЦАП, является вопрос адекватности полученного в результате преобразования сигнала исходному физическому процессу, т.е. вопрос точности преобразования. Поэтому рассмотрим алгоритмы этих преобразований с точки зрения погрешностей, возникающих при их выполнении.

Для простоты, в дальнейшем будем предполагать, что реальная физическая величина представлена уровнем напряжения, то есть будем рассматривать процесс преобразования уровня напряжения в числовой код и обратно.

Общие принципы аналого-цифрового преобразования.

Процесс преобразования аналоговой величины в цифровой аналог, как было показано во введении, состоит из трех этапов:

- квантования по времени;

- дискретизации по уровню;

- кодирования, то есть сопоставления полученных значений некоторым числовым эквивалентам.

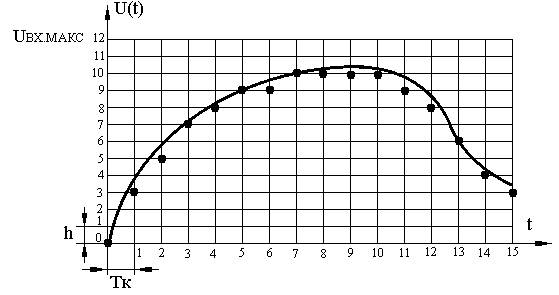
Рис.11.1. Временные диаграммы аналого-цифрового преобразования.

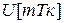На рис.11.1. приведены временные диаграммы, поясняющие принципы аналого-цифрового преобразования. Исходную аналоговую величину ( ) дискретизируют по времени, то есть выбирают конечное число значений , где m=0, 1, 2,… и Тк - период квантования по времени. При этом значения между моментами квантования теряются, но выбранные значения точно соответствуют реальным значениям в данные моменты времени. При выполнении определенных условий (условия теоремы Котельникова, согласно которой частота квантования должна быть больше удвоенной частоты преобразуемого сигнала или его наивысшей гармоники) по полученным значениям можно точно восстановить исходный сигнал. То есть ошибка преобразования на этом этапе отсутствует.

Далее полученные значения округляют до ближайшего значения, кратного шагу дискретизации по уровню h ( 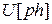),где p = 0, 1, 2,…. Таким образом, вместо бесконечного числа значений исходного аналогового сигнала, получаем конечное число его значений в заданные моменты времени. Очевидно, что связь выбранных значений ( 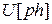) с реальными величинами исходной функции ( ) для каждого выбранного момента времени 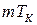определяется выражением:

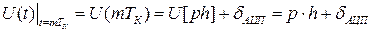, (11.1)

где: 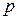- номер уровня и 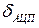- ошибка преобразования.

Значение 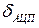определяется выбранным методом округления и в любом случае не превышает . Эту величину ( 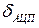) называют шумом квантования и она принципиально присуща самому методу аналого-цифрового преобразования. Уменьшение 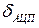связано с уменьшением величины h, то есть с увеличением допустимого числа уровней квантования 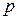. То есть на этапе квантования по уровню вносится ошибка, принципиально присущая рассматриваемому методу. Полагая в выражении 11.1 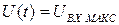и 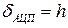получим зависимость максимального количества уровней квантования ( 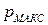) от максимально допустимого входного напряжения ( 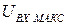) и шага квантования по уровню .

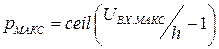или (11.2)

Теперь если каждому значению 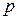сопоставить число (в простейшем случае это номер уровня), получим последовательность чисел, эквивалентных дискретным значениям функции. Полученная последовательность номеров уровней и образует совокупность числовых эквивалентов (кодов) значений аналоговой функции в последовательные моменты времени. Для функции, приведенной на рис.11.1, эта последовательность, выраженная в десятичной системе счисления, имеет вид: 0, 3, 5, 7, 8, 9, 9, 10, 10, 10, 10, 9, 8, 6, 4, 3. Таким образом, квантование исходного сигнала по уровню достигается округлением ее значений до конечного числа заданных дискретных уровней, а дискретизация по времени – последовательным формированием кодов, поставленных в соответствие этим значениям в дискретные моменты времени.

Переходя к двоичной системе счисления можно сказать, что разрядность двоичного числа ( 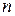), необходимая для отображения выбранного числа уровней определяется неравенством 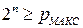. Тогда, с учетом 11.2. для разрядности двоичного кода получим:

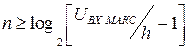, (11.3)

или при заданной разрядности 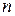определим максимальное значение шага квантования по уровню h:

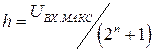. (11.4.)

Последнее выражение, при заданной разрядности двоичного кода, позволяет оценить погрешность АЦП преобразования (шум квантования).

Упражнение.11.1. При условии , что 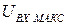= 5В и 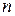=8, м определить выходной код АЦП для входного напряжения 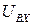= 3.25В

Решение.

- Для заданных условий определим величину шага квантования по уровню h. Согласно выражению 11.4 имеем 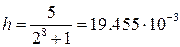В;

- Полагая в выражении 11.1. 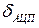= 0, найдем значение выходного кода p 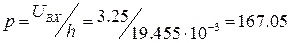. Отбрасываем дробную часть и получаем код 167₁₀ или 1010 0111₂ .

Упражнение.11.2. . Определить абсолютную ошибкупреобразования, выполненного в упражнении 11.1.

Решение.

- Выходное напряжение, соответствующее полученному коду равно ;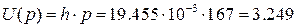

- Абсолютная погрешность преобразования 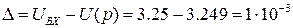В.

Упражнение.11.3. Для условий из упражнения 11.1 определить входное напряжение, соответствующее коду 0101 0110₂

Решение.

- Переведем заданный код в десятичную систему счисления:01010110₂ = 86₁₀ ;

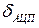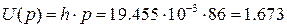- Входное напряжение найдем из выражения 11.1 с учетом, что = 0 В;

- Реальное входное напряжение может находиться в диапазоне 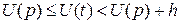,то есть 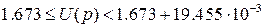В.

Все вышесказанное справедливо в случае, если диапазон преобразуемого в код напряжения определяется условием: 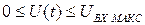. Если это условие не выполняется и 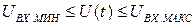, то в выражениях 11.2…..11.4. вместо 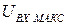необходимо использовать приведенное значение 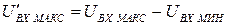, отображающее реальный диапазон преобразуемого напряжения.

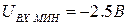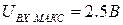Упражнение.11.4. При условии, что и определить код, соответствующий напряжению 1.5В.

Решение.

- Для заданных условий определим величину шага квантования по уровню h. Согласно выражению 11.4 имеем 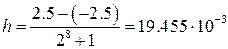В;

- Так как при заданных условиях код 0000 0000 соответствует напряжению -2.5В, то реально преобразуемое в код напряжение превышает эту величину на (2.5+1.5) В, то есть преобразуется в код напряжение 4 В;

- Полагая в выражении 11.1. 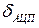= 0, найдем значение выходного кода p . Отбрасываем дробную часть и получаем код 205₁₀ или 1100 1101₂ .

Примечание. Отметим, что при заданном в примере диапазоне преобразуемого напряжения, нулевому входному напряжению соответствует код 1000 0000.

Упражнение.11.5. Для условий из упражнения 11.4 определить входное напряжение, соответствующее коду 0101 0110₂

Решение.

- Переведем заданный код в десятичную систему счисления:01010110₂ = 86₁₀ ;

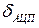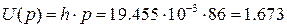- Расчетное входное напряжение найдем из выражения 11.1 с учетом, что = 0: В;

- Полученное значение является превышением напряжения над уровнем -2.5 В. Поэтому входное напряжение (измеренное относительно нулевого уровня) равно: 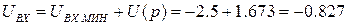В. Реальное входное напряжение может находиться в диапазоне 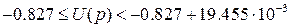В.