Лекция 3 Элементы механики сплошных сред. Упругие напряжения
План
1. Элементы механики сплошных сред. Стационарное движение идеальной жидкости. Уравнение Бернулли.
2. Упругие напряжения. Закон Гука.
Тезисы
1. Объем газа определяется объемом того сосуда, который газ занимает. В жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом. В механике с большой степенью точности жидкости и газы рассматриваются как сплошные, непрерывно распределенные в занятой ими части пространства. Плотность жидкости мало зависит от давления. Плотность же газов от давления зависит существенно. Из опыта известно, что сжимаемостью жидкости и газа во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости, плотность которой всюду одинакова и не изменяется со временем. Идеальная жидкость - физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения. Идеальная жидкость - воображаемая жидкость, в которой отсутствуют силы внутреннего трения.Ей противоречит вязкая жидкость. Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называетсядавлением ржидкости 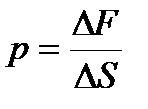 . Единица давления - паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2 (1 Па=1 Н/м2). Давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью.
. Единица давления - паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2 (1 Па=1 Н/м2). Давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью.
Давление изменяется линейно с высотой. Давление Р=rgh называется гидростатическим. Сила давления на нижние слои жидкости больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа) 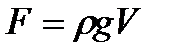 , где r — плотность жидкости, V — объем погруженного в жидкость тела.
, где r — плотность жидкости, V — объем погруженного в жидкость тела.
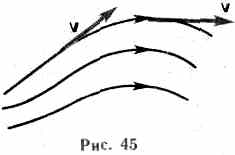
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). По картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
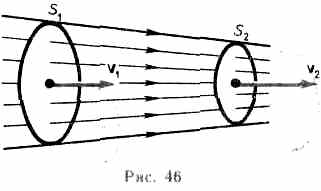
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 46). Если жидкость несжимаема (r=const), то через сечение S2пройдет за 1 с такой же объем жидкости, как и через сечение S1, т. е. 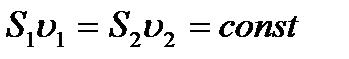 Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.
Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости. 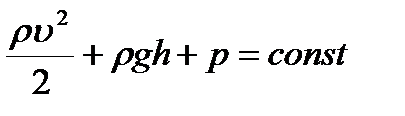 - уравнение Бернулли - выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости (здесь р - статическое давление (давление жидкости на поверхность обтекаемого ею тела), величина
- уравнение Бернулли - выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости (здесь р - статическое давление (давление жидкости на поверхность обтекаемого ею тела), величина 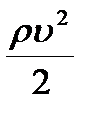 — динамическое давление,
— динамическое давление, 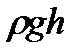 - гидростатическое давление). Для горизонтальной трубки тока уравнение Бернулли записывается в виде
- гидростатическое давление). Для горизонтальной трубки тока уравнение Бернулли записывается в виде 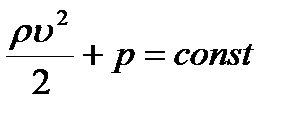 , где левая часть называется полным давлением. Формула Торичелли записывается:
, где левая часть называется полным давлением. Формула Торичелли записывается: 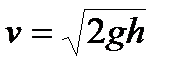
Вязкость - это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S, и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. Величина Dv/Dx показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направлению движения слоев, и называется градиентом скорости. Таким образом, модуль силы внутреннего трения равен 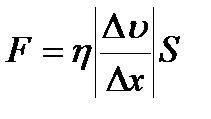 , где коэффициент пропорциональности h, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью). Единица вязкости — паскаль•секунда (Па•с) (1 Па•с=1 Н•с/м2). Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Методы определения вязкости:
, где коэффициент пропорциональности h, зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью). Единица вязкости — паскаль•секунда (Па•с) (1 Па•с=1 Н•с/м2). Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Методы определения вязкости:
1) формула Стокса 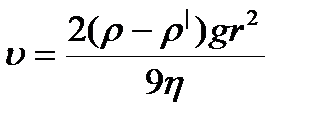 ; 2) формула Пуазейля
; 2) формула Пуазейля 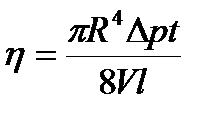
2. Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими. Сила, действующая на единицу площади поперечного сечения, называется напряжением 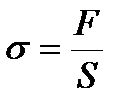 и измеряется в паскалях. Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Относительное изменение длины стержня (продольная деформация)
и измеряется в паскалях. Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Относительное изменение длины стержня (продольная деформация) 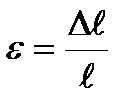 , относительное поперечное растяжение (сжатие)
, относительное поперечное растяжение (сжатие) 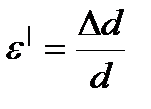 , где d -— диаметр стержня. Деформации e и e' всегда имеют разные знаки
, где d -— диаметр стержня. Деформации e и e' всегда имеют разные знаки 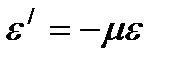 , где m — положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона.
, где m — положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона.
Роберт Гук экспериментально установил, что для малых деформаций относительное удлинение e и напряжение s прямо пропорциональны друг другу: 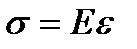 , где коэффициент пропорциональности Е – модуль Юнга.
, где коэффициент пропорциональности Е – модуль Юнга.
Модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице 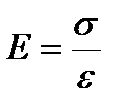 . Тогда закон Гука можно записать так
. Тогда закон Гука можно записать так 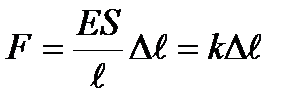 , где k — коэффициент упругости: удлинение стержня при упругой деформации пропорционально действующей на стержень силе. Потенциальная энергия упруго растянутого (сжатого) стержня
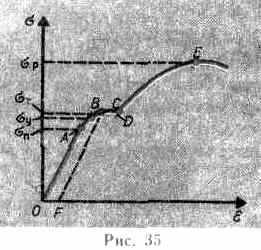
, где k — коэффициент упругости: удлинение стержня при упругой деформации пропорционально действующей на стержень силе. Потенциальная энергия упруго растянутого (сжатого) стержня 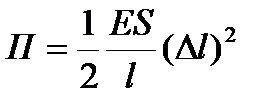 Деформации твердых тел подчиняются закону Гука только для упругих деформаций. Связь между деформацией и напряжением представляется в виде диаграммы напряжений (рис. 35). Из рисунка видно, что линейная зависимость s (e), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности (sп). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость s (e) уже не линейна) и до предела упругости (sу) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей — CF. Напряжение, при котором появляется заметная остаточная деформация (~=0,2 %), называется пределом текучести (sт) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения - предел прочности (sp).
Деформации твердых тел подчиняются закону Гука только для упругих деформаций. Связь между деформацией и напряжением представляется в виде диаграммы напряжений (рис. 35). Из рисунка видно, что линейная зависимость s (e), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности (sп). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость s (e) уже не линейна) и до предела упругости (sу) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей — CF. Напряжение, при котором появляется заметная остаточная деформация (~=0,2 %), называется пределом текучести (sт) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения - предел прочности (sp).
Дата добавления: 2016-03-10; просмотров: 996;
