Решение систем дифференциальных уравнений

Система MLимеет встроенные средства для решения обыкновенных дифференциальных уравнений (ДУ) любого порядка или систем ДУ. Дифференциальным уравнением n-го порядка называется соотношение вида F(t, y, y’,…, y⁽ⁿ⁾)=0. Наивысший порядок производной искомой функции в данном уравнении называется порядком дифференциального уравнения. Решением ДУ является такая функция, которая при подстановке в него обращает его в равенство. В случае системы дифференциальных уравнений n-го порядка решением являются n функций. При использовании численных методов решения искомые функции выражаются не аналитически, а в табличном виде (в виде набора значений в определенных точках). Самое простое ДУ – это уравнение 1-го порядка, разрешенное относительно производной. Оно имеет вид y’=f(t, y). ДУ и системы 2-го порядка и выше можно свести к системам 1-го порядка. Так, для того чтобы свести к системе 1-го порядка уравнение y’’=f(t, y, y’), нужно использовать замену: y₁=y и y₂=y’. В результате замены будем иметь систему

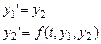
В ML имеется целый ряд встроенных функций, предназначенных для решения систем дифференциальных уравнений. Это функции ode23, ode45, ode113. В них реализованы различные методы решения обыкновенных ДУ. Наиболее часто используют функции ode23 и ode45, в основе работы которых лежит метод Рунге–Кутта. Для систем уравнений 2-го и 3-го порядков используют функцию ode23, а для систем 4-го и 5-го порядков – функцию ode45. Обращение к функции, находящей решение системы ДУ, имеет вид

[t, y]= <имя встроенной функции>(fun, interval, y0 ),

где fun – имя m-файла, в котором вычисляются правые части системы ДУ; interval – вектор, определяющий отрезок, на котором ищется решение; y0 – скаляр или вектор-столбец, в котором задаются начальные условия; t – вектор-столбец, содержащий значения независимой переменной на заданном интервале (обычно это время t); y – матрица решений. Количество столбцов в ней равно порядку системы ДУ. Каждый столбец содержит значения одной искомой функции на заданном отрезке. Каждая строка соответствует определенному значению t.

П р и м е р. Имеем ДУ 2-го порядка y’’+4y’+5y=0, описывающее движение точки в зависимости от времени. Требуется его решить на отрезке [0,5] с начальными условиями y(0)=3 и y’(0)= -5.

Выполним замену: y₁=y и y₂=y’, получим систему ДУ:

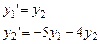
при y₁(0)=3 и y₂(0)=-5 (тогда y₁ будет обозначать координаты точки, а y₂ – ее скорость).

Составим файл-функцию для вычисления правых частей системы ДУ. Эта функция должна иметь два входных параметра: переменную t, вектор y с количеством элементов, равным числу неизвестных системы, и один выходной параметр (вектор правых частей системы):

function F=mydif(t,y)

F=[y(2); -5*y(1)-4*y(2)];

Сохраним файл с именем mydif в каталоге, разрешенном для записи. Обратимся к функции ode45:

>>[t,y]=ode45('mydif', [0 5],[3;-5])

В результате будут получены вектор-столбец t – вектор значений аргумента (в нашем примере это время) и матрица y из двух столбцов. Первый столбец содержит значения функции y₁, т.е. самой искомой функции при каждом значении t, а второй столбец – значения функции y₂, т.е. первой производной искомой функции.
У нас в первом столбце будут получаться значения координат точки, а во втором – значение скорости ее движения в каждый момент времени t.

Отобразим график решения ДУ и график производной (рис. 34):

>> plot(t,y(:, 1), 'r', t, y (:, 2),'k--')

>> xlabel('t');

>> ylabel('y')

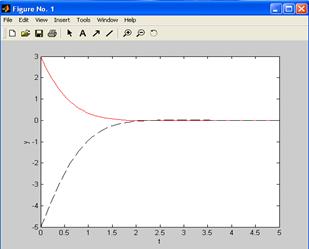
Рис. 34

Лабораторная работа №1

Знакомство с пакетом MAtlab,
решение простейших задач в системе MAtlab

Цель работы – познакомиться с интерактивным пакетом
Matlab 6.5, предназначенным для решения широкого круга инженерных и математических задач, научиться задавать векторы и матрицы, выполнять различные действия с ними, использовать встроенные функции для их обработки, а также изучить средства графического отображения результатов расчета и освоить создание скрипт-файлов.

Постановка задачи

1. Вычисление значений функции на заданном отрезке.

2. Выполнение действий с векторами.

3. Формирование и выполнение действия с матрицами.

4. Построение графиков функций одной переменной на заданном отрезке.

5. Построение графика функции двух переменных.

6. Создание скрипт-файла.

По результатам работы должен быть составлен отчет, содержащий тексты индивидуальных заданий, команды MLдля решения задач, текст script-файла, а также графическое представление результатов работы.