Концентрация напряжений.
При осевом растяжении или сжатии нормальные напряжения распределяются равномерно в поперечном сечении призматических стержней. Если же в стержне имеется отверстие или выточка, то напряжения в сечении распределяются неравномерно: около отверстия или выточек появляется повышенное напряжение.
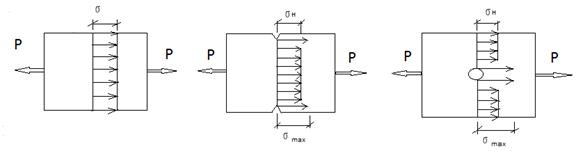
а =σmax/σ н – коэффициент концентрации напряжений.
σн = Р/Ан, где Ан (нетто) - площадь сечения в ослабленном месте.
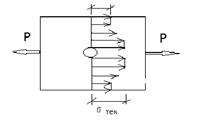
Концентрация напряжения опасна для хрупких материалов, а в пластичных материалах после достижения σmax=σтекучести, напряжения дальше не растут, а увеличиваются напряжения в других точках поперечного сечения.
Напряжения и деформации при действии равномерно распределенной осевой нагрузки
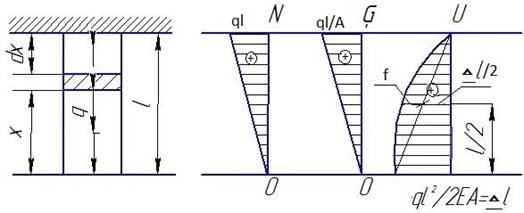
Найдем напряжение и деформации в начале для сечения находящегося на расстоянии x от свободного конца.

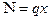 -сила
-сила
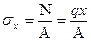
При x=0; N=0; 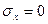
При X= 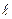 ;
; 
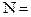 q
q 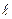 ;
; 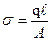
Переходим к определению деформаций.
Вначале найдем удлинение участка dx
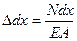 - закон Гука (собственным весом участка пренебрегаем).
- закон Гука (собственным весом участка пренебрегаем).
Удлинение участка ( 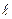 -x) получим если последнее выражение проинтегрируем от x до
-x) получим если последнее выражение проинтегрируем от x до 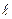
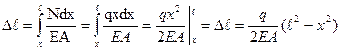 - удлинение участка (
- удлинение участка ( 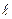 -x)
-x)
X=0 тогда 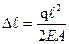
X= 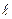 тогда
тогда 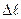 =0
=0
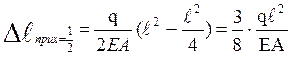
 f=
f= 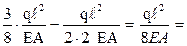 f –стрела параболы
f –стрела параболы
В свободном конце стержня перемещения можно определить по формуле
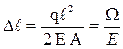
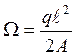 - площадь эпюры
- площадь эпюры 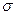 .
.
Если в качестве распределенной нагрузки служит плотность материала стержня 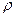 , то
, то 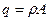
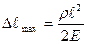 (умножим числитель и знаменатель на А).
(умножим числитель и знаменатель на А).
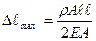
Пусть 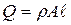 - собственный вес стержня.
- собственный вес стержня.
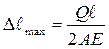 -деформация от собственного веса.
-деформация от собственного веса.
Ранее получили что при растяжении стержня силой Р деформации равны 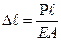 .
.
Вывод: как видно деформации от собственного веса стержня получаются в 2 раза меньше деформации от силы Р.
Опытное изучение растяжение материалов. Диаграммы напряжений
Механические свойства материалов выявляются при испытании их под нагрузкой. Наиболее распространенным видом испытаний являются испытания на растяжение. Это объясняется тем, что мех. свойства мат-лов полученные при испытании на растяжение во многих случаях позволяют достаточно полно судить о поведении материалов при других видах деформации. С другой стороны испытания на растяжении легко осуществимы.
Для испытаний берут образцы стандартных размеров

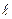 -общая длина образца
-общая длина образца
Для стандартных образцов 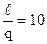
Чаще всего испытывают образцы диаметром d=1см. Испытания осуществляют на специальных испытательных машинах. Многие машины автоматически вычерчивают графики зависимости нагрузки от деформации.
Ниже рассмотрим диаграмму растяжения малоуглеродистой стали.
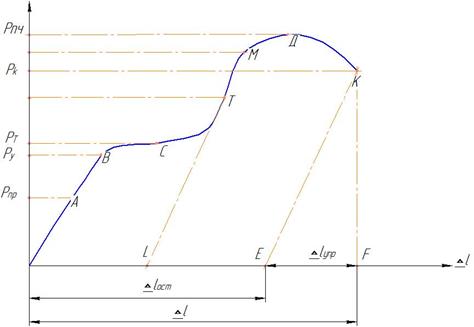
Рассмотрим характерные участки и точки этой диаграммы.
На участке ОА деформации растут пропорционально нагрузкам, следовательно до точки А справедлив закон Гука. Точка А соответствует пределу пропорциональности
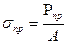 - предел пропорциональности.
- предел пропорциональности.
На участке АВ линейная зависимость между Р и 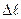 нарушается. Однако до точки В возникают в образце упругие деформации. Это означает, если образец нагрузить до точки В, а затем разгрузить, то деформации в образце исчезнут (образец примет первичную форму
нарушается. Однако до точки В возникают в образце упругие деформации. Это означает, если образец нагрузить до точки В, а затем разгрузить, то деформации в образце исчезнут (образец примет первичную форму 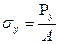 - предел упругости.
- предел упругости.
В окрестности точки С имеется почти горизонтальная площадка, здесь деформации растут без видимого увеличения нагрузки. Эта площадка называется площадкой текучести. На поверхности образца появляются наклонные линии. Впервые эти линии заметил русский металлург Чернов. Независимо от него так же заметил Людекс. (Линии Людекса-Чернова)
Точка С – соответствует пределу текучести.
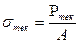 - предел текучести
- предел текучести
За площадкой текучести для дальнейшего деформирования образца необходимо увеличить нагрузку.
Точка D – соответствует пределу прочности.
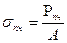 - предел прочности (временного сопротивления).
- предел прочности (временного сопротивления).
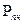 - наибольшая нагрузка, которую образец выдержал при испытаниях.
- наибольшая нагрузка, которую образец выдержал при испытаниях.
Начиная с точки D в образце появляется шейка (местное сужение).
На участке DK деформации растут в районе шейки.
В точке К образец разрушается
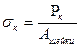 , где
, где 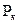 - напряжение в момент разрушения.
- напряжение в момент разрушения.
А – площадь поперечного сечения шейки в момент разрушения.
КЕ || ОА
На участке ОЕ возникают остаточные деформации 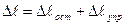

Замечания:
1) Если образец нагрузить до точки Т, а затем разгрузить, то диаграмма пойдет по линии
TL || OA. При повторном нагружении этого образца карандаш пойдет по линии LTDK.
Как видно в этом случае площадка текучести исчезнет и упругие свойства материала возрастают. Это явление называется наклепоми широко используется в строительстве.
Например арматуру железо-бетонных конструкций предварительно напрягают.
2) Если после разгрузки дать образцу возможность «отдохнуть» (не менее 100 часов) , то при повторном нагружении диаграмма пойдет по линии LTM. Это явление называется явлением старения.
По результатам испытаний можно судить о прочности упругости и пластичности материала.
Прочностьхарактеризуется величинами 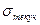 и
и 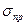
Упругостьхарактеризуется 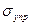
Пластичностьхарактеризуется 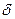 и
и 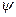
Где 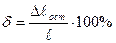 - остаточное относительное удлинение
- остаточное относительное удлинение
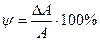 - относительное сужение.
- относительное сужение.
Где 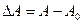 , А – площадь поперечного сечения до деформации,
, А – площадь поперечного сечения до деформации, 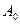 -площадь после деформации.
-площадь после деформации.
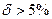 - для пластичного материала
- для пластичного материала
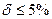 - для хрупких материалов
- для хрупких материалов
Диаграмма напряжений.
Рассмотренная в предыдущем параграфе диаграмма растяжения зависит от размеров образца. Для того чтобы исключить влияние размеров образца на форму диаграммы иногда ее представляют в координатах 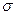 и
и 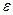
Ниже рассмотрим диаграммы напряжений для некоторых материалов
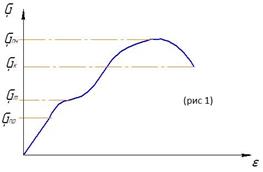
tg 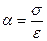
Из закона Гука известно
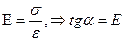 - модуль упругости
- модуль упругости
Диаграмма напряжения хрупкого материала (чугун)

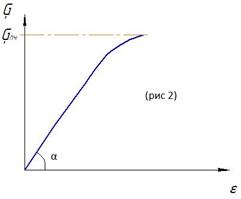
Как видно из рис.2 для хрупких материалов площадка текучести отсутствует, следовательно нет предела текучести. Также видно, что хрупкие материалы при растяжении разрушаются при малых деформациях
Диаграмма растяжения бетона
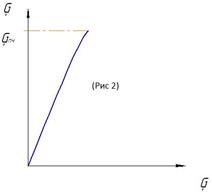
Испытание на сжатие
Для изучения поведения материалов при сжатии изготавливают образцы цилиндрической формы (для металлов).
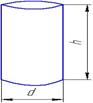
Для испытание бетона, камня, дерева берут образцы призматической формы
(для бетона) 20х20х20 для раствора 7,07х7,07х7,07
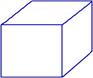
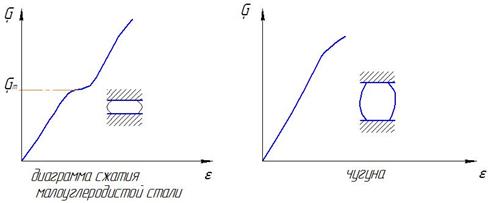
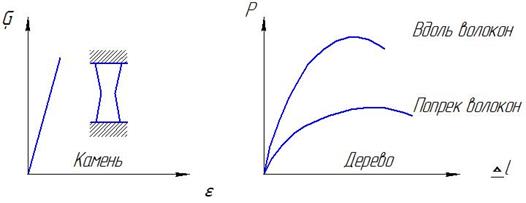
Как видно из рисунков, малоуглеродистая сталь до предела текучести на сжатие работает так же как и при растяжении.
Предел текучести при сжатии примерно равняется пределу текучести при растяжении.
σсжтек=σ расттек ; 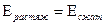
Малоуглеродистая сталь при сжатии не разрушается, образец превращается в диск (нет предела прочности).
Хрупкие материалы: чугун, бетон и т. д на сжатие работают лучше, чем на растяжение, например предел прочности на сжатие чугуна примерно в 4 раза больше предела прочности при растяжении, а у бетона в 8-10 раз.
Расчет прочности при растяжении и сжатии.
Дата добавления: 2016-02-13; просмотров: 1938;
