Уравнение проекции Меркатора
Покажем, что прямая линия на карте в меркаторской проекции действительно представляет собой локсодромию.
Локсодромия ® кривая, пересекающая все меридианы под одним и тем же углом К (рис. 6.2).
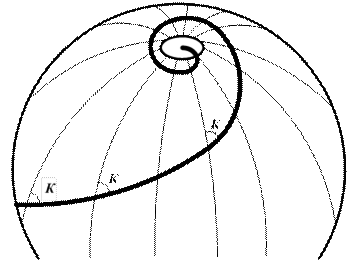
Рис. 6.2. Локсодромия на земном шаре
Судно, совершающее плавание постоянным курсом, перемещается именно по локсодромии.
Уравнение локсодромии на поверхности эллипсоида имеет вид:
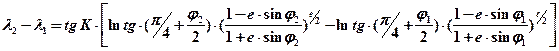 (6.6)
(6.6)
Если пренебречь сжатием эллипсоида и приняв Землю за шар, то уравнение локсодромии примет вид:
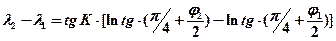 (6.7)
(6.7)
Из формулы (6.7) выводятся следующие свойства локсодромии:
· – при К = 0°(180°) ® локсодромия совпадает с меридианом;
- – при К = 90°(270°) ® локсодромия совпадает с параллелью, а при j = 0° – с экватором;
- – при любых других К – локсодромия является логарифмической спиралью, стремящейся к полюсу, но никогда его не достигающей;
- – локсодромия своей выпуклостью обращена к экватору.
Длину и направление локсодромии по известным координатам точек вычисляют по формулам аналитического счисления.
Напишем уравнение прямой, проходящей через т. А (Х0, У0) наклонно к оси Х под углом К равным курсу (рис. 6.3).
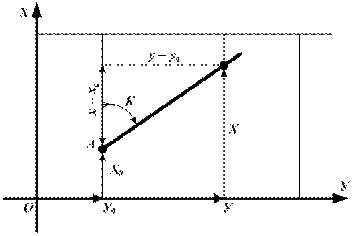
Рис. 6.3. Уравнение прямой
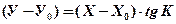 (6.8)
(6.8)
Подставим в полученное уравнение (6.5) вместо Х и У их выражения через j и l, принимая для простоты Землю за шар:
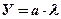 (6.9)
(6.9)
где а – коэффициент пропорциональности определяющий расстояния между меридианами.
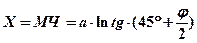 (6.10)
(6.10)
Тогда:
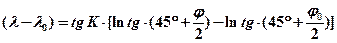 (6.11)
(6.11)
Это уравнение показывает, что прямая линия на меркаторской проекции действительно представляет собой локсодромию.
Таким образом, проводя на меркаторской проекции параллели в расстоянии МЧ от экватора, удовлетворяются оба требования, предъявляемые к морской навигационной карте.
Дата добавления: 2016-02-27; просмотров: 981;
