Понятия и определения.
Жидкость– собственно жидкость, газы и пары. При выводе основных законов вводят понятие идеальной жидкости.Предполагается, что идеальная жидкость (далее и.ж.) абсолютно не сжимаема, не изменяет плотности при изменении внешних условий, не обладает вязкостью.
Реальные жидкости: капельные и упругие.
Капельные– собственно жидкости. Практически не сжимаемы, не изменяют объема при нагревании.
Упругие – газы и пары – существенно меняют плотность и объем при изменении внешних условий.
Некоторые физические свойства жидкостей.
1.Плотность
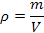
[ρ]=[кг/м3]
2.Уднльный вес – вес единицы объема
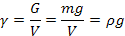
[γ]=[Н/м3]
3.
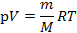
Плотность любого газа:
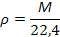
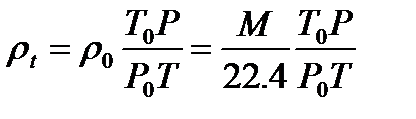
Как правило имеем дело со смесью газов. ρсм находится по правилу аддитивности:
ρсм=ρ1y1+ρ2y2+……………………………
yi – мольная доля
ЛЕКЦИЯ 3.
Вязкость.
При движении реальных жидкостей или газов в них возникают силы внутреннего трения, которые оказывают сопротивление движению потока. Свойство жидкости или газа оказывать сопротивление усилиям, вызывающим относительное перемещение частиц, называется вязкость.
Материальный поток в виде жидкости или газа движется слоями:
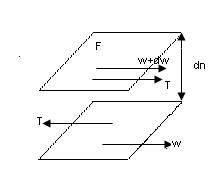
За счет разности скоростей движения слоев возникает касательная сила, которую нужно приложить , чтобы относительно сдвинуть эти слои.
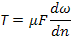
Величина Т пропорциональна поверхности контакта слоев F и отношению приращения величины скорости к расстоянию между слоями.
μ – коэффициент пропорциональности – динамический коэффициент вязкости (динамическая вязкость).
Сила сопротивления сдвигу – напряжение внутреннего трения.
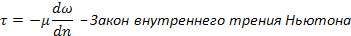
Напряжение внутреннего трения, возникающие между слоями жидкости, пропорционально градиенту скорости.
В системе единиц СГС вязкость измеряется в пуазах (П) или сантипуазах (сП). Единица динамической вязкости в системе СИ в Па·с. Пересчетная формула: 1 Па·с = 103 сП.
Динамическая вязкость – справочная величина.
Кинематическая вязкость n связана с динамической вязкостью соотношением:
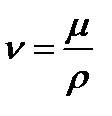
В системе СГС единица кинематической вязкости 1 стокс (ст), в системе СИ 1 м2/с; пересчетная формула: 1 м2/с = 104 ст.
Вязкость зависит от температуры, причем, для капельных жидкостей повышение температуры приводит к снижению вязкости, для газов при повышении температуры вязкость возрастает.
Те жидкости, которые подчиняются закону Ньютона, называются ньютоновскими.
Вязкость газов на практике – вязкость смеси.
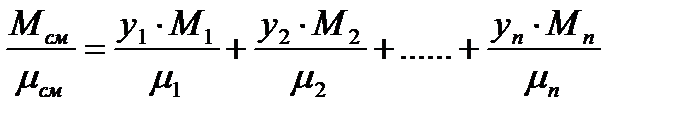 ,
,
| где m1 ,m2 … mn - | вязкость компонентов смеси, Па·с; |
| mсм - | вязкость смеси газов, Па·с; |
| М1 ,М2…Мn , Мсм - | молекулярная масса компонентов смеси и самой смеси, кг/кмоль; |
| у1 , у2 …уn - | объемная или мольная доля компонентов; |
| Мсм - | молекулярная масса смеси газов, г/моль. |
Молекулярная масса смеси газов рассчитывается по формуле:
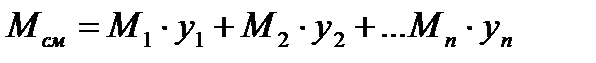
Вязкость газа при любой температуре находится по уравнению Сутерленда.
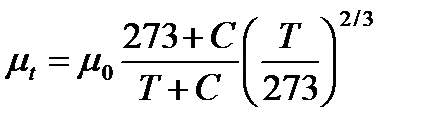 ,
,
| где m0 - | вязкость при нормальных условиях (обычно берется из справочной литературы); |
| С - | константа Сутерленда |
| T - | абсолютная температура, К. |
Гидростатика.
Давление.
Жидкость оказывает давление на дно и стенки сосуда, в котором она находится, а также на поверхность погруженного в нее тела.
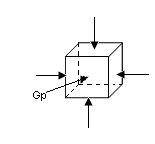

Сила давления будет оказывать влияние по всем трем направлениям и направлена по нормали к площадке, на которую она действует. Давление в любой точке жидкости одинакого по всем направлениям (в противном случае происходило бы перемещение жидкости) и направлено по нормали к площадке, на которую оно действует.
В системе СИ давление измеряется в паскалях (Па).
1 Паскаль (Па) = 1 н/м2. В системе МКГСС давление измеряется в кгс/м2. Давление можно также выражать в метрах столба жидкости, что связано с методами измерения давления. Пересчетная формула:
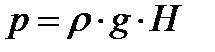 ,
,
| где р - | давление в паскалях, Па; |
| r - | плотность жидкости, кг/м3; |
| g - | ускорение свободного падения, м/с2; |
| Н - | высота столба жидкости в метрах, м. |
Разнообразные единицы давления и формулы для их пересчета приведены в литературе. Приведем наиболее важные расчетные соотношения:
1 атм (физическая) = 1,013 ·105 Па = 10 м вод.ст.=1,033 кгс/см2 = 760 мм рт.ст.
1 ат (техническая) = 9,81·104 Па = 10 м вод.ст. = 1кгс/см2 = 735 мм рт.ст.
1 мм вод.ст = 9,81 Па; 1 мм рт.ст = 133,3 Па.
1бар=105Па.
Наиболее часто давление измеряют дифференциальными манометрами, которые представляют собой U-образную стеклянную трубку, заполненную рабочей жидкостью (вода, спирт, ртуть). Один конец трубки находится внутри аппарата или устройства, а второй открытый конец связан с атмосферой. Рассмотрим две возможные ситуации.
В первом случае, когда столб жидкости в левом колене трубки ниже, чем в правом, в аппарате создается избыточное давление и именно его измеряет манометр. Разность уровней жидкости в левом и правом коленах соответствует разности:
Dр = (ратм + ризб) – ратм = ризб
| Аппарат ратм – рразр |
| Аппарат ратм + ризб |
| Рат |
| Рат |
| Dр = ризб |
| Dр = рразр |
Во втором случае столбик жидкости в левом колене выше, чем в правом, ратм выше, чем давление в аппарате. Тогда
Dр = ратм - (ратм - рразр) = рразр
Отсюда важный вывод: манометр никогда не показывает истинное (абсолютное) давление в аппарате, а показывает либо избыточное давление (то есть сверх атмосферного), либо разряжение (то есть недостающее до атмосферного давления).
Таким образом, для получения абсолютного давления в аппарате в первом случае к атмосферному добавляется избыточное давление, измеренное манометром, т.е.
рабс = ратм + ризб ,
а во втором случае
рабс = ратм – рразр.
Если в условиях задачи приводится избыточное давление, либо разряжение, значит для получения истинного абсолютного давления их необходимо пересчитать.
В гидростатике рассматривается равновесие жидкостей, находящихся в покое, при котором в жидкости отсутствует перемещение слоев относительно друг друга. В этом случае жидкости могут быть рассмотрены как идеальные.
Покой бывает: относительный и абсолютный.
Независимо от вида покоя на жидкость действуют сила давления и сила тяжести.
Зависимость между силами, действующими на жидкость, находящуюся в состоянии покоя, и определяющими условия равновесия жидкости, выражается дифференциальными уравнениями Эйлера.
Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем жидкости, находящийся в равновесии, равно нулю. В противном случае происходило бы перемещение жидкости.
Ось z:
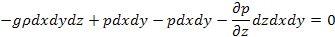
-gdm Аналогично записываем проекции сил по всем осям
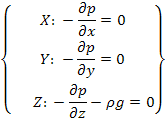
Эти уравнения показывают, что давление в покоящейся жидкости изменяется только по вертикали, остальное одинаково в любой точке горизонтальной плоскости; изменение по оси X и Y равны нулю.
Для получения закона распределения давления во всем объеме покоящейся жидкости следует проинтегрировать данную систему уравнений, интегралом которой является основное уравнение гидростатики.
ЛЕКЦИЯ 4.
Дата добавления: 2016-02-27; просмотров: 1838;
